2.4.1平面向量的物理背景及其含义
文档属性
| 名称 | 2.4.1平面向量的物理背景及其含义 |  | |
| 格式 | zip | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-07 10:46:14 | ||
图片预览






文档简介
课件23张PPT。2.4.1 平面向量数量积的物理背景及其含义 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作(1)理解和掌握向量数量积的定义;
(2)理解向量数量积的几何意义;
(3)掌握向量数量积的运算律;
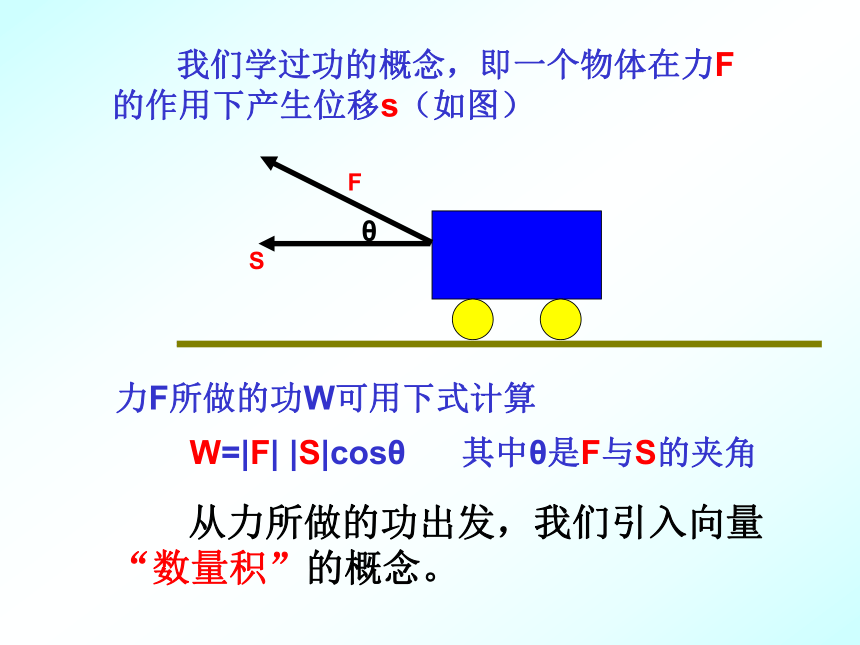
(4)掌握向量数量积的重要性质.数乘向量运算律两个向量的夹角的范围:复习: 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θFS力F所做的功W可用下式计算
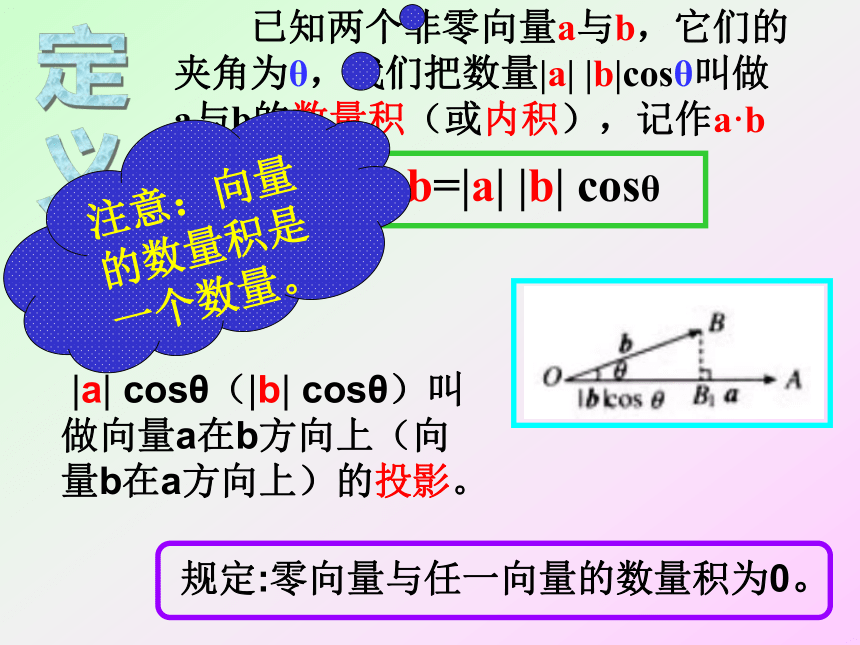
W=|F| |S|cosθ 其中θ是F与S的夹角 从力所做的功出发,我们引入向量“数量积”的概念。定
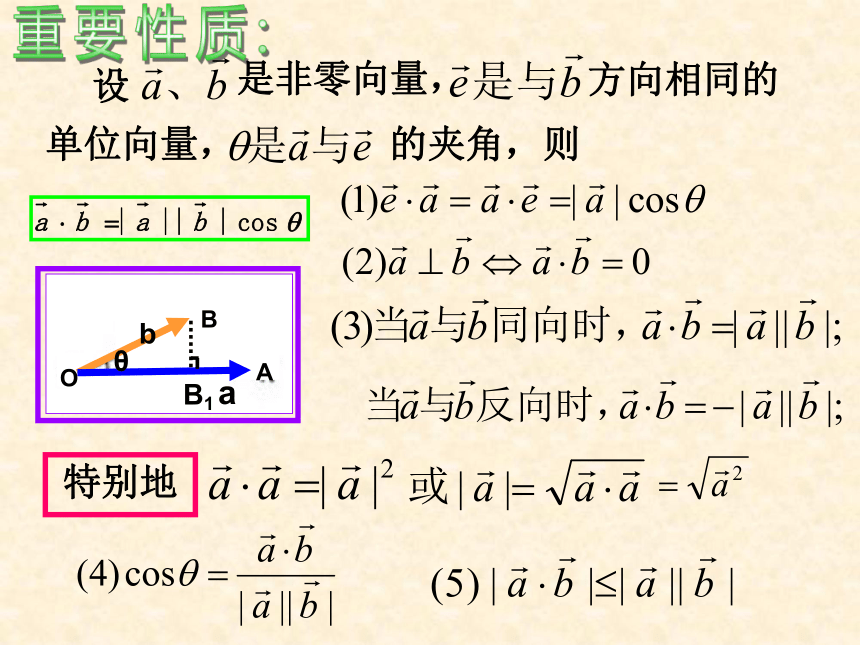
义 |a| cosθ(|b| cosθ)叫做向量a在b方向上(向量b在a方向上)的投影。注意:向量的数量积是一个数量。思考:a·b=|a| |b| cosθ当0°≤θ < 90°时a·b为正;当90°<θ ≤180°时a·b为负。当θ =90°时a·b为零。重要性质:特别地练习:1.若a =0,则对任一向量b ,有a · b=0.2.若a ≠0,则对任一非零向量b ,有a · b≠0.3.若a ≠0,a · b =0,则b=04.若a · b=0,则a · b中至少有一个为0.5.若a≠0,a · b= b · c,则a=c6.若a · b = a · c ,则b≠c,当且仅当a=0 时成立.√×××××√解:a·b = |a| |b|cosθ= 5×4×cos120°
=5×4×(-1/2)= -10例1 已知|a|=5,|b|=4,a与b的夹角θ=120°,求a·b。例2 已知a=(1,1),b=(2,0),求a·b。解: |a| =√2, |b|=2, θ=45 °
∴ a·b=|a| |b|cosθ= √2×2×cos45 °
= 2a·b的几何意义:二、平面向量的数量积的运算律:数量积的运算律:注: 则
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c . ONMa+bbac 向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 证明运算律(3)例 3:求证:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(1)(a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.证明:(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
=a2-b2.走进高考1、(2010广东)若向量 , ,
满足条件 ,则 ( )
(A)3 (B)4 (C)5 (D)6
2、(2009海南)已知 , ,向量 与 垂直,则实数λ的值为( )
(A) (B) (C) (D)BA解:解: 平面向量的数量积及其几何
意义;
2. 平面向量数量积的重要性质
及运算律;
3. 向量垂直的条件.课堂小结作业:1.第108页A组第6,7,8题
2.B组1,3题补充练习:3、用向量方法证明:直径所对的圆周角为直角。如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°分析:要证∠ACB=90°,只须证向
量 ,即 。解:设
则 ,
由此可得:
高中数学老师欧阳文丰制作(1)理解和掌握向量数量积的定义;
(2)理解向量数量积的几何意义;
(3)掌握向量数量积的运算律;
(4)掌握向量数量积的重要性质.数乘向量运算律两个向量的夹角的范围:复习: 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θFS力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角 从力所做的功出发,我们引入向量“数量积”的概念。定
义 |a| cosθ(|b| cosθ)叫做向量a在b方向上(向量b在a方向上)的投影。注意:向量的数量积是一个数量。思考:a·b=|a| |b| cosθ当0°≤θ < 90°时a·b为正;当90°<θ ≤180°时a·b为负。当θ =90°时a·b为零。重要性质:特别地练习:1.若a =0,则对任一向量b ,有a · b=0.2.若a ≠0,则对任一非零向量b ,有a · b≠0.3.若a ≠0,a · b =0,则b=04.若a · b=0,则a · b中至少有一个为0.5.若a≠0,a · b= b · c,则a=c6.若a · b = a · c ,则b≠c,当且仅当a=0 时成立.√×××××√解:a·b = |a| |b|cosθ= 5×4×cos120°
=5×4×(-1/2)= -10例1 已知|a|=5,|b|=4,a与b的夹角θ=120°,求a·b。例2 已知a=(1,1),b=(2,0),求a·b。解: |a| =√2, |b|=2, θ=45 °
∴ a·b=|a| |b|cosθ= √2×2×cos45 °
= 2a·b的几何意义:二、平面向量的数量积的运算律:数量积的运算律:注: 则
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c . ONMa+bbac 向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 证明运算律(3)例 3:求证:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(1)(a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.证明:(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
=a2-b2.走进高考1、(2010广东)若向量 , ,
满足条件 ,则 ( )
(A)3 (B)4 (C)5 (D)6
2、(2009海南)已知 , ,向量 与 垂直,则实数λ的值为( )
(A) (B) (C) (D)BA解:解: 平面向量的数量积及其几何
意义;
2. 平面向量数量积的重要性质
及运算律;
3. 向量垂直的条件.课堂小结作业:1.第108页A组第6,7,8题
2.B组1,3题补充练习:3、用向量方法证明:直径所对的圆周角为直角。如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°分析:要证∠ACB=90°,只须证向
量 ,即 。解:设
则 ,
由此可得:
