高中数学人教A版(2019)必修 第一册 第二章 二次函数与一元二次方程、不等式 课件(共24张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修 第一册 第二章 二次函数与一元二次方程、不等式 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 633.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 21:17:15 | ||
图片预览







文档简介
(共24张PPT)
二次函数与一元二次方程、不等式
课程目标
1.通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系。
2.使学生能够运用二次函数及其图像,性质解决实际问题。
3.渗透数形结合思想,进一步培养学生综合解题能力。
数学学科素养
1.数学抽象:一元二次函数与一元二次方程,一元二次不等式之间的联系;
2.逻辑推理:一元二次不等式恒成立问题;
3.数学运算:解一元二次不等式;
4.数据分析:一元二次不等式解决实际问题;
5.数学建模:运用数形结合的思想,逐步渗透一元二次函数与一元二次方程,一元二次不等式之间的联系。
自主预习,回答问题
阅读课本,思考并完成以下问题:
1.二次函数与一元二次方程、不等式的解的对应关系。
2.解一元二次不等方的步骤?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
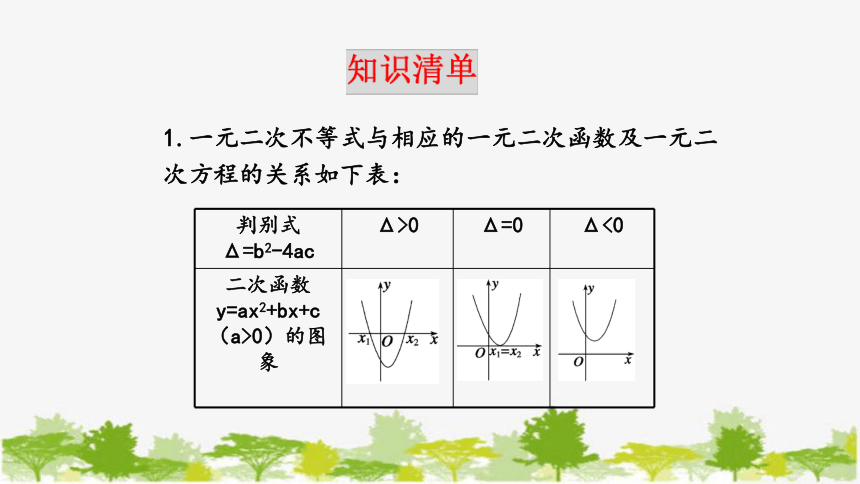
1.一元二次不等式与相应的一元二次函数及一元二
次方程的关系如下表:
判别式 Δ=b2-4ac Δ>0 Δ=0 Δ<0
二次函数 y=ax2+bx+c (a>0)的图象
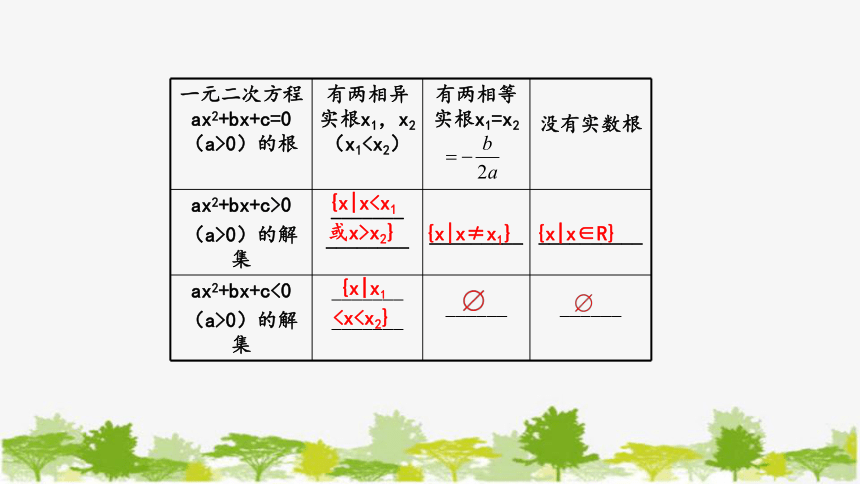
一元二次方程 ax2+bx+c=0 (a>0)的根 有两相异 实根x1,x2 (x1没有实数根
ax2+bx+c>0 (a>0)的解集 _______
________ _________
__________
ax2+bx+c<0 (a>0)的解集 _______ _______ ______ ______
{x|x≠x1}
{x|x∈R}
{x|x或x>x2}
{x|x1
2.一元二次不等式ax2+bx+c>0(a>0)的求解的算法。
(1)解ax2+bx+c=0;
(2)判断开口方向;
(3)根据开口方向和两根画草图;
(4)不等式>0,看草图上方,写对应x的结果;
不等式<0,看草图下方,写对应x的结果。
答案:D
1.
2.
答案:B
3.
答案:C
题型分析举一反三
题型一解不等式
解题方法(解不等式)
(1)解ax2+b+c=0;
(2)判断开口x方向;
(3)根据开口方向和两根画草图;
(4)不等式>0,看草图上方,写对应x的结果;
不等式<0,看草图下方,写对应x的结果。
题型二一元二次不等式恒成立问题
例2:(1)
解:
(2)
解:
解题方法(一元二次不等式恒成立问题)
[跟踪训练二]
1.
解:
2.
解:
解题方法(一元二次不等式实际应用问题)
(1)根据题意列出相应的一元二次函数;
(2)由题意列出相应一元二次不等式;
(3)求出解集;
(4)结合实际情况写出最终结果。
1.用可围成32m墙的砖头,沿一面旧墙(旧墙足够长)围成猪舍四间(面积大小相等的长方形)。应如何围才能使猪舍的总面积最大?最大面积是多少?
解:
人教A版必修第一册
谢 谢
二次函数与一元二次方程、不等式
课程目标
1.通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系。
2.使学生能够运用二次函数及其图像,性质解决实际问题。
3.渗透数形结合思想,进一步培养学生综合解题能力。
数学学科素养
1.数学抽象:一元二次函数与一元二次方程,一元二次不等式之间的联系;
2.逻辑推理:一元二次不等式恒成立问题;
3.数学运算:解一元二次不等式;
4.数据分析:一元二次不等式解决实际问题;
5.数学建模:运用数形结合的思想,逐步渗透一元二次函数与一元二次方程,一元二次不等式之间的联系。
自主预习,回答问题
阅读课本,思考并完成以下问题:
1.二次函数与一元二次方程、不等式的解的对应关系。
2.解一元二次不等方的步骤?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
1.一元二次不等式与相应的一元二次函数及一元二
次方程的关系如下表:
判别式 Δ=b2-4ac Δ>0 Δ=0 Δ<0
二次函数 y=ax2+bx+c (a>0)的图象
一元二次方程 ax2+bx+c=0 (a>0)的根 有两相异 实根x1,x2 (x1
ax2+bx+c>0 (a>0)的解集 _______
________ _________
__________
ax2+bx+c<0 (a>0)的解集 _______ _______ ______ ______
{x|x≠x1}
{x|x∈R}
{x|x
{x|x1
(1)解ax2+bx+c=0;
(2)判断开口方向;
(3)根据开口方向和两根画草图;
(4)不等式>0,看草图上方,写对应x的结果;
不等式<0,看草图下方,写对应x的结果。
答案:D
1.
2.
答案:B
3.
答案:C
题型分析举一反三
题型一解不等式
解题方法(解不等式)
(1)解ax2+b+c=0;
(2)判断开口x方向;
(3)根据开口方向和两根画草图;
(4)不等式>0,看草图上方,写对应x的结果;
不等式<0,看草图下方,写对应x的结果。
题型二一元二次不等式恒成立问题
例2:(1)
解:
(2)
解:
解题方法(一元二次不等式恒成立问题)
[跟踪训练二]
1.
解:
2.
解:
解题方法(一元二次不等式实际应用问题)
(1)根据题意列出相应的一元二次函数;
(2)由题意列出相应一元二次不等式;
(3)求出解集;
(4)结合实际情况写出最终结果。
1.用可围成32m墙的砖头,沿一面旧墙(旧墙足够长)围成猪舍四间(面积大小相等的长方形)。应如何围才能使猪舍的总面积最大?最大面积是多少?
解:
人教A版必修第一册
谢 谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
