华师大版 八年级上册 12.5因式分解 小结 课件(共17张PPT)
文档属性
| 名称 | 华师大版 八年级上册 12.5因式分解 小结 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-30 08:34:20 | ||
图片预览






文档简介
(共17张PPT)
因式分解
复 习 课
1.能灵活运用幂的运算性质、整式乘除、乘法公式等知识解决问题.
2.知道提公因式法、运用公式法分解因式的方法,能选择合适的方法分解因式.
3.感受数学与现实生活的密切联系,学会用类比、转化的数学思想与方法.
4.重点:整式的概念,整式加减运算,幂的运算性质,整式乘除运算,乘法公式的综合运用.
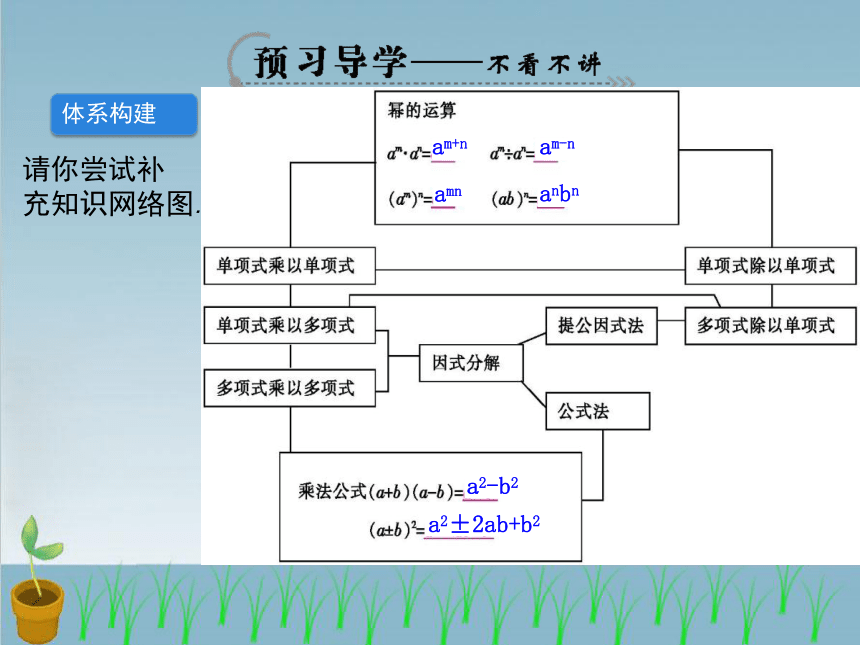
体系构建
请你尝试补
充知识网络图.
am+n
am-n
amn
anbn
a2-b2
a2±2ab+b2
核心梳理
1.幂的运算性质:
(1)同底数幂的乘法性质:am·an= (m,n都是正整数),即同底数幂相乘,底数不变,指数相加.
(2)同底数幂的除法性质:am÷an= (a≠0,m,n都是正整数,且m>n),即同底数幂相除,底数不变,指数相减.
(3)幂的乘方的性质:(am)n= (m,n都是正整数),即幂的乘方,底数不变,指数相乘.
(4)积的乘方的性质:(ab)n= (n是正整数),即积的乘方,等于把积中的每一个因式分别进行乘方.
am+n
am-n
amn
anbn
2.乘法公式:
(1)平方差公式:(a+b)(a-b)= ,
(2)完全平方公式:(a±b)2= .
3.分解因式:
(1)分解因式是一种 变形,其形式为:一个多项式=几个
式 的形式.
(2)分解因式的具体方法: 分解因式; 分解因式.
a2-b2
a2±2ab+b2
恒等
整
积
提公因式法
运用公式法
专题一 幂的运算性质
1.下列计算正确的是 ( )
A.a3·a4=a12 B.a6÷a3=a2 C.(a3)2=a5 D.(-a2b)3=-a6b3
D
2.计算:42012·(-0.25)2013.
解:42012·(-0.25)2013
=42012·(-0.25)2012·(-0.25)
=(-1)2012·(-0.25)
=-0.25.
3.计算:2×3n+3n-3n+1.
解:方法一:
原式=3×3n-3n+1
=3n+1-3n+1
=0.
方法二:
原式=3×3n-3×3n
=0.
专题二 整式的乘除运算
4.计算:(2x2-5y3)·(-3x2y3).
解:(2x2-5y3)·(-3x2y3)
=(2x2)·(-3x2y3)+(-5y3)·(-3x2y3)
=-6x4y3+15x2y6.
5.先化简,再求值:x(x+2)-(x+1)(x-1),其中x=- .
解:因为x(x+2)-(x+1)(x-1)=x2+2x-(x2-x+x-1)=2x+1.
所以当x=- 时,原式=2×(- )+1=0.
【方法归纳交流】整式乘法运算时,一定要注意正确地确定积中每项的 ,并且必要时要利用整式的加减法则,将结果写成最简形式,即不含括号.
6.先化简,再求值:[(a-3b)(a+3b)+(3b-a)2]÷(2a),其中a=-3,b=10.
解:[(a-3b)(a+3b)+(3b-a)2]÷(2a)
=[a2-(3b)2+(3b)2-2·3b·a+a2]÷(2a)
=(2a2-6ba)÷(2a)=a-3b.
当a=-3,b=10时,原式=-3-3×10=-33.
符号
专题三 乘法公式的运用
8.用简便方法计算:(1)103×97-992;(2)(2+1)(22+1)(24+1)(28+1).
7.计算:(1)(-5x-y)2;(2)(-m-2n)(2n-m).
解:(1)原式=(-5x)2-2×(-5x)×y+(-y)2
=25x2+10xy+y2.
(2)原式=(-m-2n)(-m+2n)
=(-m)2-(2n)2
=m2-4n2.
解:(1)原式=(100+3)(100-3)-(100-1)2
=1002-9-(1002-200+1)
=1002-9-1002+200-1
=190.
(2)原式=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1.
解:(1)原式=(100+3)(100-3)-(100-1)2
=1002-9-(1002-200+1)
=1002-9-1002+200-1
=190.
9.计算:(1)化简(2a+3b-4c+5)(2a-3b+4c+5);
(2)(a- )2(a+ )2(a2+ )2.
[变式训练]已知a+b=3,ab=1,求(1)a2+b2;(2)(a-b)2;(3)a4+b4.
解:(1)因为(a+b)2=a2+2ab+b2,
所以有a2+b2=(a+b)2-2ab=32-2×1=7;
(2)因为(a-b)2=a2-2ab+b2,
结合(1)有(a-b)2=(a+b)2-4ab=32-4×1=5;
(3)a4+b4=(a2+b2)2-2a2b2=72-2×12=47.
(2)原式=[(a- )(a+ )]2 (a2+ )2
=[(a2- )(a2+ )]2=(a4- )2
=a8- a4+ .
专题四 幂和乘法公式的逆运算
10.计算:82010·(-0.125)2011.
解:82010·(-0.125)2011=82010·(-0.125)2010·(-0.125)
=[8·(-0.125)]2010·(-0.125)
=(-1)2010·(-0.125)
=-0.125.
[变式训练]已知5m=7,5m+3n=875,求2012n.
解:因为5m=7,
所以5m+3n=5m×53n=7×(53)n=7×125n,
因为5m+3n=875,
所以7×125n=875,125n=125,n=1,即2012n=2012.
专题五 整式运算中的思想方法
11.化简:12(2x-y)+7(y-2x)+9(2x-y)+5.
解:原式=12(2x-y)-7(2x-y)+9(2x-y)+5
=14(2x-y)+5
=28x-14y+5.
[变式训练]已知x2-xy=7,xy-y2=3,求代数式x2-y2与x2-2xy+y2的值.
解:因为x2-xy=7,xy-y2=3,
所以x2-xy+xy-y2=7+3,(x2-xy)-(xy-y2)=7-3,
所以x2-y2=10,x2-2xy+y2=4.
专题六 分解因式
12.分解因式:(1)a2-a;(2)x2+4x+4;(3)(x+2)(x+4)+x2-4.
解:(1)a2-a=a(a-1);
(2)x2+4x+4=(x+2)2;
(3)原式=x2+6x+8+x2-4
=2x2+6x+4=2(x2+3x+2)=2(x+1)(x+2).
13.计算:(a+3)(a-3)(a2+9).
解:(a+3)(a-3)(a2+9)
=(a2-9)(a2+9)
=a4-81
14.试求(2+1)(22+1)(24+1)…(232+1)+1的个位数字.
解:(2+1)(22+1)(24+1)…(232+1)+1
=(2-1)(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)…(232+1)+1
=…
=(264-1)+1=264=(24)16=1616
因此个位数字是6.
【方法归纳交流】解决这类题目时,先看式子的 特征,如果不具备公式的特点就需要进行构造.在同一题目中,可以连续多次使用 .
结构
公式
因式分解
复 习 课
1.能灵活运用幂的运算性质、整式乘除、乘法公式等知识解决问题.
2.知道提公因式法、运用公式法分解因式的方法,能选择合适的方法分解因式.
3.感受数学与现实生活的密切联系,学会用类比、转化的数学思想与方法.
4.重点:整式的概念,整式加减运算,幂的运算性质,整式乘除运算,乘法公式的综合运用.
体系构建
请你尝试补
充知识网络图.
am+n
am-n
amn
anbn
a2-b2
a2±2ab+b2
核心梳理
1.幂的运算性质:
(1)同底数幂的乘法性质:am·an= (m,n都是正整数),即同底数幂相乘,底数不变,指数相加.
(2)同底数幂的除法性质:am÷an= (a≠0,m,n都是正整数,且m>n),即同底数幂相除,底数不变,指数相减.
(3)幂的乘方的性质:(am)n= (m,n都是正整数),即幂的乘方,底数不变,指数相乘.
(4)积的乘方的性质:(ab)n= (n是正整数),即积的乘方,等于把积中的每一个因式分别进行乘方.
am+n
am-n
amn
anbn
2.乘法公式:
(1)平方差公式:(a+b)(a-b)= ,
(2)完全平方公式:(a±b)2= .
3.分解因式:
(1)分解因式是一种 变形,其形式为:一个多项式=几个
式 的形式.
(2)分解因式的具体方法: 分解因式; 分解因式.
a2-b2
a2±2ab+b2
恒等
整
积
提公因式法
运用公式法
专题一 幂的运算性质
1.下列计算正确的是 ( )
A.a3·a4=a12 B.a6÷a3=a2 C.(a3)2=a5 D.(-a2b)3=-a6b3
D
2.计算:42012·(-0.25)2013.
解:42012·(-0.25)2013
=42012·(-0.25)2012·(-0.25)
=(-1)2012·(-0.25)
=-0.25.
3.计算:2×3n+3n-3n+1.
解:方法一:
原式=3×3n-3n+1
=3n+1-3n+1
=0.
方法二:
原式=3×3n-3×3n
=0.
专题二 整式的乘除运算
4.计算:(2x2-5y3)·(-3x2y3).
解:(2x2-5y3)·(-3x2y3)
=(2x2)·(-3x2y3)+(-5y3)·(-3x2y3)
=-6x4y3+15x2y6.
5.先化简,再求值:x(x+2)-(x+1)(x-1),其中x=- .
解:因为x(x+2)-(x+1)(x-1)=x2+2x-(x2-x+x-1)=2x+1.
所以当x=- 时,原式=2×(- )+1=0.
【方法归纳交流】整式乘法运算时,一定要注意正确地确定积中每项的 ,并且必要时要利用整式的加减法则,将结果写成最简形式,即不含括号.
6.先化简,再求值:[(a-3b)(a+3b)+(3b-a)2]÷(2a),其中a=-3,b=10.
解:[(a-3b)(a+3b)+(3b-a)2]÷(2a)
=[a2-(3b)2+(3b)2-2·3b·a+a2]÷(2a)
=(2a2-6ba)÷(2a)=a-3b.
当a=-3,b=10时,原式=-3-3×10=-33.
符号
专题三 乘法公式的运用
8.用简便方法计算:(1)103×97-992;(2)(2+1)(22+1)(24+1)(28+1).
7.计算:(1)(-5x-y)2;(2)(-m-2n)(2n-m).
解:(1)原式=(-5x)2-2×(-5x)×y+(-y)2
=25x2+10xy+y2.
(2)原式=(-m-2n)(-m+2n)
=(-m)2-(2n)2
=m2-4n2.
解:(1)原式=(100+3)(100-3)-(100-1)2
=1002-9-(1002-200+1)
=1002-9-1002+200-1
=190.
(2)原式=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1.
解:(1)原式=(100+3)(100-3)-(100-1)2
=1002-9-(1002-200+1)
=1002-9-1002+200-1
=190.
9.计算:(1)化简(2a+3b-4c+5)(2a-3b+4c+5);
(2)(a- )2(a+ )2(a2+ )2.
[变式训练]已知a+b=3,ab=1,求(1)a2+b2;(2)(a-b)2;(3)a4+b4.
解:(1)因为(a+b)2=a2+2ab+b2,
所以有a2+b2=(a+b)2-2ab=32-2×1=7;
(2)因为(a-b)2=a2-2ab+b2,
结合(1)有(a-b)2=(a+b)2-4ab=32-4×1=5;
(3)a4+b4=(a2+b2)2-2a2b2=72-2×12=47.
(2)原式=[(a- )(a+ )]2 (a2+ )2
=[(a2- )(a2+ )]2=(a4- )2
=a8- a4+ .
专题四 幂和乘法公式的逆运算
10.计算:82010·(-0.125)2011.
解:82010·(-0.125)2011=82010·(-0.125)2010·(-0.125)
=[8·(-0.125)]2010·(-0.125)
=(-1)2010·(-0.125)
=-0.125.
[变式训练]已知5m=7,5m+3n=875,求2012n.
解:因为5m=7,
所以5m+3n=5m×53n=7×(53)n=7×125n,
因为5m+3n=875,
所以7×125n=875,125n=125,n=1,即2012n=2012.
专题五 整式运算中的思想方法
11.化简:12(2x-y)+7(y-2x)+9(2x-y)+5.
解:原式=12(2x-y)-7(2x-y)+9(2x-y)+5
=14(2x-y)+5
=28x-14y+5.
[变式训练]已知x2-xy=7,xy-y2=3,求代数式x2-y2与x2-2xy+y2的值.
解:因为x2-xy=7,xy-y2=3,
所以x2-xy+xy-y2=7+3,(x2-xy)-(xy-y2)=7-3,
所以x2-y2=10,x2-2xy+y2=4.
专题六 分解因式
12.分解因式:(1)a2-a;(2)x2+4x+4;(3)(x+2)(x+4)+x2-4.
解:(1)a2-a=a(a-1);
(2)x2+4x+4=(x+2)2;
(3)原式=x2+6x+8+x2-4
=2x2+6x+4=2(x2+3x+2)=2(x+1)(x+2).
13.计算:(a+3)(a-3)(a2+9).
解:(a+3)(a-3)(a2+9)
=(a2-9)(a2+9)
=a4-81
14.试求(2+1)(22+1)(24+1)…(232+1)+1的个位数字.
解:(2+1)(22+1)(24+1)…(232+1)+1
=(2-1)(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)…(232+1)+1
=…
=(264-1)+1=264=(24)16=1616
因此个位数字是6.
【方法归纳交流】解决这类题目时,先看式子的 特征,如果不具备公式的特点就需要进行构造.在同一题目中,可以连续多次使用 .
结构
公式
