第14章 统计章末复习提升课(共47张PPT)
文档属性
| 名称 | 第14章 统计章末复习提升课(共47张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-30 09:51:36 | ||
图片预览











文档简介
(共47张PPT)
第14章 统 计
章末复习提升课
01
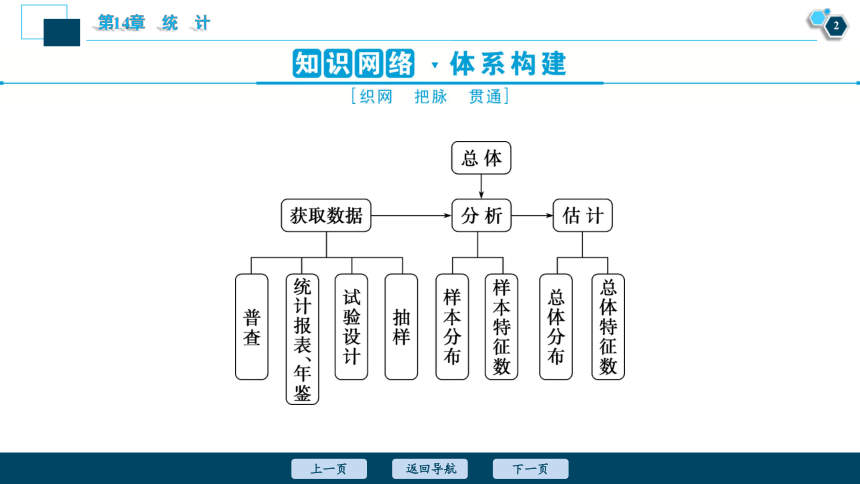
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
主题1 抽样方法
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量(单位:辆)如下表:
轿车A 轿车B 轿车C
舒适型 100 150 z
标准型 300 450 600
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中A类轿车有10辆.
(1)求z的值;
(2)用分层抽样的方法从C类轿车中抽取一个容量为5的样本,求舒适型、标准型的轿车应分别抽取多少辆?
应用抽样方法抽取样本应注意的问题
(1)用随机数表法抽样时,对个体所编的号码位数要相等.当问题所给位数不相等时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位 数.
(2)两种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数表法;当总体中个体差异较显著时,可采用分层抽样.
一个总体共有60个个体,其编号为00,01,02,…,59,现从中抽取一个容量为10的样本,请从随机数表的第8行第11列的数字开
始,向右读,到最后一列后再从下一行左边开始继续向右读,依次获取样本号码,直到取满样本为止,则获得的样本号码是______________.
附表:(第8行~第10行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79(第8行)
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54(第9行)
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62
90 52 84 77 27 08 02 73 43 28(第10行)
解析:第8行第11列的数字为1,由此开始,依次抽取号码,第一个号码为16,可取出;第二个号码为95>59,舍去.按照这个规则抽取号码,抽取的10个样本号码为16,55,19,10,50,12,58,07,44,39.
答案:16,55,19,10,50,12,58,07,44,39
主题2 统计图表
(多选)某报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图①,并将人均月收入绘制成如图②的不完整的条形统计图.
根据以上统计图,以下说法正确的是( )
A.2020年农民工人均月收入的增长率是10%
B.2018年农民工人均月收入是2 205元
C.小明认为“农民工2019年的人均月收入比2018年的少了”
D.2016年到2020年这五年中,2020年农民工人均月收入最高
√
√
√
【解析】 由折线统计图,知2020年农民工人均月收入的增长率是10%,则A说法正确.
由条形统计图,知2018年农民工人均月收入是2 205元,则B说法正确.
由题图,知2019年农民工人均月收入为2 205(1+20%)=2 646>2 205,故C说法错误.
由条形统计图,知2016年到2020年这五年中,2020年农民工人均月收入最高,则D说法正确.故选ABD.
此类问题主要考查统计图表的识别和应用,要会从图中读出相应的信 息,然后利用信息解决问题即可得结果.
某地区经过一年的新农村建设,农村的经济收入增加了一
倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
√
解析:设新农村建设前经济收入的总量为x,则新农村建设后经济收入的总量为2x.
建设前种植收入为0.6x,建设后种植收入为0.74x,故A不正确;
建设前其他收入为0.04x,建设后其他收入为0.1x,故B正确;
建设前养殖收入为0.3x,建设后养殖收入为0.6x,故C正确;
建设后养殖收入与第三产业收入的总和占建设后经济收入总量的58%,故D正确.故选A.
主题3 用样本估计总体的集中趋势参数
下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
【解】 (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
(2)画出频率直方图,如图所示.
与频率直方图有关问题的常见类型及解题策略
(1)已知频率直方图中的部分数据,求其他数据,可根据频率直方图中的数据求出样本与整体的关系,利用频率和等于1就可求出其他数据.
(2)已知频率直方图,求某种范围内的数据,可利用图形及某范围结合求解.
对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布表和频率直方图,如图所示:
分组 频数 频率
[10,15) 10 0.25
[15,20) 24 n
[20,25) m p
[25,30] 2 0.05
合计 M 1.00
(1)求表中M,p及图中a的值;
(2)若该校高三年级学生有240人,试估计该校高三年级学生参加社区服务的次数在区间[10,15)内的人数.
(2)因为该校高三年级学生有240人,分组[10,15)的频率是0.25,所以估计该校高三年级学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.
主题4 用样本估计总体的离散程度参数
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标
值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
(1)根据上表画出产品质量指标的频率直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
【解】 (1)产品质量指标的频率直方图如图.
(2)质量指标值的样本平均数为80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为s2=(-20)2×0.06+(-10)2×0.26+02×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定.
用样本估计总体的离散程度参数应注意的问题
(1)众数、中位数、平均数的含义及求法.
(2)方差、标准差的计算.
(3)中位数用来描述样本数据的中心位置,众数体现了数据的最大集中
点,平均数反映样本数据的总体水平.
(4)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差
(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
某单位开展“党员在线学习”活动,统计党员某周周一至周日(共7天)学习得分情况,下表是党员甲和党员乙学习得分情况:
党员甲学习得分情况
党员乙学习得分情况
日期 周一 周二 周三 周四 周五 周六 周日
得分 10 25 30 13 35 31 25
日期 周一 周二 周三 周四 周五 周六 周日
得分 35 26 15 20 25 17 30
(1)求本周党员乙周一至周日(共7天)学习得分的平均数和方差;
(2)根据本周某一天的数据,将全单位80名党员的学习得分按照[10,15),[15,20), [20,25),[25,30),[30,35]进行分组、绘制成频率直方图.
(如图)
已知这一天甲和乙学习得分在80名党员中排名分别为第30和第68名,请确定这是根据哪一天的数据制作的频率直方图.(直接写结果,不需要过程)
(2)周三.
由直方图知,学习得分落在[30,35],[25,30),[20,25),[15,20),
[10,15)区间内的人数依次为:80×0.15=12人,80×0.25=20人,80×0.3=24人,80×0.2=16人,80×0.1=8人,
由甲学习得分排名第30,可知当天甲学习得分在[25,30),只有周二、周三和周日;
由乙学习得分排名第68,可知当天乙学习得分在[15,20),只有周三和周六;
所以周三符合要求.
1.某学校高一、高二年级共有1 800人,现按照分层抽样的方法,抽取90人作为样本进行某项调查.若样本中高一年级学生有42人,则该校高一年级学生共有( )
A.420人 B.480人
C.840人 D.960人
√
2.一支田径队有男运动员 560 人,女运动员 420 人,为了了解运动员的健康情况,从男运动员中任意抽取 16 人,从女生中任意抽取 12 人进行调查,这种抽样方法是( )
A.简单随机抽样法 B.抽签法
C.随机数表法 D.分层抽样法
解析:总体由男生和女生组成,比例为560∶420=4∶3,所抽取的比例也是16∶12=4∶3.符合分层抽样,故选D.
√
3.如图所示是一容量为100的样本的频率直方图,则由图形中的数据,样本落在[5,10)内的频数为( )
A.50
B.40
C.30
D.20
解析:第一个小矩形的面积为0.04×5=0.2, 所以样本落在[5,10)内的频数为0.2×100=20.故选D.
√
4.空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI
指数值 0~50 51~100 101~150 151~200 201~300 >300
空气
质量 优 良 轻度
污染 中度
污染 重度
污染 严重
污染
如图是某市10月1日-20日AQI指数变化趋势:
√
解析:对A,因为第10天与第11天AQI指数值都略高100,所以中位数高于100,正确;
对C,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对D,由图知,10月上旬大部分AQI指数在100以下,10月中旬大部分AQI指数在100以上,所以正确,故选C.
请做:章末演练 轻松闯关
word部分:
点击进入链接
本部分内容讲解结束
第14章 统 计
章末复习提升课
01
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
主题1 抽样方法
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量(单位:辆)如下表:
轿车A 轿车B 轿车C
舒适型 100 150 z
标准型 300 450 600
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中A类轿车有10辆.
(1)求z的值;
(2)用分层抽样的方法从C类轿车中抽取一个容量为5的样本,求舒适型、标准型的轿车应分别抽取多少辆?
应用抽样方法抽取样本应注意的问题
(1)用随机数表法抽样时,对个体所编的号码位数要相等.当问题所给位数不相等时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位 数.
(2)两种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数表法;当总体中个体差异较显著时,可采用分层抽样.
一个总体共有60个个体,其编号为00,01,02,…,59,现从中抽取一个容量为10的样本,请从随机数表的第8行第11列的数字开
始,向右读,到最后一列后再从下一行左边开始继续向右读,依次获取样本号码,直到取满样本为止,则获得的样本号码是______________.
附表:(第8行~第10行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79(第8行)
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54(第9行)
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62
90 52 84 77 27 08 02 73 43 28(第10行)
解析:第8行第11列的数字为1,由此开始,依次抽取号码,第一个号码为16,可取出;第二个号码为95>59,舍去.按照这个规则抽取号码,抽取的10个样本号码为16,55,19,10,50,12,58,07,44,39.
答案:16,55,19,10,50,12,58,07,44,39
主题2 统计图表
(多选)某报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图①,并将人均月收入绘制成如图②的不完整的条形统计图.
根据以上统计图,以下说法正确的是( )
A.2020年农民工人均月收入的增长率是10%
B.2018年农民工人均月收入是2 205元
C.小明认为“农民工2019年的人均月收入比2018年的少了”
D.2016年到2020年这五年中,2020年农民工人均月收入最高
√
√
√
【解析】 由折线统计图,知2020年农民工人均月收入的增长率是10%,则A说法正确.
由条形统计图,知2018年农民工人均月收入是2 205元,则B说法正确.
由题图,知2019年农民工人均月收入为2 205(1+20%)=2 646>2 205,故C说法错误.
由条形统计图,知2016年到2020年这五年中,2020年农民工人均月收入最高,则D说法正确.故选ABD.
此类问题主要考查统计图表的识别和应用,要会从图中读出相应的信 息,然后利用信息解决问题即可得结果.
某地区经过一年的新农村建设,农村的经济收入增加了一
倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
√
解析:设新农村建设前经济收入的总量为x,则新农村建设后经济收入的总量为2x.
建设前种植收入为0.6x,建设后种植收入为0.74x,故A不正确;
建设前其他收入为0.04x,建设后其他收入为0.1x,故B正确;
建设前养殖收入为0.3x,建设后养殖收入为0.6x,故C正确;
建设后养殖收入与第三产业收入的总和占建设后经济收入总量的58%,故D正确.故选A.
主题3 用样本估计总体的集中趋势参数
下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
【解】 (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
(2)画出频率直方图,如图所示.
与频率直方图有关问题的常见类型及解题策略
(1)已知频率直方图中的部分数据,求其他数据,可根据频率直方图中的数据求出样本与整体的关系,利用频率和等于1就可求出其他数据.
(2)已知频率直方图,求某种范围内的数据,可利用图形及某范围结合求解.
对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布表和频率直方图,如图所示:
分组 频数 频率
[10,15) 10 0.25
[15,20) 24 n
[20,25) m p
[25,30] 2 0.05
合计 M 1.00
(1)求表中M,p及图中a的值;
(2)若该校高三年级学生有240人,试估计该校高三年级学生参加社区服务的次数在区间[10,15)内的人数.
(2)因为该校高三年级学生有240人,分组[10,15)的频率是0.25,所以估计该校高三年级学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.
主题4 用样本估计总体的离散程度参数
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标
值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
(1)根据上表画出产品质量指标的频率直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
【解】 (1)产品质量指标的频率直方图如图.
(2)质量指标值的样本平均数为80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为s2=(-20)2×0.06+(-10)2×0.26+02×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定.
用样本估计总体的离散程度参数应注意的问题
(1)众数、中位数、平均数的含义及求法.
(2)方差、标准差的计算.
(3)中位数用来描述样本数据的中心位置,众数体现了数据的最大集中
点,平均数反映样本数据的总体水平.
(4)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差
(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
某单位开展“党员在线学习”活动,统计党员某周周一至周日(共7天)学习得分情况,下表是党员甲和党员乙学习得分情况:
党员甲学习得分情况
党员乙学习得分情况
日期 周一 周二 周三 周四 周五 周六 周日
得分 10 25 30 13 35 31 25
日期 周一 周二 周三 周四 周五 周六 周日
得分 35 26 15 20 25 17 30
(1)求本周党员乙周一至周日(共7天)学习得分的平均数和方差;
(2)根据本周某一天的数据,将全单位80名党员的学习得分按照[10,15),[15,20), [20,25),[25,30),[30,35]进行分组、绘制成频率直方图.
(如图)
已知这一天甲和乙学习得分在80名党员中排名分别为第30和第68名,请确定这是根据哪一天的数据制作的频率直方图.(直接写结果,不需要过程)
(2)周三.
由直方图知,学习得分落在[30,35],[25,30),[20,25),[15,20),
[10,15)区间内的人数依次为:80×0.15=12人,80×0.25=20人,80×0.3=24人,80×0.2=16人,80×0.1=8人,
由甲学习得分排名第30,可知当天甲学习得分在[25,30),只有周二、周三和周日;
由乙学习得分排名第68,可知当天乙学习得分在[15,20),只有周三和周六;
所以周三符合要求.
1.某学校高一、高二年级共有1 800人,现按照分层抽样的方法,抽取90人作为样本进行某项调查.若样本中高一年级学生有42人,则该校高一年级学生共有( )
A.420人 B.480人
C.840人 D.960人
√
2.一支田径队有男运动员 560 人,女运动员 420 人,为了了解运动员的健康情况,从男运动员中任意抽取 16 人,从女生中任意抽取 12 人进行调查,这种抽样方法是( )
A.简单随机抽样法 B.抽签法
C.随机数表法 D.分层抽样法
解析:总体由男生和女生组成,比例为560∶420=4∶3,所抽取的比例也是16∶12=4∶3.符合分层抽样,故选D.
√
3.如图所示是一容量为100的样本的频率直方图,则由图形中的数据,样本落在[5,10)内的频数为( )
A.50
B.40
C.30
D.20
解析:第一个小矩形的面积为0.04×5=0.2, 所以样本落在[5,10)内的频数为0.2×100=20.故选D.
√
4.空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI
指数值 0~50 51~100 101~150 151~200 201~300 >300
空气
质量 优 良 轻度
污染 中度
污染 重度
污染 严重
污染
如图是某市10月1日-20日AQI指数变化趋势:
√
解析:对A,因为第10天与第11天AQI指数值都略高100,所以中位数高于100,正确;
对C,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对D,由图知,10月上旬大部分AQI指数在100以下,10月中旬大部分AQI指数在100以上,所以正确,故选C.
请做:章末演练 轻松闯关
word部分:
点击进入链接
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
