2021-2022学年鲁教版(五四制)八年级下册数学 7.4 二次根式的乘除 教案(表格式)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级下册数学 7.4 二次根式的乘除 教案(表格式) | 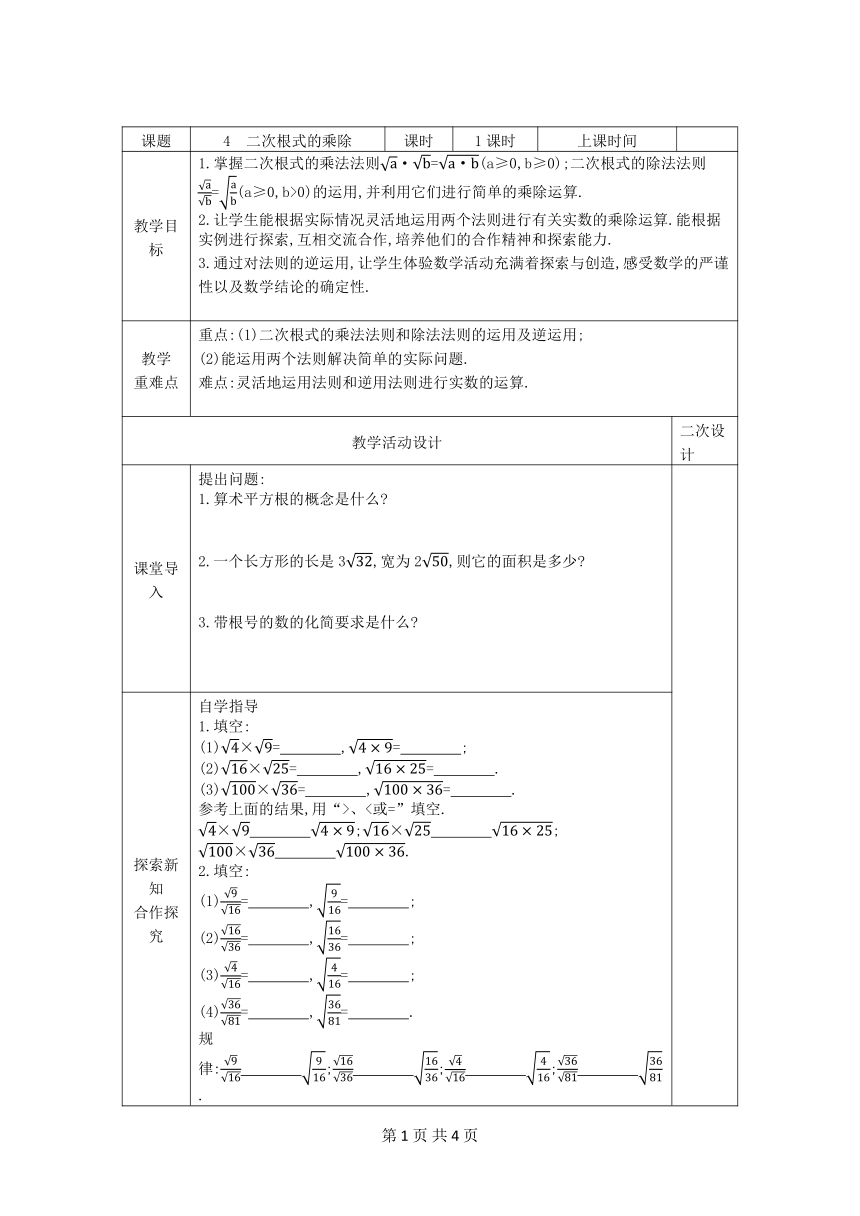 | |
| 格式 | docx | ||
| 文件大小 | 61.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-30 10:51:16 | ||
图片预览


文档简介
课题 4 二次根式的乘除 课时 1课时 上课时间
教学目标 1.掌握二次根式的乘法法则·=(a≥0,b≥0);二次根式的除法法则=(a≥0,b>0)的运用,并利用它们进行简单的乘除运算. 2.让学生能根据实际情况灵活地运用两个法则进行有关实数的乘除运算.能根据实例进行探索,互相交流合作,培养他们的合作精神和探索能力. 3.通过对法则的逆运用,让学生体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性.
教学 重难点 重点:(1)二次根式的乘法法则和除法法则的运用及逆运用; (2)能运用两个法则解决简单的实际问题. 难点:灵活地运用法则和逆用法则进行实数的运算.
教学活动设计 二次设计
课堂导入 提出问题: 1.算术平方根的概念是什么 2.一个长方形的长是3,宽为2,则它的面积是多少 3.带根号的数的化简要求是什么
探索新知 合作探究 自学指导 1.填空: (1)×= ,= ; (2)×= ,= . (3)×= ,= . 参考上面的结果,用“>、<或=”填空. × ;× ; × . 2.填空: (1)= ,= ; (2)= ,= ; (3)= ,= ; (4)= ,= . 规律: ; ; ; .
续表
探索新知 合作探究 3.认真阅读课本42~45页的内容,思考解决下列问题: (1)下面正方形的边长分别是多少 (2)这两个数之间有什么关系 (3)你能借助什么运算法则或运算律解释它吗 合作探究 通过计算总结运算法则: 1.二次根式的乘法法则:·=(a≥0,b≥0), 反之=·(a≥0,b≥0). 2.二次根式的除法法则:=(a≥0,b>0), 反之=(a≥0,b>0). [例1] 计算: (1)×; (2)×; (3)×; (4)×; (5)3×2. [例2] 化简: (1); (2); (3); (4); (5). [例3] 计算: (1); (2)÷; (3)÷; (4); (5)2÷4. [例4] 化简: (1); (2); (3); (4). [例5] 计算: (1)·(+5); (2)(2-2)(3+); (3)(2-)2.
续表
探索新知 合作探究 教师指导 1.易错点: (1)在进行二次根式的乘除运算时要注意隐含条件“中的a≥0”. (2)运算时注意符号与法则. 2.归纳小结: 二次根式的乘除运算步骤 (1)二次根式的乘法运算:二次根式相乘,把被开方数相乘;二次根式前面有系数时,把系数及被开方数分别相乘; (2)二次根式的除法运算:二次根式相除,把被开方数相除;二次根式前面有系数时,把系数及被开方数分别相除; (3)各项中有理数和无理数可以分开运算; (4)合理运用乘除法相关法则; (3)如果是单项式乘以多项式或者多项式之间相乘,可以运用相关的法则. 3.方法规律: ·=(a≥0,b≥0),=(a≥0,b>0).
当堂训练 1.计算÷÷的结果是( ) (A) (B) (C) (D) 2.计算: (1)×; (2); (3)×; (4)2÷4; (5)-2÷3×6.
板书设计
二次根式的乘除 1.·=(a≥0,b≥0) 2.=(a≥0,b>0)
教学反思
本节课由问题情境带领学生去复习有关知识,经历观察、对比、归纳、总结以及由具体到抽象、由特殊到一般的学习过程,让学生体会到研究问题解决问题的方法,从而加深对所学知识的理解,以此增强学生学好数学的愿望和信心.
(
第
1
页 共
1
页
)
教学目标 1.掌握二次根式的乘法法则·=(a≥0,b≥0);二次根式的除法法则=(a≥0,b>0)的运用,并利用它们进行简单的乘除运算. 2.让学生能根据实际情况灵活地运用两个法则进行有关实数的乘除运算.能根据实例进行探索,互相交流合作,培养他们的合作精神和探索能力. 3.通过对法则的逆运用,让学生体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性.
教学 重难点 重点:(1)二次根式的乘法法则和除法法则的运用及逆运用; (2)能运用两个法则解决简单的实际问题. 难点:灵活地运用法则和逆用法则进行实数的运算.
教学活动设计 二次设计
课堂导入 提出问题: 1.算术平方根的概念是什么 2.一个长方形的长是3,宽为2,则它的面积是多少 3.带根号的数的化简要求是什么
探索新知 合作探究 自学指导 1.填空: (1)×= ,= ; (2)×= ,= . (3)×= ,= . 参考上面的结果,用“>、<或=”填空. × ;× ; × . 2.填空: (1)= ,= ; (2)= ,= ; (3)= ,= ; (4)= ,= . 规律: ; ; ; .
续表
探索新知 合作探究 3.认真阅读课本42~45页的内容,思考解决下列问题: (1)下面正方形的边长分别是多少 (2)这两个数之间有什么关系 (3)你能借助什么运算法则或运算律解释它吗 合作探究 通过计算总结运算法则: 1.二次根式的乘法法则:·=(a≥0,b≥0), 反之=·(a≥0,b≥0). 2.二次根式的除法法则:=(a≥0,b>0), 反之=(a≥0,b>0). [例1] 计算: (1)×; (2)×; (3)×; (4)×; (5)3×2. [例2] 化简: (1); (2); (3); (4); (5). [例3] 计算: (1); (2)÷; (3)÷; (4); (5)2÷4. [例4] 化简: (1); (2); (3); (4). [例5] 计算: (1)·(+5); (2)(2-2)(3+); (3)(2-)2.
续表
探索新知 合作探究 教师指导 1.易错点: (1)在进行二次根式的乘除运算时要注意隐含条件“中的a≥0”. (2)运算时注意符号与法则. 2.归纳小结: 二次根式的乘除运算步骤 (1)二次根式的乘法运算:二次根式相乘,把被开方数相乘;二次根式前面有系数时,把系数及被开方数分别相乘; (2)二次根式的除法运算:二次根式相除,把被开方数相除;二次根式前面有系数时,把系数及被开方数分别相除; (3)各项中有理数和无理数可以分开运算; (4)合理运用乘除法相关法则; (3)如果是单项式乘以多项式或者多项式之间相乘,可以运用相关的法则. 3.方法规律: ·=(a≥0,b≥0),=(a≥0,b>0).
当堂训练 1.计算÷÷的结果是( ) (A) (B) (C) (D) 2.计算: (1)×; (2); (3)×; (4)2÷4; (5)-2÷3×6.
板书设计
二次根式的乘除 1.·=(a≥0,b≥0) 2.=(a≥0,b>0)
教学反思
本节课由问题情境带领学生去复习有关知识,经历观察、对比、归纳、总结以及由具体到抽象、由特殊到一般的学习过程,让学生体会到研究问题解决问题的方法,从而加深对所学知识的理解,以此增强学生学好数学的愿望和信心.
(
第
1
页 共
1
页
)
