五年级上册数学课件-第5节 探索活动:梯形的面积北师大版 (共25张PPT)
文档属性
| 名称 | 五年级上册数学课件-第5节 探索活动:梯形的面积北师大版 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-30 16:55:21 | ||
图片预览






文档简介
(共25张PPT)
第4单元 多边形的面积
第5节 探索活动:梯形的面积
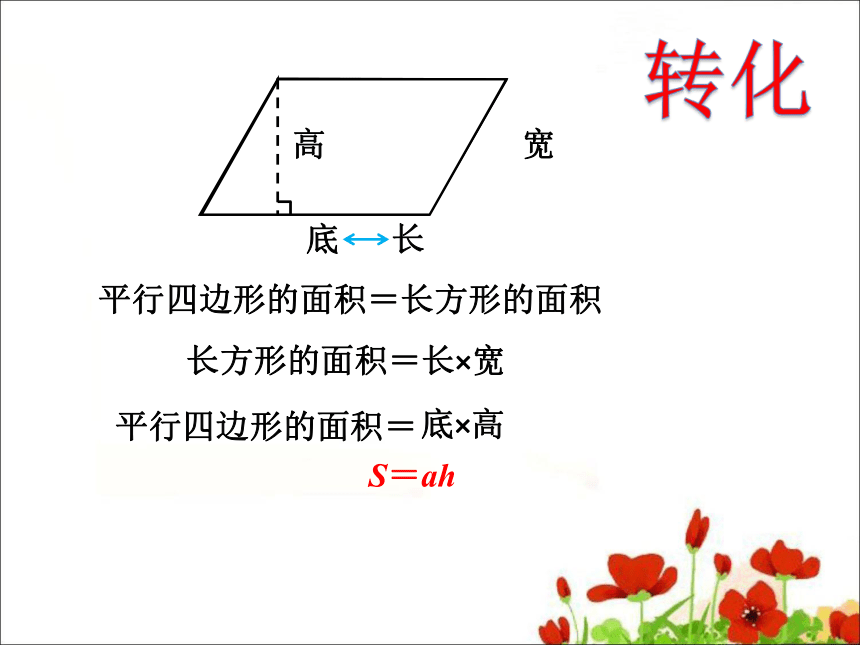
以旧引新
高
底
长
宽
平行四边形的面积=长方形的面积
长方形的面积=长×宽
底×高
平行四边形的面积=
S=ah
转化
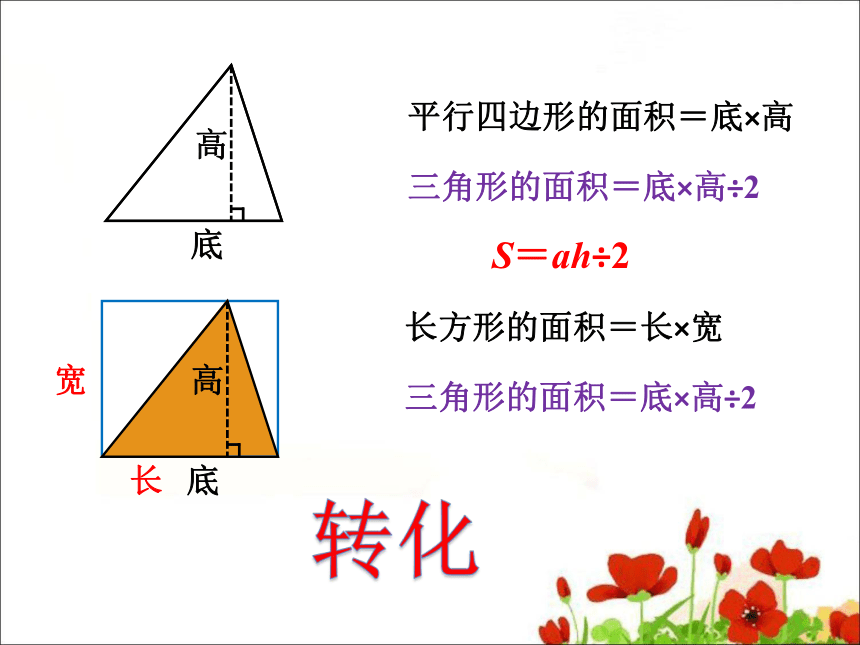
底
高
底
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
长方形的面积=长×宽
三角形的面积=底×高÷2
长
宽
S=ah÷2
转化
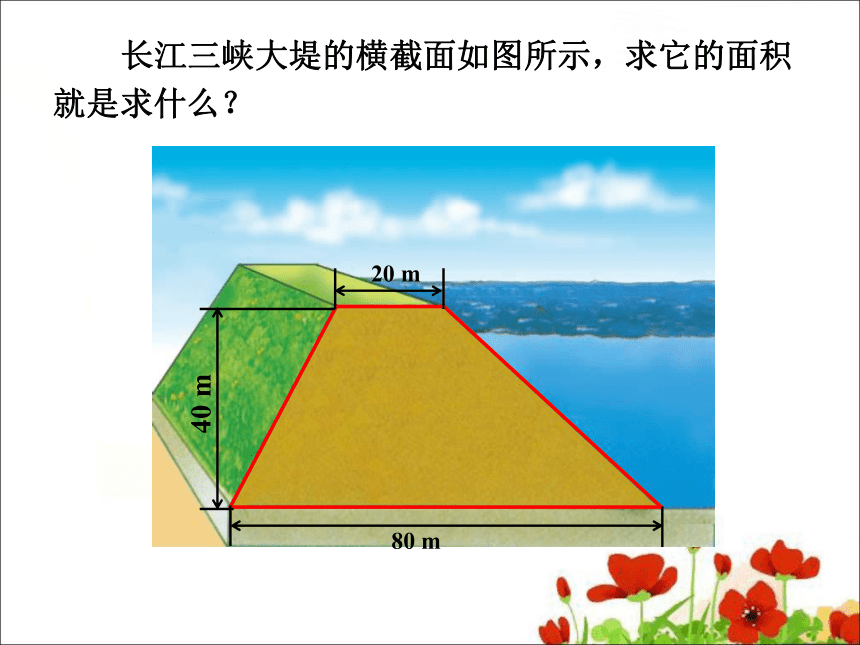
设置情境,提出问题
长江三峡大堤的横截面如图所示,求它的面积就是求什么?
20 m
80 m
40 m
在我们的生活中有很多这样的梯形需要我们计算它们的面积,但是梯形面积怎样计算呢?梯形的面积可能与什么有关?你想怎样推导出梯形面积的计算公式呢?
转化
提供材料,合作探究
小组合作:
(1)先独立思考能把梯形转化成已学过的什么图形,再按照“转化—找联系—推导公式”的思路来研究;
(2)小组交流后共同验证。
把梯形转化成学过的图形。
上底
下底
上底
下底
高
平行四边形的面积
=底×高
=(上底+下底)×高
梯形的面积
=(上底+下底)×高÷2
S=(a+b)×h÷2
方法一:
上底
下底
上底
下底
高
长方形的面积
=底×高
梯形的面积
=长方形的面积÷2
=(上底+下底)×高÷2
S=(a+b)×h÷2
方法二:
形状相同、大小相等的直角梯形且上底与下底的和正好与梯形的高相等,这样的两个梯形可以拼成一个正方形。
想一想:两个怎样的梯形可以拼成正方形呢?
小结:两个完全一样的梯形就能拼成一个平行四边形或长方形或正方形。
方法三:
上底
下底
高
高
a的面积=上底×高÷2
梯形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
S=(a+b)×h÷2
a
b
b的面积=下底×高÷2
下底
上底
高÷2
平行四边形的面积
=底×高
=(上底+下底)×(高÷2)
梯形的面积
=(上底+下底)×高÷2
方法四:
S=(a+b)×h÷2
归纳总结,提高认识
上述的方法虽然操作过程不同,但是它们之间却有着共同点,谁来说一说共同点是什么呢?
转化
梯形的面积=(上底+下底)×高÷2
S=(a+b)×h÷2
实践运用,解决问题
(20+80)×40÷2=2000(m2)
20 m
80 m
40 m
篮球场的罚球区面积是多少?
(3.6+6.5)×5.8÷2=29.29(平方米)
5.8米
6.5米
3.6米
学校靠墙的一个花坛,周围篱笆的长度是46 m,你能算出它的面积吗?
20米
46-20=26(米)
上底+下底:
26×20÷2=260(平方米)
花园面积:
反思收获,拓展延伸
这节课同学们在探索的过程中发挥了自己的聪明才智,创造出了多种推导梯形面积计算公式的方法,而且能够用所学知识解决生活中的问题,相信同学们一定有许多收获。你还有什么疑问吗?
课后作业
完成教材第60页练一练第1~5题。
第4单元 多边形的面积
第5节 探索活动:梯形的面积
以旧引新
高
底
长
宽
平行四边形的面积=长方形的面积
长方形的面积=长×宽
底×高
平行四边形的面积=
S=ah
转化
底
高
底
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
长方形的面积=长×宽
三角形的面积=底×高÷2
长
宽
S=ah÷2
转化
设置情境,提出问题
长江三峡大堤的横截面如图所示,求它的面积就是求什么?
20 m
80 m
40 m
在我们的生活中有很多这样的梯形需要我们计算它们的面积,但是梯形面积怎样计算呢?梯形的面积可能与什么有关?你想怎样推导出梯形面积的计算公式呢?
转化
提供材料,合作探究
小组合作:
(1)先独立思考能把梯形转化成已学过的什么图形,再按照“转化—找联系—推导公式”的思路来研究;
(2)小组交流后共同验证。
把梯形转化成学过的图形。
上底
下底
上底
下底
高
平行四边形的面积
=底×高
=(上底+下底)×高
梯形的面积
=(上底+下底)×高÷2
S=(a+b)×h÷2
方法一:
上底
下底
上底
下底
高
长方形的面积
=底×高
梯形的面积
=长方形的面积÷2
=(上底+下底)×高÷2
S=(a+b)×h÷2
方法二:
形状相同、大小相等的直角梯形且上底与下底的和正好与梯形的高相等,这样的两个梯形可以拼成一个正方形。
想一想:两个怎样的梯形可以拼成正方形呢?
小结:两个完全一样的梯形就能拼成一个平行四边形或长方形或正方形。
方法三:
上底
下底
高
高
a的面积=上底×高÷2
梯形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
S=(a+b)×h÷2
a
b
b的面积=下底×高÷2
下底
上底
高÷2
平行四边形的面积
=底×高
=(上底+下底)×(高÷2)
梯形的面积
=(上底+下底)×高÷2
方法四:
S=(a+b)×h÷2
归纳总结,提高认识
上述的方法虽然操作过程不同,但是它们之间却有着共同点,谁来说一说共同点是什么呢?
转化
梯形的面积=(上底+下底)×高÷2
S=(a+b)×h÷2
实践运用,解决问题
(20+80)×40÷2=2000(m2)
20 m
80 m
40 m
篮球场的罚球区面积是多少?
(3.6+6.5)×5.8÷2=29.29(平方米)
5.8米
6.5米
3.6米
学校靠墙的一个花坛,周围篱笆的长度是46 m,你能算出它的面积吗?
20米
46-20=26(米)
上底+下底:
26×20÷2=260(平方米)
花园面积:
反思收获,拓展延伸
这节课同学们在探索的过程中发挥了自己的聪明才智,创造出了多种推导梯形面积计算公式的方法,而且能够用所学知识解决生活中的问题,相信同学们一定有许多收获。你还有什么疑问吗?
课后作业
完成教材第60页练一练第1~5题。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
