新课标北师大版六上1.6《圆的面积(二)》课件(20张PPT)
文档属性
| 名称 | 新课标北师大版六上1.6《圆的面积(二)》课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 10:58:28 | ||
图片预览





文档简介
(共20张PPT)
圆的面积(二)
北师大版六年级上册
教学目标
1.学习目标描述:能正确运用圆的面积公式计算圆的面积, 并能运用圆面积知识解决一些简单实际的问题。
2.学习内容分析:本课是在学生学习了圆的周长、圆的面积计算公式及推导过程的基础上进行教学的。本课从一个喷水头转动可以浇灌多大面积的农田的实例出发,结合学生的生活经验引出圆的面积知识。学习本节课,不但可以加强学生对前面知识的进一步理解,同时
教学目标
让学生学会准确地应用圆的面积计算公式解决一些简单的实际问题。
3.学科核心素养分析:通过运用圆的面积公式解决简单实际的问题,感受数学与现实生活的密切联系,体会数学的应用价值,激发学生热爱数学的情感。
新知导入
1.算一算。
12=
22=
32=
42=
52=
62=
102=
112=
1
4
9
16
25
36
100
121
新知导入
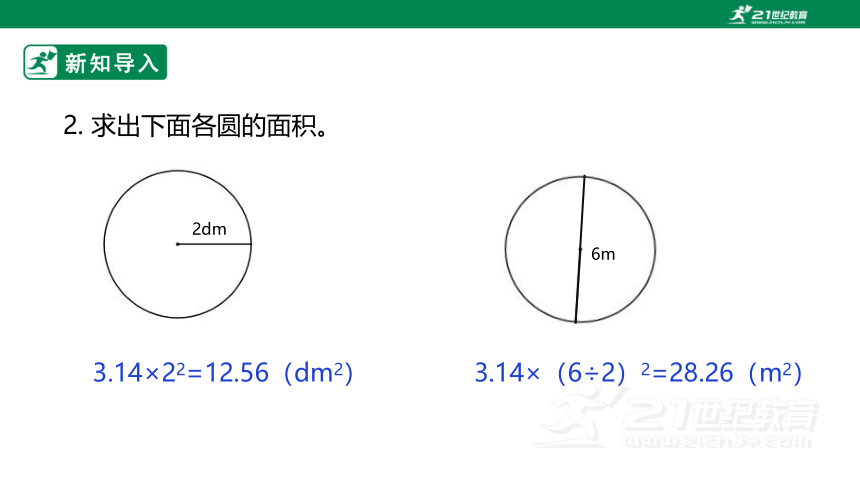
2. 求出下面各圆的面积。
2dm
3.14×22=12.56(dm2)
3.14×(6÷2)2=28.26(m2)
6m
新知导入
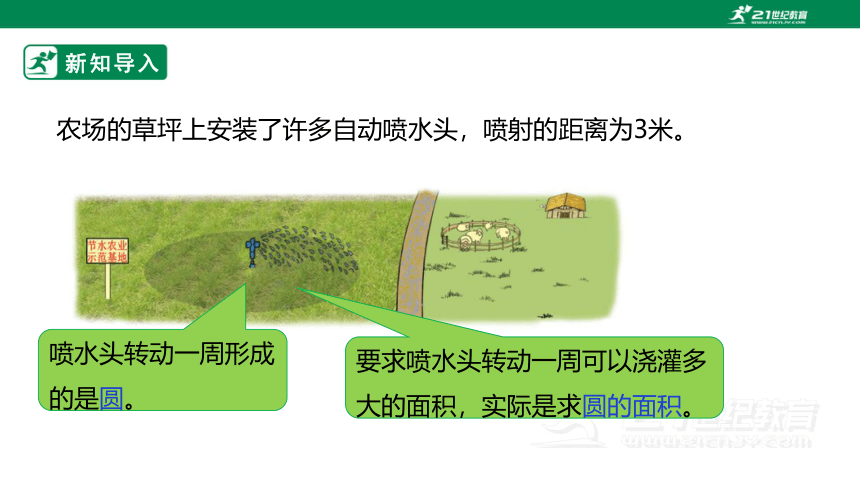
农场的草坪上安装了许多自动喷水头,喷射的距离为3米。
喷水头转动一周形成的是圆。
要求喷水头转动一周可以浇灌多大的面积,实际是求圆的面积。
新知讲解
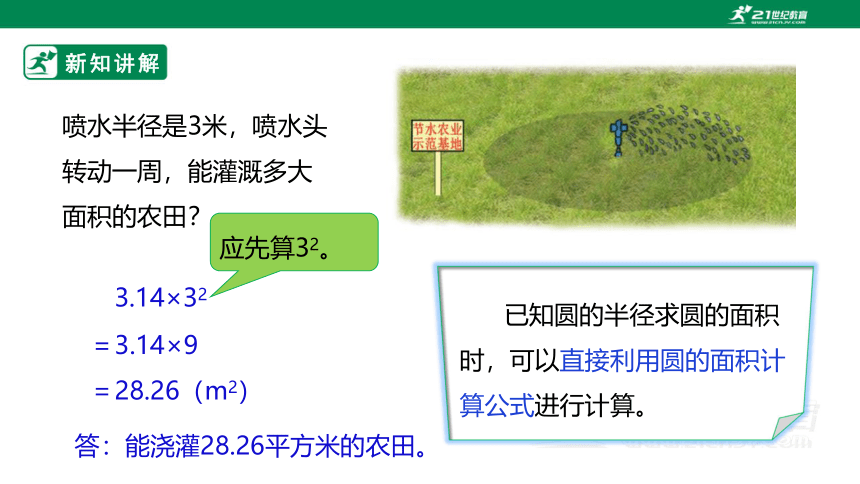
喷水半径是3米,喷水头转动一周,能灌溉多大面积的农田?
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
应先算32。
已知圆的半径求圆的面积时,可以直接利用圆的面积计算公式进行计算。
新知讲解
量的圆形羊圈的周长是125.6m,这个羊圈的面积是多少平方米?
羊圈的面积
先求出羊圈的半径
C=2πr
r=C÷π÷2
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
新知讲解
已知圆的周长求圆的面积,可以先求出圆的半径,然后直接利用圆的面积公式计算。
新知讲解
下面是一种有意思的推导圆面积的方法。
沿线剪开
这是一个由草绳编织成的圆形茶杯垫片。
像三角形,形状变了。
它们的面积一样,面积没变。
这时,三角形的面积相当于圆的面积。
观察这个三角形,底相当于圆的( ),高相当于圆的( )。
三角形的面积= ,所以圆的面积S= =( )。
底×高
2
( )×( )
2
新知讲解
这个三角形与原来的圆有什么关系呢?想一想,填一填。
周长
半径
2πr
r
πr2
课堂练习
1.求出下面各圆的面积。
(1)r=1厘米
(2)d=10米
(3)C=18.84分米
3.14×12=3.14(平方厘米)
3.14×(10÷2)2=78.5(平方米)
3.14×(18.84÷3.14÷2)2=28.26(平方分米)
课堂练习
2.在下面的长方形内画一个最大的圆,并求出圆的面积。
12厘米
8厘米
圆的直径等于正方形的宽。
3.14×(8÷2)2=50.24(平方厘米)
答:圆的面积是50.24平方厘米。
课堂练习
3.如图,直角梯形中,高是5厘米,下底是14厘米,求阴影部分的面积?
(5×2+14)×5÷2-3.14×52÷2
=24×5÷2-3.14×25÷2
=60-39.25
=20.75(平方厘米)
答:阴影部分的面积是20.75平方厘米。
阴影部分的面积等于梯形的面积减去半圆的面积。
课堂练习
4.拓展应用:圆形花坛周围有一条环形小路,花坛直径8米,小路宽2米,这条环形小路占地多少平方米?
8米
2米
阴影部分的面积等于大圆面积减小圆面积。
3.14×[(8÷2+2)2-(8÷2)2]
=3.14×20
=62.8(平方米)
答:这条环形小路的占地62.8平方米。
S环=π×(R2-r2)
课堂总结
通过今天的学习,你有哪些收获?
我会用圆的面积公式解决实际问题。
我还知道圆还能转化成三角形,真有趣!
板书设计
圆的面积(二)
——解决问题
已知半径:S=πr2
圆的面积
已知周长:先求半径
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
圆的面积(二)
北师大版六年级上册
教学目标
1.学习目标描述:能正确运用圆的面积公式计算圆的面积, 并能运用圆面积知识解决一些简单实际的问题。
2.学习内容分析:本课是在学生学习了圆的周长、圆的面积计算公式及推导过程的基础上进行教学的。本课从一个喷水头转动可以浇灌多大面积的农田的实例出发,结合学生的生活经验引出圆的面积知识。学习本节课,不但可以加强学生对前面知识的进一步理解,同时
教学目标
让学生学会准确地应用圆的面积计算公式解决一些简单的实际问题。
3.学科核心素养分析:通过运用圆的面积公式解决简单实际的问题,感受数学与现实生活的密切联系,体会数学的应用价值,激发学生热爱数学的情感。
新知导入
1.算一算。
12=
22=
32=
42=
52=
62=
102=
112=
1
4
9
16
25
36
100
121
新知导入
2. 求出下面各圆的面积。
2dm
3.14×22=12.56(dm2)
3.14×(6÷2)2=28.26(m2)
6m
新知导入
农场的草坪上安装了许多自动喷水头,喷射的距离为3米。
喷水头转动一周形成的是圆。
要求喷水头转动一周可以浇灌多大的面积,实际是求圆的面积。
新知讲解
喷水半径是3米,喷水头转动一周,能灌溉多大面积的农田?
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26平方米的农田。
应先算32。
已知圆的半径求圆的面积时,可以直接利用圆的面积计算公式进行计算。
新知讲解
量的圆形羊圈的周长是125.6m,这个羊圈的面积是多少平方米?
羊圈的面积
先求出羊圈的半径
C=2πr
r=C÷π÷2
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256平方米。
面积:3.14×202=1256(m2)
新知讲解
已知圆的周长求圆的面积,可以先求出圆的半径,然后直接利用圆的面积公式计算。
新知讲解
下面是一种有意思的推导圆面积的方法。
沿线剪开
这是一个由草绳编织成的圆形茶杯垫片。
像三角形,形状变了。
它们的面积一样,面积没变。
这时,三角形的面积相当于圆的面积。
观察这个三角形,底相当于圆的( ),高相当于圆的( )。
三角形的面积= ,所以圆的面积S= =( )。
底×高
2
( )×( )
2
新知讲解
这个三角形与原来的圆有什么关系呢?想一想,填一填。
周长
半径
2πr
r
πr2
课堂练习
1.求出下面各圆的面积。
(1)r=1厘米
(2)d=10米
(3)C=18.84分米
3.14×12=3.14(平方厘米)
3.14×(10÷2)2=78.5(平方米)
3.14×(18.84÷3.14÷2)2=28.26(平方分米)
课堂练习
2.在下面的长方形内画一个最大的圆,并求出圆的面积。
12厘米
8厘米
圆的直径等于正方形的宽。
3.14×(8÷2)2=50.24(平方厘米)
答:圆的面积是50.24平方厘米。
课堂练习
3.如图,直角梯形中,高是5厘米,下底是14厘米,求阴影部分的面积?
(5×2+14)×5÷2-3.14×52÷2
=24×5÷2-3.14×25÷2
=60-39.25
=20.75(平方厘米)
答:阴影部分的面积是20.75平方厘米。
阴影部分的面积等于梯形的面积减去半圆的面积。
课堂练习
4.拓展应用:圆形花坛周围有一条环形小路,花坛直径8米,小路宽2米,这条环形小路占地多少平方米?
8米
2米
阴影部分的面积等于大圆面积减小圆面积。
3.14×[(8÷2+2)2-(8÷2)2]
=3.14×20
=62.8(平方米)
答:这条环形小路的占地62.8平方米。
S环=π×(R2-r2)
课堂总结
通过今天的学习,你有哪些收获?
我会用圆的面积公式解决实际问题。
我还知道圆还能转化成三角形,真有趣!
板书设计
圆的面积(二)
——解决问题
已知半径:S=πr2
圆的面积
已知周长:先求半径
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
