第6章实数复习课件
图片预览








文档简介
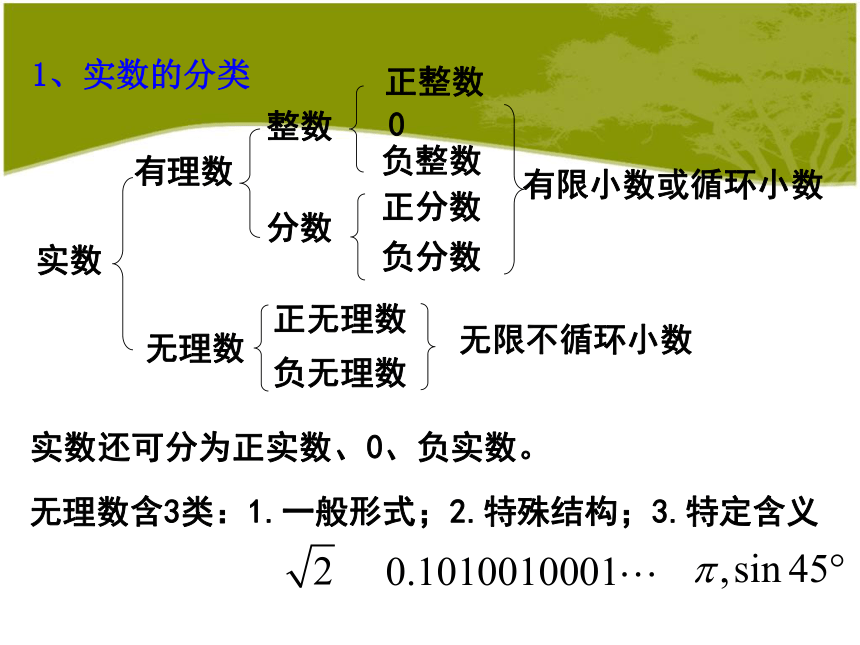
课件21张PPT。第6章 实数1、实数的分类实数整数分数正整数负整数负分数正分数正无理数负无理数有限小数或循环小数无限不循环小数有理数无理数实数还可分为正实数、0、负实数。无理数含3类:1.一般形式;2.特殊结构;3.特定含义0 例1:把下列各数填入相应的集合里 , , 0.353353335…, , , ,cos60°, 0, tan45°, ,
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π0.353353335… , tan45°, ,0, ,π, cos60°,【例2】最小的正整数与最大的负整数之和是_____.02、数轴
◎ 三要素:原点、正方向和单位长度;
◎ 数轴上的点与实数一一对应。3、相反数⑴相反数:只有符号不同的两个数叫做互为相反数,0的相反数是零。
⑵实数 a 的相反数是-a ;在数轴上表示相反数的两点以原点对称。
⑶ a 、b 互为相反数 <==> a + b = 0 4、倒数⑴ a、b互为倒数 <==> ab = 1
a、b互为负倒数 <==> ab =-1
⑵ 0没有倒数.【例1】2010的相反数是_________,
-1.25的倒数是 _________,
的负倒数是_______;-2010【例2】3的相反数的倒数是_________.5、绝对值(1)一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值是零。(2)一个数的绝对值表示这个数的点离开原点的距离。(3) 【例1】3的绝对值是___;-|-2|=____; 0的绝对值是___. 3-20【例2】已知|x|=3,|y|=7,x-y<0,则x+y=______.10或4【例3】实数 a,b 的位置如图
化简 |a + b| – |a – b|a0b【解】由数轴可知,a+b<0,a-b<0,从而
原式=-(a+b)-〔-(a-b)〕
= -a-b+(a-b)
= -a-b+(a-b)
= -a-b+a-b
= -2b【例4】当a<0时,化简 的结果是( )
A 0 B -1 C 1 D ?
【例5】若|a-3|=3-a, 则a的取值范围是( )
A a≤3 B a<3 C a≥3 D a>3
AB⑴平方根:如果 ( ),那么x叫做a的平方根,记作 ,其中 叫做a的算术平方根。
正数有两个平方根,它们互为相反数;零的平方根是零(一个)。负数没有平方根。⑵立方根:如果 (a为一切实数),那么x叫做a的立方根(三次方根), 记作 。
正数有一个正的立方根;零的立方根是零;负数有一个负的立方根。⑶ 6、方根的概念【例1】0.16的平方根是 ;
的算术平方根是 ; 【例2】已知 ,
化简 . 【例3】一个数等于其倒数的4倍,该数为_____.±2【例4】 的平方根是________, 的平方根是________.◎下列各组数,互为相反数的( )
A 2和 B(-1)2和1 C -1和(-1)2 D 2和|-2|
◎ 的相反数是( )
A B - C D –
◎下列各组数中,互为相反数的为( )
A B
C D CCA7、有关实数的非负性(1)任何非负数的和仍是非负数;
(2)若几个非负数的和是0,那么这几个非负数均为0.【例1】若 ,
则 . 【例2】[02潍坊]若 与 互为相反数,
则 的值为 。8、科学记数法 把一个数记成 的形式,其 ,n 为整数。这种记数方法叫做科学记数法。 一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
这时,从左边第一个非0数字起,到精确的数位止,所有的数字,都叫做这个数的有效数字。9、近似数与有效数字【例1】我国国土面积为9 596 960平方千米,用四舍五 入保留两个有效数字,并用科学记数法表示为 _________平方千米.【例2】卫星绕地球运行的速度(即第一宇宙速度)是 ,则卫星绕地球运行 秒走过的路程≈ 米(结果保留两个有效数字)。 数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。10、比较大小【例1】比较大小(用<排列):【例2】用“<”或“>”填空: ___ , ___11、其他【例1】在下面等式的□内填数,○内填运算符号,使等式成立(两个等式的运算符号不能相同) □○□=-9, □○□=-9【例2】写出两个大于1小于4的无理数____、____.【例3】 的整数部分为____.【例4】找规律填表.A 无限小数是无理数
B 绝对值等于本身的数是正数
C 实数和数轴上的点一一对应
D 带根号的数是无理数【例5】下列叙述正确的是( )C【例6】下列说法中,错误的个数是 ( )①无理数都是无限小数;
②无理数都是开方开不尽的数;
③带根号的都是无理数;
④无限小数都是无理数。A.1个 B.2个 C.3个 D.4个C【例7】数轴上的点与( )一一对应.A.整数 B.有理数 C.无理数 D.实数D【例8】相反数是本身的数是 ;绝对值是本身的数 是 ;倒数是本身的数是 .0非负数±1【例9】a、b互为相反数,c与d互为倒数, 则a+1+b+cd= .2【例10】 的绝对值为__________.【例11】找规律,并用公式表示出来.⑴要注意绝对值概念的正确应用。因为互为相反数的绝对值相等,因此绝对值等于一个正数的数有两个,它们是一对互为相反数,不可漏掉其中任何一个。 ⑵解涉及有理数的绝对值、大小比较等问题时,数轴是一个十分有效的工具。可由已知条件确定对应于数轴上的点,按“表示在数轴上的点的数,左边的数总比左边的大”进行比较大小;有时也可采用特殊值法进行判断。【小结】⑶注意平方根与算术平方根的区别与关系。要求一个的平方根或算术平方根,须将这个数先进行化简或计算。⑷相反数和倒数是两个重要的概念,要注意两者的区别。 ⑸已知条件是含有字母的二次根式,要注意隐含的条件,因为 中 ,一般遇到 可转化为 去处理。 作业同步练习
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π0.353353335… , tan45°, ,0, ,π, cos60°,【例2】最小的正整数与最大的负整数之和是_____.02、数轴
◎ 三要素:原点、正方向和单位长度;
◎ 数轴上的点与实数一一对应。3、相反数⑴相反数:只有符号不同的两个数叫做互为相反数,0的相反数是零。
⑵实数 a 的相反数是-a ;在数轴上表示相反数的两点以原点对称。
⑶ a 、b 互为相反数 <==> a + b = 0 4、倒数⑴ a、b互为倒数 <==> ab = 1
a、b互为负倒数 <==> ab =-1
⑵ 0没有倒数.【例1】2010的相反数是_________,
-1.25的倒数是 _________,
的负倒数是_______;-2010【例2】3的相反数的倒数是_________.5、绝对值(1)一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值是零。(2)一个数的绝对值表示这个数的点离开原点的距离。(3) 【例1】3的绝对值是___;-|-2|=____; 0的绝对值是___. 3-20【例2】已知|x|=3,|y|=7,x-y<0,则x+y=______.10或4【例3】实数 a,b 的位置如图
化简 |a + b| – |a – b|a0b【解】由数轴可知,a+b<0,a-b<0,从而
原式=-(a+b)-〔-(a-b)〕
= -a-b+(a-b)
= -a-b+(a-b)
= -a-b+a-b
= -2b【例4】当a<0时,化简 的结果是( )
A 0 B -1 C 1 D ?
【例5】若|a-3|=3-a, 则a的取值范围是( )
A a≤3 B a<3 C a≥3 D a>3
AB⑴平方根:如果 ( ),那么x叫做a的平方根,记作 ,其中 叫做a的算术平方根。
正数有两个平方根,它们互为相反数;零的平方根是零(一个)。负数没有平方根。⑵立方根:如果 (a为一切实数),那么x叫做a的立方根(三次方根), 记作 。
正数有一个正的立方根;零的立方根是零;负数有一个负的立方根。⑶ 6、方根的概念【例1】0.16的平方根是 ;
的算术平方根是 ; 【例2】已知 ,
化简 . 【例3】一个数等于其倒数的4倍,该数为_____.±2【例4】 的平方根是________, 的平方根是________.◎下列各组数,互为相反数的( )
A 2和 B(-1)2和1 C -1和(-1)2 D 2和|-2|
◎ 的相反数是( )
A B - C D –
◎下列各组数中,互为相反数的为( )
A B
C D CCA7、有关实数的非负性(1)任何非负数的和仍是非负数;
(2)若几个非负数的和是0,那么这几个非负数均为0.【例1】若 ,
则 . 【例2】[02潍坊]若 与 互为相反数,
则 的值为 。8、科学记数法 把一个数记成 的形式,其 ,n 为整数。这种记数方法叫做科学记数法。 一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
这时,从左边第一个非0数字起,到精确的数位止,所有的数字,都叫做这个数的有效数字。9、近似数与有效数字【例1】我国国土面积为9 596 960平方千米,用四舍五 入保留两个有效数字,并用科学记数法表示为 _________平方千米.【例2】卫星绕地球运行的速度(即第一宇宙速度)是 ,则卫星绕地球运行 秒走过的路程≈ 米(结果保留两个有效数字)。 数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。10、比较大小【例1】比较大小(用<排列):【例2】用“<”或“>”填空: ___ , ___11、其他【例1】在下面等式的□内填数,○内填运算符号,使等式成立(两个等式的运算符号不能相同) □○□=-9, □○□=-9【例2】写出两个大于1小于4的无理数____、____.【例3】 的整数部分为____.【例4】找规律填表.A 无限小数是无理数
B 绝对值等于本身的数是正数
C 实数和数轴上的点一一对应
D 带根号的数是无理数【例5】下列叙述正确的是( )C【例6】下列说法中,错误的个数是 ( )①无理数都是无限小数;
②无理数都是开方开不尽的数;
③带根号的都是无理数;
④无限小数都是无理数。A.1个 B.2个 C.3个 D.4个C【例7】数轴上的点与( )一一对应.A.整数 B.有理数 C.无理数 D.实数D【例8】相反数是本身的数是 ;绝对值是本身的数 是 ;倒数是本身的数是 .0非负数±1【例9】a、b互为相反数,c与d互为倒数, 则a+1+b+cd= .2【例10】 的绝对值为__________.【例11】找规律,并用公式表示出来.⑴要注意绝对值概念的正确应用。因为互为相反数的绝对值相等,因此绝对值等于一个正数的数有两个,它们是一对互为相反数,不可漏掉其中任何一个。 ⑵解涉及有理数的绝对值、大小比较等问题时,数轴是一个十分有效的工具。可由已知条件确定对应于数轴上的点,按“表示在数轴上的点的数,左边的数总比左边的大”进行比较大小;有时也可采用特殊值法进行判断。【小结】⑶注意平方根与算术平方根的区别与关系。要求一个的平方根或算术平方根,须将这个数先进行化简或计算。⑷相反数和倒数是两个重要的概念,要注意两者的区别。 ⑸已知条件是含有字母的二次根式,要注意隐含的条件,因为 中 ,一般遇到 可转化为 去处理。 作业同步练习
