2021-2022学年华东师大版七年级数学下册9.1.3三角形的三边关系 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学下册9.1.3三角形的三边关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 884.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 09:25:15 | ||
图片预览






文档简介
(共27张PPT)
§9.1.3三角形的三边关系
华东师大版七年级数学下册
1.画一个三角形,使它的三边长分别为
4cm、3cm、2.5cm.
2.三角形的三边之间有什么样的关系?
3.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
4.三角形是否具有稳定性?四边形呢?
本节课要完成的任务(学习目标):
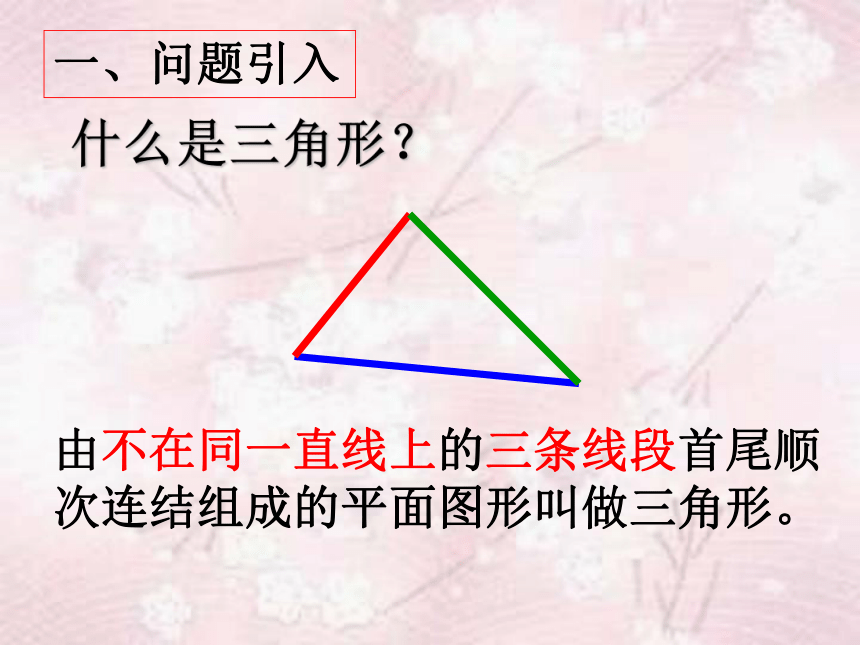
什么是三角形?
由不在同一直线上的三条线段首尾顺次连结组成的平面图形叫做三角形。
一、问题引入
二.猜想探究新知
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5CM长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
(活动一)
(活动二)
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
问题
请同学们任选三条线段画三角形,使它的三条边长分别为你选的三条线段的长,通过所画结果说说你的猜想:
大胆猜测:
两边的长度和与第三边的长度存在什么关系时,就能围成三角形呢?
2
2
4
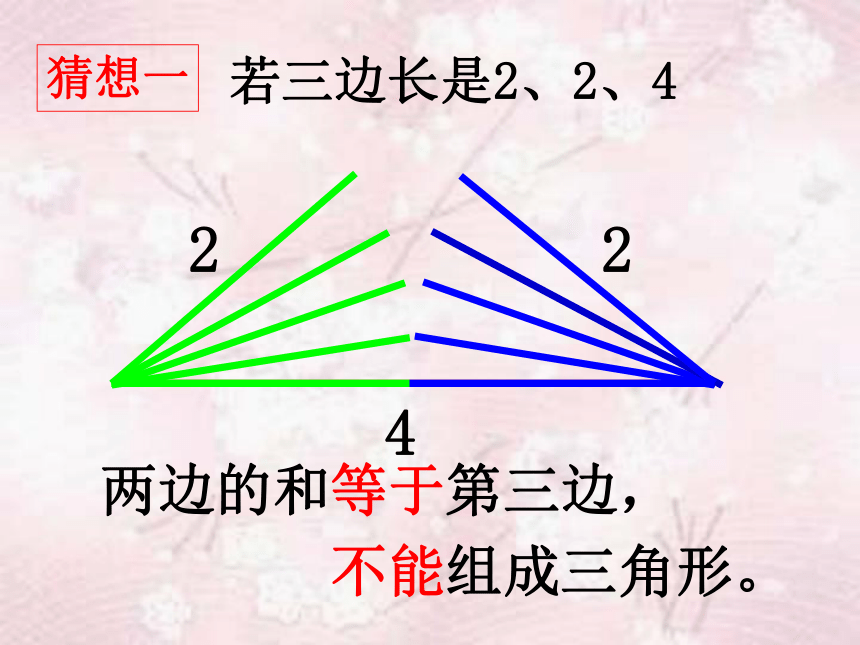
若三边长是2、2、4
猜想一
两边的和等于第三边,
不能组成三角形。
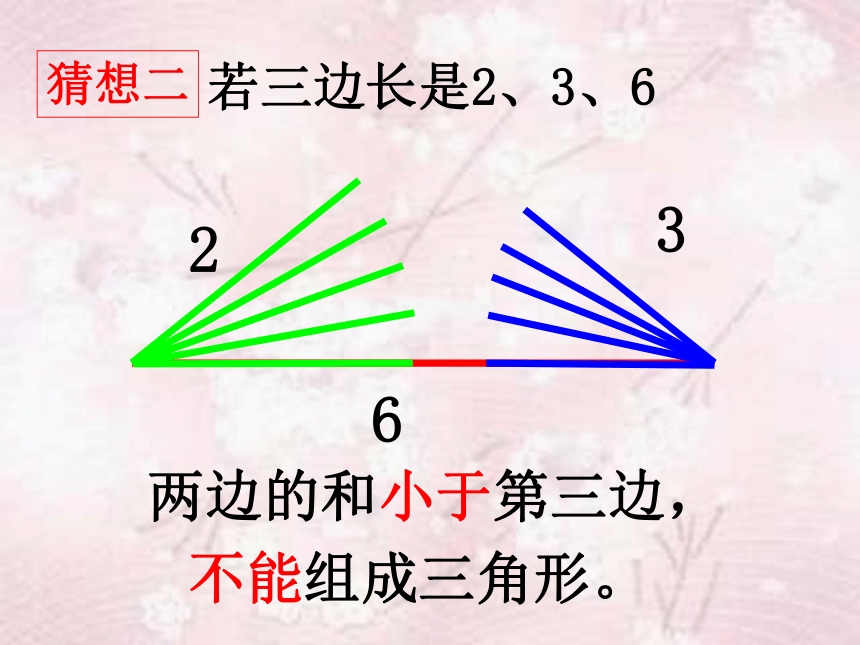
两边的和小于第三边,
不能组成三角形。
2
3
6
若三边长是2、3、6
猜想二
4
5
6
两边的和大于第三边,
能组成三角形。
若三边长是4、5、6
猜想三
两边的和大于第三边,能围成三角形。
结论
a
b
A
B
C
c
换句话说:三角形的任意两边的和大于第三边
问题:这一结论的根本依据是什么?
线段的基本事实:两点之间,线段最短
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
探究一
探究二
△ABC中,
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
三角形的任何两边的差小于第三边.
a
b
A
B
C
c
例1. 以长度为6cm、4cm、3cm 的三条线段能否组成一个三角形?
三.新知应用
若较小的两条线段之和大于第三条线段,便可组成三角形;
若不满足,则不能组成三角形.
如何判断三条已知线段能否组成三角形?
归纳总结
下列长度的各组线段能否组成一个三角形?(口答)
(2) 4cm、5cm、 10cm
(1)15cm、10cm、7cm
(3) 3cm、8cm、 5cm
(4) 4cm、5cm、 6cm
针对练习
现有两根木条a和b,a长10cm,b长 3cm,如果再找一根木条钉成一个三角形木框,那么 对第三根木条c的长度有什么要求?
分析: 如果设木条c的长为xcm,那么仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足x<10+3和 x>10-3。
即{
解得,7 < x < 13
答:第三根木条的长度应在7㎝和13㎝之间。
例2、
在我校有说大话的同学,说自己步子大,一步能走4米多,你相信吗?说说你的理由!
考考你!
四.拓展练习
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
变式训练
1、将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
没有改变
实验
2、将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
易变形
实验
3、在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
不易变形
三角形具有稳定性:
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性。
生活中的三角形
1.三角形的三边之间有什么样的关系?
三角形的任何两边之和大于第三边。
2.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
3.三角形是否具有稳定性?四边形呢?
三角形的任何两边之和大于第三边。
应该以较小的两边的和与较长边进行比较。
三角形具有稳定性,四边形不具有稳定性。
五.小结深化
六.作业设计
A组:课本第82页习题2、3、4;
B组:思考题
从中任选三条,一共有多少组?能组成三角形的有几组?
三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
谢谢指导!
§9.1.3三角形的三边关系
华东师大版七年级数学下册
1.画一个三角形,使它的三边长分别为
4cm、3cm、2.5cm.
2.三角形的三边之间有什么样的关系?
3.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
4.三角形是否具有稳定性?四边形呢?
本节课要完成的任务(学习目标):
什么是三角形?
由不在同一直线上的三条线段首尾顺次连结组成的平面图形叫做三角形。
一、问题引入
二.猜想探究新知
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5CM长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
(活动一)
(活动二)
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
问题
请同学们任选三条线段画三角形,使它的三条边长分别为你选的三条线段的长,通过所画结果说说你的猜想:
大胆猜测:
两边的长度和与第三边的长度存在什么关系时,就能围成三角形呢?
2
2
4
若三边长是2、2、4
猜想一
两边的和等于第三边,
不能组成三角形。
两边的和小于第三边,
不能组成三角形。
2
3
6
若三边长是2、3、6
猜想二
4
5
6
两边的和大于第三边,
能组成三角形。
若三边长是4、5、6
猜想三
两边的和大于第三边,能围成三角形。
结论
a
b
A
B
C
c
换句话说:三角形的任意两边的和大于第三边
问题:这一结论的根本依据是什么?
线段的基本事实:两点之间,线段最短
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
探究一
探究二
△ABC中,
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
三角形的任何两边的差小于第三边.
a
b
A
B
C
c
例1. 以长度为6cm、4cm、3cm 的三条线段能否组成一个三角形?
三.新知应用
若较小的两条线段之和大于第三条线段,便可组成三角形;
若不满足,则不能组成三角形.
如何判断三条已知线段能否组成三角形?
归纳总结
下列长度的各组线段能否组成一个三角形?(口答)
(2) 4cm、5cm、 10cm
(1)15cm、10cm、7cm
(3) 3cm、8cm、 5cm
(4) 4cm、5cm、 6cm
针对练习
现有两根木条a和b,a长10cm,b长 3cm,如果再找一根木条钉成一个三角形木框,那么 对第三根木条c的长度有什么要求?
分析: 如果设木条c的长为xcm,那么仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足x<10+3和 x>10-3。
即{
解得,7 < x < 13
答:第三根木条的长度应在7㎝和13㎝之间。
例2、
在我校有说大话的同学,说自己步子大,一步能走4米多,你相信吗?说说你的理由!
考考你!
四.拓展练习
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
变式训练
1、将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
没有改变
实验
2、将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
易变形
实验
3、在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
不易变形
三角形具有稳定性:
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性。
生活中的三角形
1.三角形的三边之间有什么样的关系?
三角形的任何两边之和大于第三边。
2.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
3.三角形是否具有稳定性?四边形呢?
三角形的任何两边之和大于第三边。
应该以较小的两边的和与较长边进行比较。
三角形具有稳定性,四边形不具有稳定性。
五.小结深化
六.作业设计
A组:课本第82页习题2、3、4;
B组:思考题
从中任选三条,一共有多少组?能组成三角形的有几组?
三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
谢谢指导!
