人教A版必修三 2.2.1用样本的频率分布估计总体分布 课件(共25张PPT)
文档属性
| 名称 | 人教A版必修三 2.2.1用样本的频率分布估计总体分布 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 374.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 16:01:05 | ||
图片预览





文档简介
(共25张PPT)
2.2.1用样本的频率分布估计总体分布
探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费.
如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢?为了较为合理地确定出这个标准,你认为需要做哪些工作?
提出问题
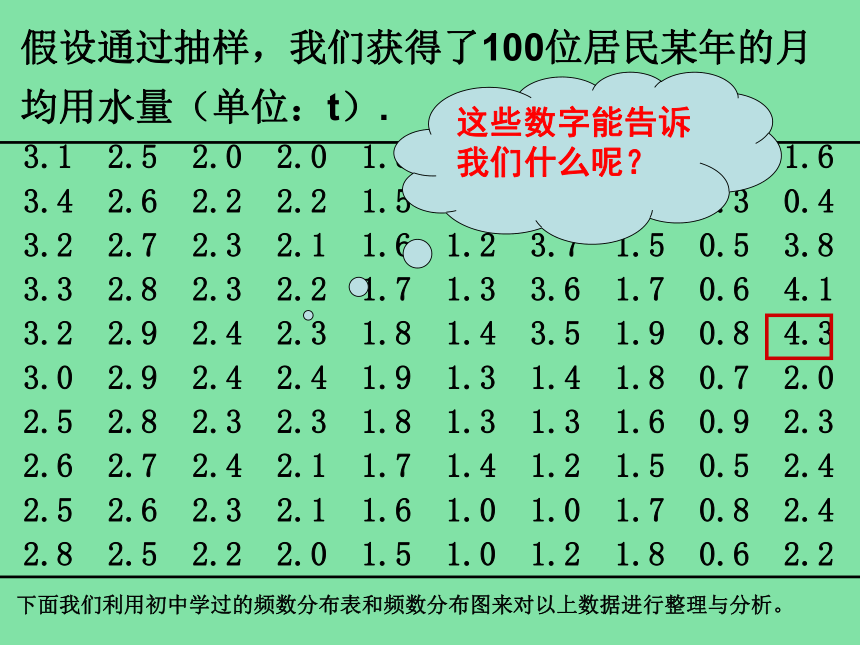
假设通过抽样,我们获得了100位居民某年的月均用水量(单位:t).
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
下面我们利用初中学过的频数分布表和频数分布图来对以上数据进行整理与分析。
这些数字能告诉我们什么呢?
频数:
复习旧知
问题:什么是频数 画频数分布直方图的一般步骤是什么?
画频数分布直方图的一般步骤是:
1.计算最大值与最小值的差
2.决定组距和组数
3.将数据分组
4.列频数分布表
5.画频数分布直方图
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数叫做频数.
1.求极差(即计算最大值与最小值的差)
2.决定组距和组数
3.将数据分组
4.3-0.2=4.1
组数=
最大值-最小值
组距
= = 8.2
4.1
0.5
[0,0.5),[0.5,1),[1,1.5),…,[4,4.5]
取组距为0.5
下面我们画出频数分布直方图来对以上数据进行分析。
组数为9
分组 频数累计 频数
[0,0.5)
[0.5,1)
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
4
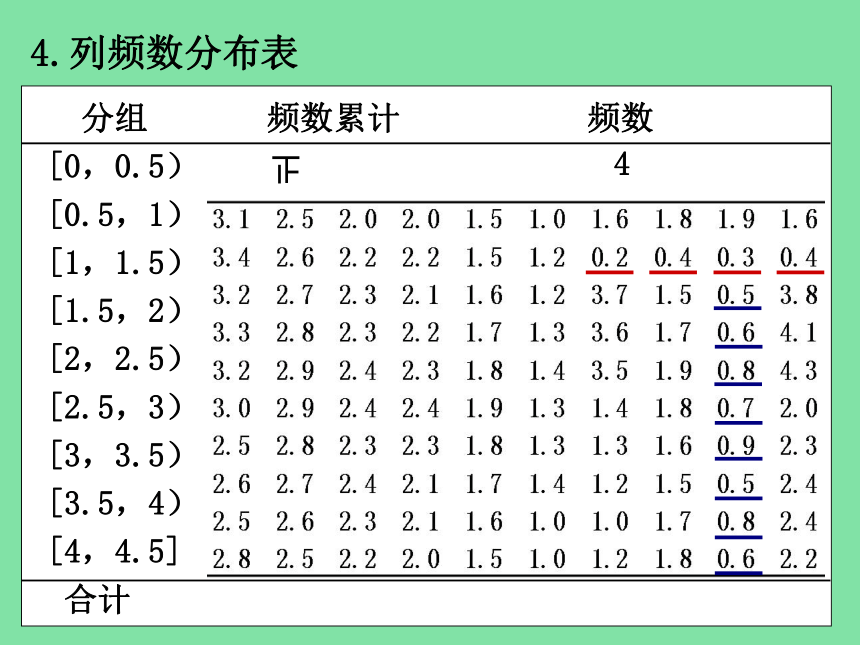
4.列频数分布表
分组 频数累计 频数
[0,0.5)
[0.5,1) 正
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
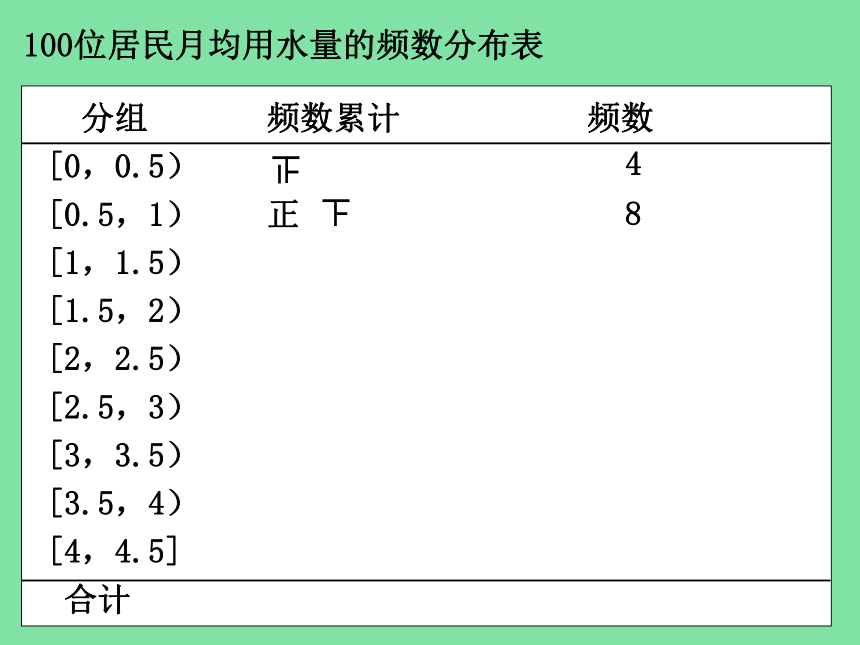
100位居民月均用水量的频数分布表
4
8
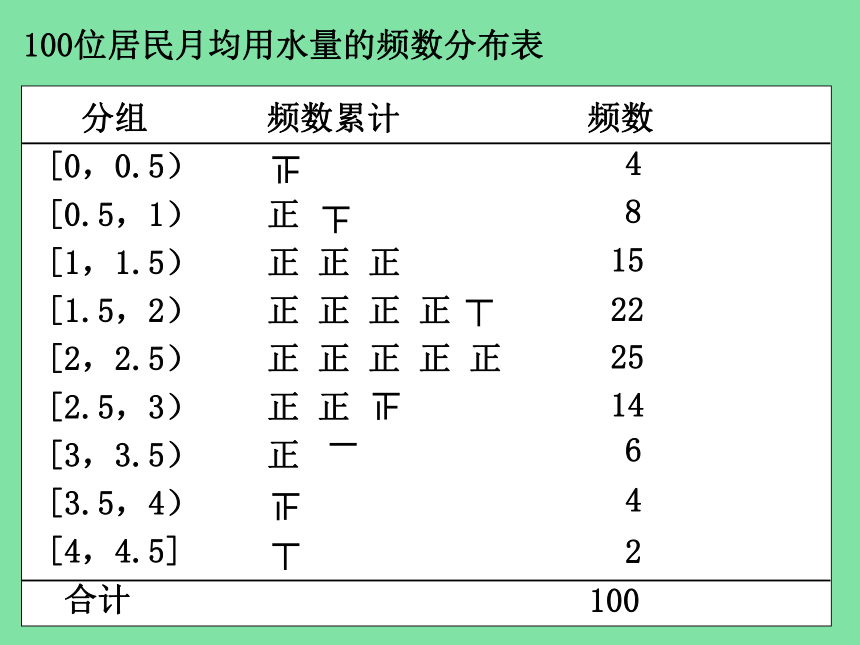
分组 频数累计 频数
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频数分布表
频数
月平均用水量/t
25
20
15
10
5
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月均用水量的频数分布直方图
5.画频数分布直方图
能够清楚地知道数据分布在各个小组的个数
从各个小组数据在样本容量中所占比例大小的角度,来表示数据分布的规律.
学习新知 (一):频率分布表
第N组的频率=
第N组频数
样本容量
样本数据的频率分布
什么是频率呢?
分组 频数累计 频数 频率
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频数分布表
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1.00
分组 频数累计 频数 频率
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频率分布表
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1.00
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
100位居民月均用水量的频率分布表
频数
月平均用水量/t
25
20
15
10
5
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月均用水量的频数分布直方图
频率/组距
分组 频数 频率 频率/组距
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
0.08
0.16
0.30
0.44
0.50
0.28
0.12
0.08
0.04
100位居民月均用水量的频率分布表
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
学习新知(二):频率分布直方图
100位居民月均用水量的频率分布直方图
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考:频率分布直方图中各小长方形的面积表示什么?各小长方形的面积总和为多少?
小长方形的面积=
组距X
组距
频率
=频率
样本容量
频数
=
方法归纳:对一组给定的样本数据,频率分布直方图的画法
第一步,求极差
第二步,决定组距与组数
第三步,将数据分组
第四步,列频率分布表
第五步,画频率分布直方图
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考3:你能根据上述频率分布表和频率分布直方图指出居民月均用水量的一些数据特点吗?
应用新知
显示了样本数据落在各个小组的比例大小
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考4:如果当地政府希望使85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗?
大约有88%的居民月用水量在3t以下,可建议取a=3t.
频率分布折线图
连接频率分布直方图中各个小长方形上端的中点,频率分布折线图
随着样本容量的增加,作图时所分的组数也会增加,相应的频率折线图会越来越接近于一条光滑的曲线,统计学中称这条光滑的曲线为总体密度曲线.
总体密度曲线
统计中称这条光滑曲线为总体密度曲线,它反映了总体在各个范围内取值的百分比.
阴影部分的面积表示总体在区间(a,b)内取值的百分比.
茎叶图
甲乙两名篮球运动员每场比赛得分的原始记录如下:
甲得分:13,51,23,8,26,38,16,33,14,28,39
乙得分:49,24,12,31,50,31,44,36,15,37,25,36,39
0
1
2
3
4
5
甲
乙
3
4
6
8
3
6
9
3
8
8
1
2
5
5
4
1
6
1
6
7
9
4
9
0
样本数据的茎叶图的步骤:
第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;
第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在中间;
第三步,将各个数据的叶按大小次序写在茎右(左)侧.
思考7: 频率分布直方图有什么优点和缺点?
优点:直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式.
缺点:直方图丢失了一些信息,原始数据不能在图中表示出来.
合作交流
总结反思
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
各小长方形的面积(之和)表示相应各组的频率(之和)
2.2.1用样本的频率分布估计总体分布
探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费.
如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢?为了较为合理地确定出这个标准,你认为需要做哪些工作?
提出问题
假设通过抽样,我们获得了100位居民某年的月均用水量(单位:t).
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
下面我们利用初中学过的频数分布表和频数分布图来对以上数据进行整理与分析。
这些数字能告诉我们什么呢?
频数:
复习旧知
问题:什么是频数 画频数分布直方图的一般步骤是什么?
画频数分布直方图的一般步骤是:
1.计算最大值与最小值的差
2.决定组距和组数
3.将数据分组
4.列频数分布表
5.画频数分布直方图
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数叫做频数.
1.求极差(即计算最大值与最小值的差)
2.决定组距和组数
3.将数据分组
4.3-0.2=4.1
组数=
最大值-最小值
组距
= = 8.2
4.1
0.5
[0,0.5),[0.5,1),[1,1.5),…,[4,4.5]
取组距为0.5
下面我们画出频数分布直方图来对以上数据进行分析。
组数为9
分组 频数累计 频数
[0,0.5)
[0.5,1)
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
4
4.列频数分布表
分组 频数累计 频数
[0,0.5)
[0.5,1) 正
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
100位居民月均用水量的频数分布表
4
8
分组 频数累计 频数
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频数分布表
频数
月平均用水量/t
25
20
15
10
5
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月均用水量的频数分布直方图
5.画频数分布直方图
能够清楚地知道数据分布在各个小组的个数
从各个小组数据在样本容量中所占比例大小的角度,来表示数据分布的规律.
学习新知 (一):频率分布表
第N组的频率=
第N组频数
样本容量
样本数据的频率分布
什么是频率呢?
分组 频数累计 频数 频率
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频数分布表
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1.00
分组 频数累计 频数 频率
[0,0.5)
[0.5,1) 正
[1,1.5) 正 正 正
[1.5,2) 正 正 正 正
[2,2.5) 正 正 正 正 正
[2.5,3) 正 正
[3,3.5) 正
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
100
100位居民月均用水量的频率分布表
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1.00
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
100位居民月均用水量的频率分布表
频数
月平均用水量/t
25
20
15
10
5
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月均用水量的频数分布直方图
频率/组距
分组 频数 频率 频率/组距
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
0.08
0.16
0.30
0.44
0.50
0.28
0.12
0.08
0.04
100位居民月均用水量的频率分布表
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
学习新知(二):频率分布直方图
100位居民月均用水量的频率分布直方图
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考:频率分布直方图中各小长方形的面积表示什么?各小长方形的面积总和为多少?
小长方形的面积=
组距X
组距
频率
=频率
样本容量
频数
=
方法归纳:对一组给定的样本数据,频率分布直方图的画法
第一步,求极差
第二步,决定组距与组数
第三步,将数据分组
第四步,列频率分布表
第五步,画频率分布直方图
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考3:你能根据上述频率分布表和频率分布直方图指出居民月均用水量的一些数据特点吗?
应用新知
显示了样本数据落在各个小组的比例大小
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
思考4:如果当地政府希望使85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗?
大约有88%的居民月用水量在3t以下,可建议取a=3t.
频率分布折线图
连接频率分布直方图中各个小长方形上端的中点,频率分布折线图
随着样本容量的增加,作图时所分的组数也会增加,相应的频率折线图会越来越接近于一条光滑的曲线,统计学中称这条光滑的曲线为总体密度曲线.
总体密度曲线
统计中称这条光滑曲线为总体密度曲线,它反映了总体在各个范围内取值的百分比.
阴影部分的面积表示总体在区间(a,b)内取值的百分比.
茎叶图
甲乙两名篮球运动员每场比赛得分的原始记录如下:
甲得分:13,51,23,8,26,38,16,33,14,28,39
乙得分:49,24,12,31,50,31,44,36,15,37,25,36,39
0
1
2
3
4
5
甲
乙
3
4
6
8
3
6
9
3
8
8
1
2
5
5
4
1
6
1
6
7
9
4
9
0
样本数据的茎叶图的步骤:
第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;
第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在中间;
第三步,将各个数据的叶按大小次序写在茎右(左)侧.
思考7: 频率分布直方图有什么优点和缺点?
优点:直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式.
缺点:直方图丢失了一些信息,原始数据不能在图中表示出来.
合作交流
总结反思
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
各小长方形的面积(之和)表示相应各组的频率(之和)
