22.3实际问题与二次函数(3)课件 (共27张PPT)
文档属性
| 名称 | 22.3实际问题与二次函数(3)课件 (共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 13:04:29 | ||
图片预览



文档简介
(共27张PPT)
人教版 九年级上册
22.3实际问题与二次函数(3)
抛物线型建筑物问题
x
y
O
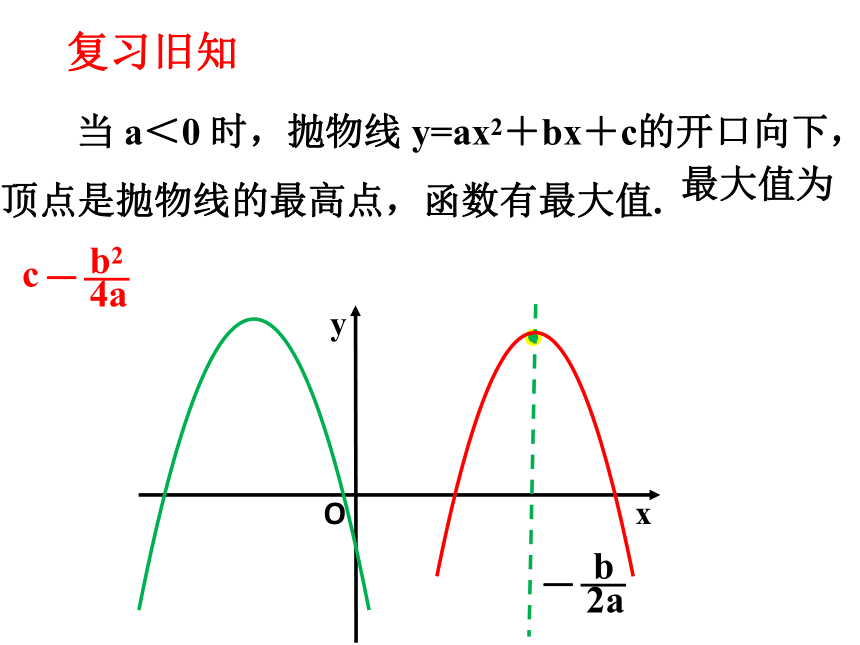
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
-
b
2a
-
最大值为
复习旧知
x
y
O
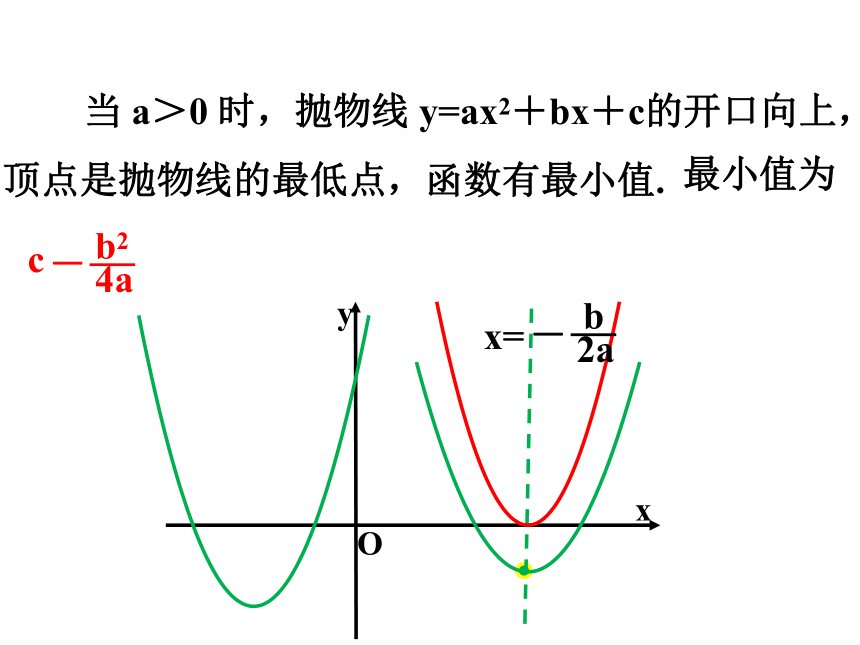
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
b
2a
-
x=
c
b2
4a
-
最小值为
解:
∴ 这条抛物线有最低点,
∴x =
b
2a
-
=
∴它的最低点坐标为(-2,-1).
2
2×
=-2
-
y=
=-1
∴ 这条抛物线开口向上,
∵ b=2 ,c=1,
c
b2
4a
-
=
22
4×
1-
∵ a= > 0 ,
求下列抛物线最高点或最低点的坐标.
① y = x2+2x+1, ② y =- x2+x-4
1
2
1
4
①
1
2
1
2
1
2
求下列抛物线最高点或最低点的坐标.
① y = x2+2x+1, ② y =- x2+x-4
解:
∴ 这条抛物线有最高点,
∴x =
b
2a
-
=
∴它的最高点坐标为( 2,3 ).
∵ a=- <0 ,
1
2×(- )
=2
y=
=3
∴ 这条抛物线开口向下,
∵ b=1 ,c=-4,
c
b2
4a
-
=
12
4×(- )
-4-
-
1
2
1
4
②
1
4
1
4
1
4
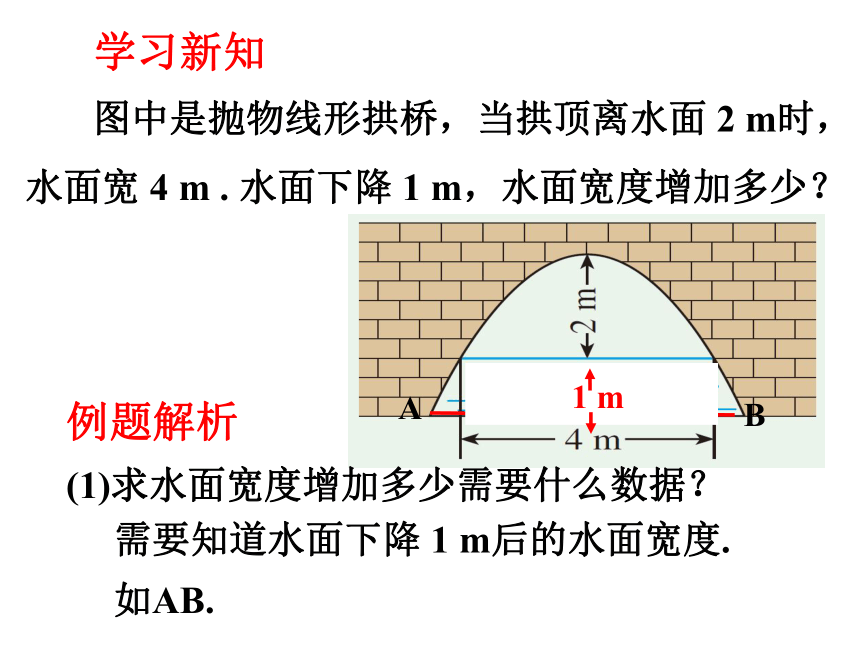
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 1 m后的水面宽度.
A
B
如AB.
学习新知
例题解析
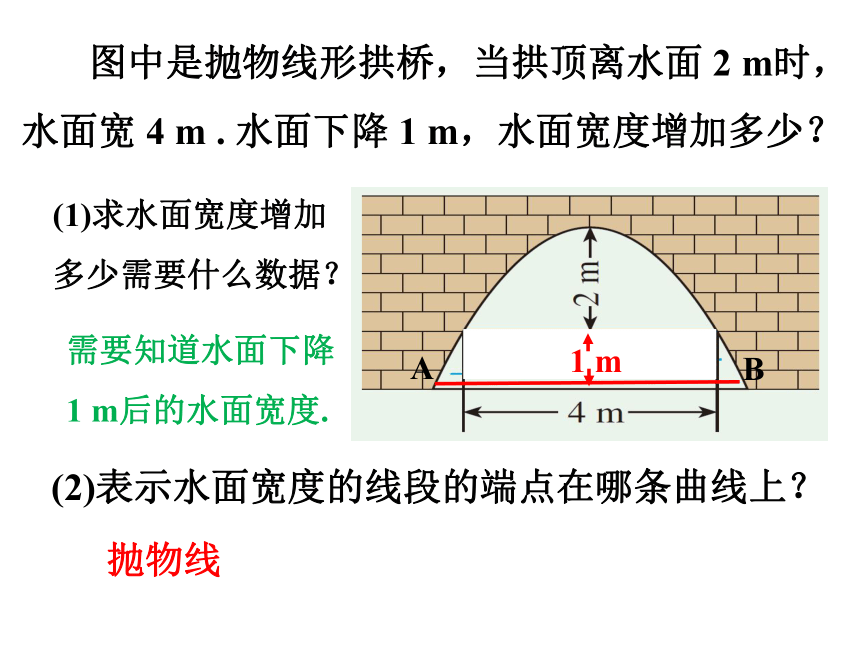
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 1 m后的水面宽度.
A
B
(2)表示水面宽度的线段的端点在哪条曲线上?
抛物线
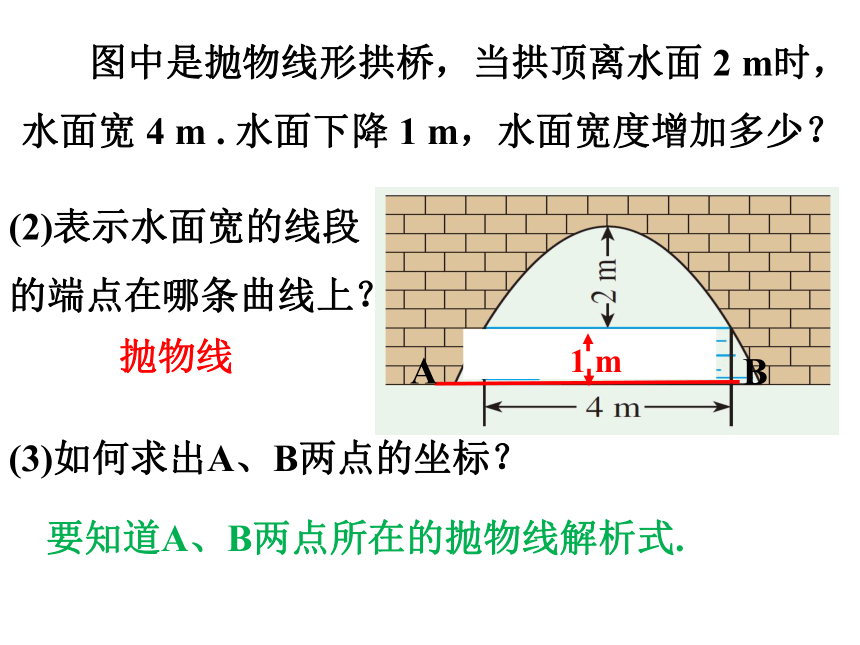
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
A
B
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求出A、B两点的坐标?
要知道A、B两点所在的抛物线解析式.
抛物线
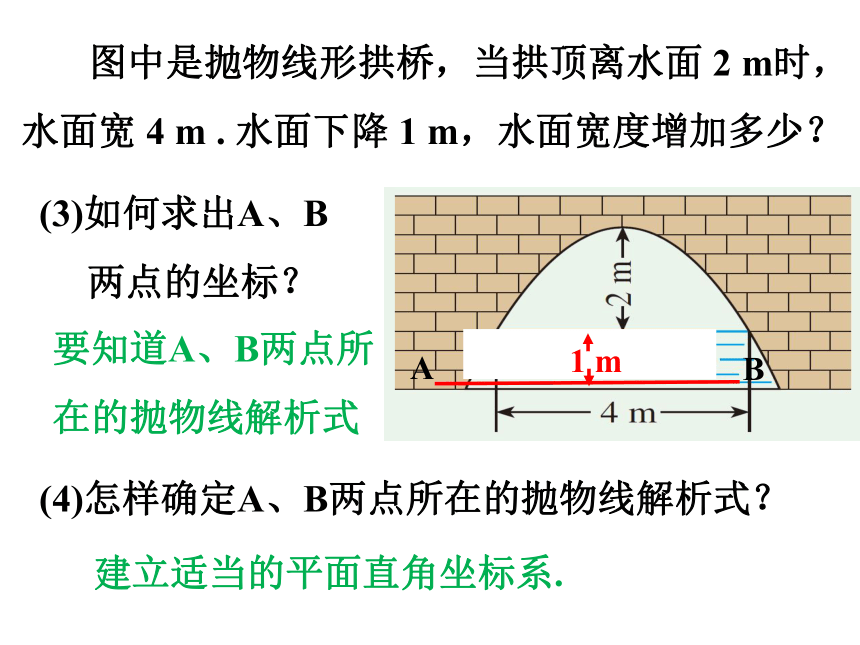
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
A
B
(3)如何求出A、B
两点的坐标?
(4)怎样确定A、B两点所在的抛物线解析式?
要知道A、B两点所在的抛物线解析式
建立适当的平面直角坐标系.
(5)如何建立直角坐标系?
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
(4)怎样确定A、B两点
所在的抛物线解析式?
建立适当的坐标系.
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系.
x
y
O
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
以抛物线的顶点为原点,以抛物线的对称轴
为y轴建立直角坐标系.
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
设抛物线的解析式为y=ax2.
(2,-2)
C
D
拱顶离水面 2 m
E
水面宽 4 m
即OE=2
即CD=4
∴ ED=2
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
设抛物线的解析式为y=ax2.
∵抛物线经过点(2,-2).
∴-2=a×22.
∴a=- .
∴抛物线的解析式为y=- x2.
∵当水面下降 1 m时,
水面的纵坐标为-3,
即y=-3.
∴-3=- x2
1
2
1
2
1
2
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
(2,-2)
C
D
解:
设抛物线的解析式为y=ax2.
∵抛物线经过点(2,-2),
∴-2=a×22.
∴a=- .
∴抛物线的解析式为y=- x2.
当水面下降 1 m时,
水面的纵坐标为3,
即y=-3.
∴-3=- x2,
∴x1=- ,
x2= .
∴AB=
水面下降 1 m时,
水面宽度增加 m.
( -4)
1
2
6
6
6
2
6
2
1
2
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
(2,-2)
C
D
1
2
解:
建立适当坐标系解决实际问题的一般步骤:
(1)建立适当的直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数的表达式;
(4)代人已知条件或点的坐标,求出函数表达式;
(5)利用函数表达式求解问题.
学有所得
根据建立的坐标系选择适当的二次函数表达:
(1)顶点在原点,对称轴是y轴,可设函数表达式
为y=ax2;
(2)对称轴是y轴,可设函数表达式为y=ax2+k;
(3)顶点在x轴,对称轴平行于y轴,可设函数表达式
为y=a(x+h)2;
(4)抛物线过原点,对称轴平行于y轴,可设函数表达
式为y= ax2+bx.
学以致用
x
y
O
1.如图桥拱的形状是抛物线形,其函数表达式是y=- x2.当水面宽为8m时,桥拱顶部到水面的高度是( ).
A.8 m B.6 m C.4 m D. 2 m
1
8
D
2.如图是一个横断面为抛物线形的拱桥,当水面在l时,拱桥(拱桥洞的最高点)离水面2m,水面宽4m.建立如图所示的平面直角坐标系,则抛物线对应的函数表达式为( ).
A.у=-2x B. у=2x C.y=- x2 D.y= x2
1
2
1
2
x
y
O
C
3.设计师以函数y=2x2-4x+8的图象为灵感设计杯子,如图所示.若AB=4,DE=3,则杯子的高 CE=( ).
A.17 B.11 C.8 D.7
A
B
C
D
E
B
4.如图是某座抛物线形廊桥的示意图.已知抛物线的函数表达式为y=- x2+10.为保护廊桥的安全,在该抛物线上距水面AB高为8m的点 E,F处要安装两盏警示灯,则这两盏灯的水平距离 EF是 m.
1
40
x
y
O
A
B
E
F
5
8
5.如图,某工厂车间门口由抛物线和矩形 ABCD的三边组成,门的最大高度是4.9m,AB=10m,BC=2.4m.有一个高4m、宽2m的长方体大型设备要运进车间.如果不考虑其他因素,设备的右侧离门边 m,此设备运进车间时才不致于碰门的顶部.
A
B
C
D
2
6.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m.已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点,则抛物线的函数表达式是
y=- (x-6) +4 ;若选取点B为坐标原点,则抛物线的函数表达是 .
1
9
A
B
12m
4m
y=- (x+6) +4
1
9
(1)这节课学习了用什么知识解决哪类问题?
(2)解决问题的一般步骤是什么?应注意哪些问题?
(3)你学到了哪些思考问题的方法?用函数的思想 方法解决抛物线形拱桥问题应注意什么?
小结
今天作业
课本P52页第3、5题
二次函数是单变量最优化问题的数学模型,如生活中涉及的求最大利润,最大面积等.这体现了数学的实用性,是理论与实践结合的集中体现.本节课主要研究建立坐标系解决实际问题.
课件说明
学习目标: 能够分析和表示实际问题中变量之间的二次函数关系,正确建立坐标系,并运用二次函数的图象、性质解决实际问题.
学习重点: 建立坐标系,利用二次函数的图象、性质解决实际问题.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
22.3实际问题与二次函数(3)
抛物线型建筑物问题
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
-
b
2a
-
最大值为
复习旧知
x
y
O
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
b
2a
-
x=
c
b2
4a
-
最小值为
解:
∴ 这条抛物线有最低点,
∴x =
b
2a
-
=
∴它的最低点坐标为(-2,-1).
2
2×
=-2
-
y=
=-1
∴ 这条抛物线开口向上,
∵ b=2 ,c=1,
c
b2
4a
-
=
22
4×
1-
∵ a= > 0 ,
求下列抛物线最高点或最低点的坐标.
① y = x2+2x+1, ② y =- x2+x-4
1
2
1
4
①
1
2
1
2
1
2
求下列抛物线最高点或最低点的坐标.
① y = x2+2x+1, ② y =- x2+x-4
解:
∴ 这条抛物线有最高点,
∴x =
b
2a
-
=
∴它的最高点坐标为( 2,3 ).
∵ a=- <0 ,
1
2×(- )
=2
y=
=3
∴ 这条抛物线开口向下,
∵ b=1 ,c=-4,
c
b2
4a
-
=
12
4×(- )
-4-
-
1
2
1
4
②
1
4
1
4
1
4
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 1 m后的水面宽度.
A
B
如AB.
学习新知
例题解析
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 1 m后的水面宽度.
A
B
(2)表示水面宽度的线段的端点在哪条曲线上?
抛物线
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
A
B
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求出A、B两点的坐标?
要知道A、B两点所在的抛物线解析式.
抛物线
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
1 m
A
B
(3)如何求出A、B
两点的坐标?
(4)怎样确定A、B两点所在的抛物线解析式?
要知道A、B两点所在的抛物线解析式
建立适当的平面直角坐标系.
(5)如何建立直角坐标系?
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
(4)怎样确定A、B两点
所在的抛物线解析式?
建立适当的坐标系.
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系.
x
y
O
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
以抛物线的顶点为原点,以抛物线的对称轴
为y轴建立直角坐标系.
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
设抛物线的解析式为y=ax2.
(2,-2)
C
D
拱顶离水面 2 m
E
水面宽 4 m
即OE=2
即CD=4
∴ ED=2
图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
设抛物线的解析式为y=ax2.
∵抛物线经过点(2,-2).
∴-2=a×22.
∴a=- .
∴抛物线的解析式为y=- x2.
∵当水面下降 1 m时,
水面的纵坐标为-3,
即y=-3.
∴-3=- x2
1
2
1
2
1
2
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
(2,-2)
C
D
解:
设抛物线的解析式为y=ax2.
∵抛物线经过点(2,-2),
∴-2=a×22.
∴a=- .
∴抛物线的解析式为y=- x2.
当水面下降 1 m时,
水面的纵坐标为3,
即y=-3.
∴-3=- x2,
∴x1=- ,
x2= .
∴AB=
水面下降 1 m时,
水面宽度增加 m.
( -4)
1
2
6
6
6
2
6
2
1
2
x
y
O
1
2
-1
-2
-2
-3
A
B
-1
(2,-2)
C
D
1
2
解:
建立适当坐标系解决实际问题的一般步骤:
(1)建立适当的直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数的表达式;
(4)代人已知条件或点的坐标,求出函数表达式;
(5)利用函数表达式求解问题.
学有所得
根据建立的坐标系选择适当的二次函数表达:
(1)顶点在原点,对称轴是y轴,可设函数表达式
为y=ax2;
(2)对称轴是y轴,可设函数表达式为y=ax2+k;
(3)顶点在x轴,对称轴平行于y轴,可设函数表达式
为y=a(x+h)2;
(4)抛物线过原点,对称轴平行于y轴,可设函数表达
式为y= ax2+bx.
学以致用
x
y
O
1.如图桥拱的形状是抛物线形,其函数表达式是y=- x2.当水面宽为8m时,桥拱顶部到水面的高度是( ).
A.8 m B.6 m C.4 m D. 2 m
1
8
D
2.如图是一个横断面为抛物线形的拱桥,当水面在l时,拱桥(拱桥洞的最高点)离水面2m,水面宽4m.建立如图所示的平面直角坐标系,则抛物线对应的函数表达式为( ).
A.у=-2x B. у=2x C.y=- x2 D.y= x2
1
2
1
2
x
y
O
C
3.设计师以函数y=2x2-4x+8的图象为灵感设计杯子,如图所示.若AB=4,DE=3,则杯子的高 CE=( ).
A.17 B.11 C.8 D.7
A
B
C
D
E
B
4.如图是某座抛物线形廊桥的示意图.已知抛物线的函数表达式为y=- x2+10.为保护廊桥的安全,在该抛物线上距水面AB高为8m的点 E,F处要安装两盏警示灯,则这两盏灯的水平距离 EF是 m.
1
40
x
y
O
A
B
E
F
5
8
5.如图,某工厂车间门口由抛物线和矩形 ABCD的三边组成,门的最大高度是4.9m,AB=10m,BC=2.4m.有一个高4m、宽2m的长方体大型设备要运进车间.如果不考虑其他因素,设备的右侧离门边 m,此设备运进车间时才不致于碰门的顶部.
A
B
C
D
2
6.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m.已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点,则抛物线的函数表达式是
y=- (x-6) +4 ;若选取点B为坐标原点,则抛物线的函数表达是 .
1
9
A
B
12m
4m
y=- (x+6) +4
1
9
(1)这节课学习了用什么知识解决哪类问题?
(2)解决问题的一般步骤是什么?应注意哪些问题?
(3)你学到了哪些思考问题的方法?用函数的思想 方法解决抛物线形拱桥问题应注意什么?
小结
今天作业
课本P52页第3、5题
二次函数是单变量最优化问题的数学模型,如生活中涉及的求最大利润,最大面积等.这体现了数学的实用性,是理论与实践结合的集中体现.本节课主要研究建立坐标系解决实际问题.
课件说明
学习目标: 能够分析和表示实际问题中变量之间的二次函数关系,正确建立坐标系,并运用二次函数的图象、性质解决实际问题.
学习重点: 建立坐标系,利用二次函数的图象、性质解决实际问题.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
