22.3实际问题与二次函数(1) 课件(共27张PPT)
文档属性
| 名称 | 22.3实际问题与二次函数(1) 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
人教版 九年级上册
22.3实际问题与二次函数(1)
最大(或最小)面积问题
若y=ax2+bx+c(a ≠ 0),则y叫做x的二次函数;
二次函数y=ax2+bx+c的图象是一条抛物线;
当a>0时,开口向上;当a<0时,开口向下;
y=ax2+bx+c的对轴是直线x = ;
y=ax2+bx+c顶点坐标为 ( , );
y=ax2+bx+c与y轴的交点坐标为 (0,c) .
b
2a
-
b
2a
-
c
b2
4a
-
复习旧知
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
-
b
2a
-
最大值为
c
b2
4a
-
( , )
b
2a
-
x=
x
y
O
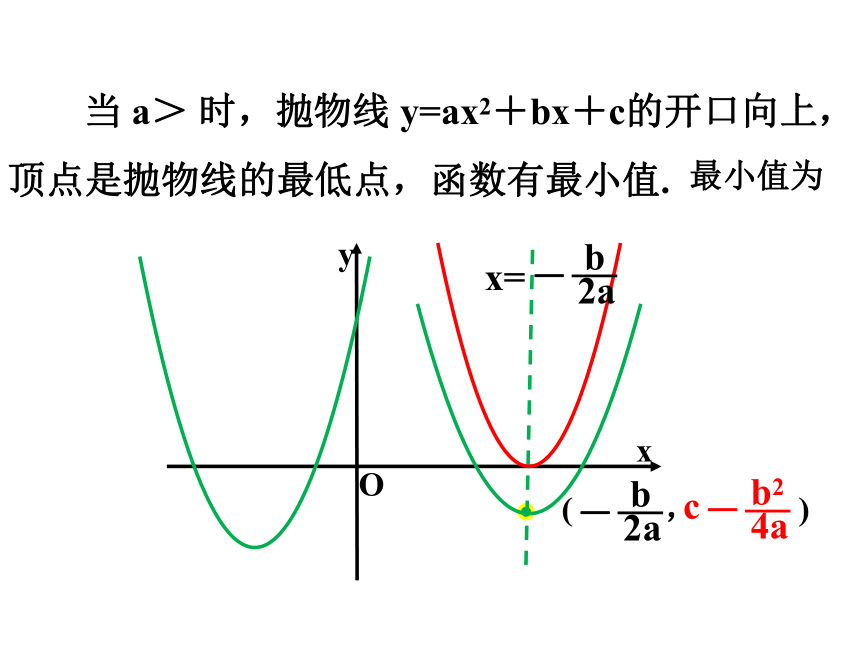
当 a> 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
b
2a
-
x=
c
b2
4a
-
最小值为
( , )
b
2a
-
求出下列抛物线最高点或最低点的坐标.
① y =-4x2+3x, ② y =3x2+x+6
解:
①
∴ 这条抛物线有最高点,
∴x =
b
2a
-
=
∴它的最高点坐标为( , ).
∵ a=-4<0 ,
3
2×(-4)
=
-
3
8
3
8
9
16
y=
=
9
16
∴ 这条抛物线开口向下,
∵ b=3 ,c=0
c
b2
4a
-
=
32
4×(-4)
0-
求出下列抛物线的有最高点或最低点吗?.
① y =-4x2+3x, ② y =3x2+x+6
解:
∴ 这条抛物线有最低点,
∴x =
b
2a
-
=
∴它的最低点坐标为( , ).
1
2×3
=
-
1
6
1
6
71
12
y=
=
71
12
∴ 这条抛物线开口向上,
∵ b=1 ,c=6,
c
b2
4a
-
=
12
4×3
6-
∵ a=3> 0 ,
-
-
②
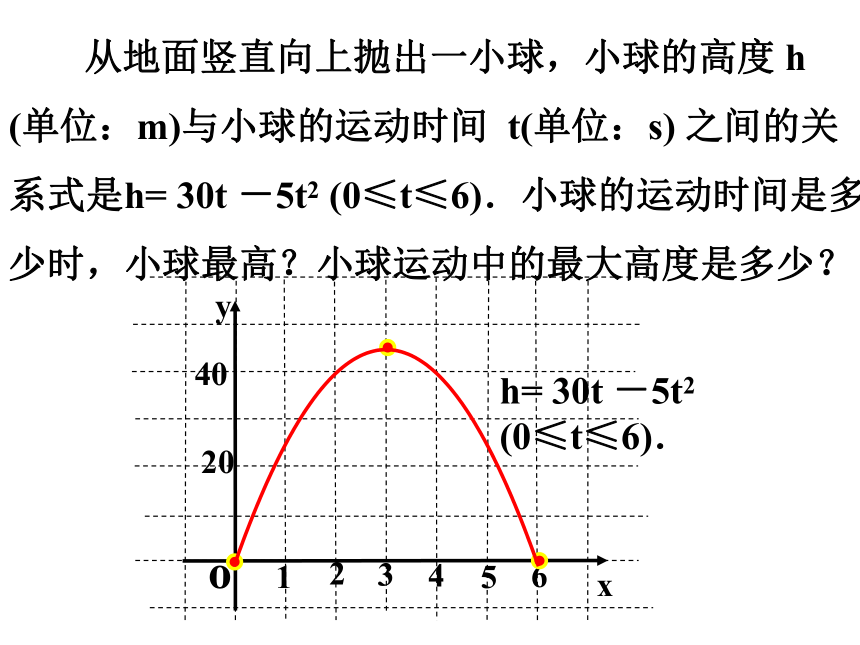
从地面竖直向上抛出一小球,小球的高度 h
(单位:m)与小球的运动时间 t(单位:s) 之间的关系式是h= 30t -5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
x
y
o
1
2
3
4
40
20
5
6
h= 30t -5t2 (0≤t≤6).
x
y
o
1
2
3
4
40
20
5
6
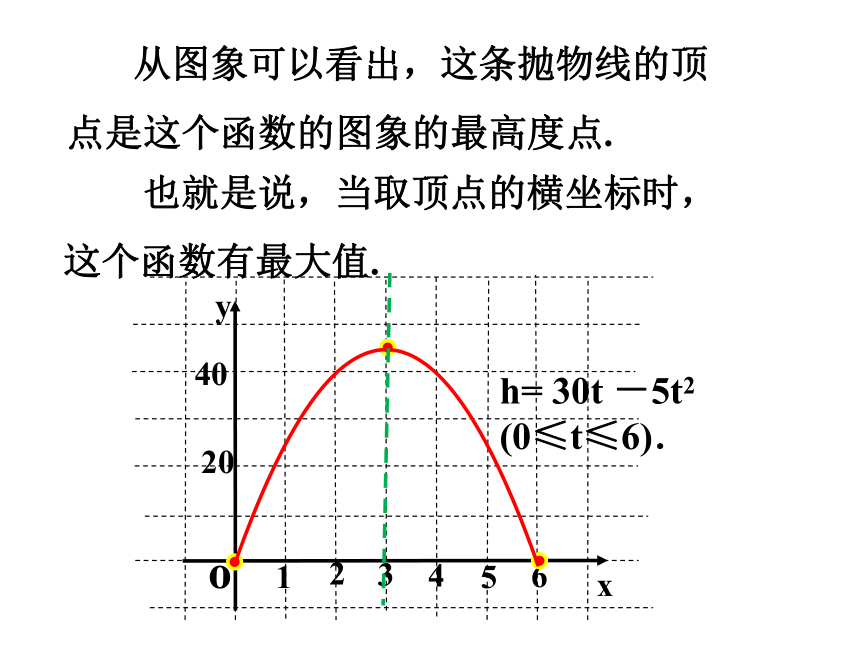
h= 30t -5t2 (0≤t≤6).
从图象可以看出,这条抛物线的顶点是这个函数的图象的最高度点.
也就是说,当取顶点的横坐标时,这个函数有最大值.
从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s) 之间的关系式是
h= 30t -5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
∵ a=-5<0 ,
∵ b=30,
∴ 这个函数有最大值,
当 t=3 时,
h =30×3-5×32
=
∵当 t= 时,
b
2a
-
h有最大值.
∴
t=
b
2a
-
=
-
30
2×(-5)
=3
45
∵ a=-5<0 ,
∵ b=30,
∴ 这个函数有最大值,
当 t=3 时,
h =30×3-5×32
=
∵当 t= 时,
b
2a
-
h有最大值.
∴t=
b
2a
-
=
-
30
2×(-5)
=3
45
∴小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
当a<0 ,抛物线 y = ax2+bx+c 的顶点是最高点,
即二次函数 y = ax2+bx+c 有最大值.
如何求出二次函数 y = ax2+bx+c 的最大值?
且当 x= 时,
b
2a
-
y的值最大.
当a>0 ,抛物线 y = ax2+bx+c 的顶点是最低点,
即二次函数 y = ax2+bx+c 有最小值.
如何求出二次函数 y = ax2+bx+c 的最小值?
且当 x= 时,
b
2a
-
y的值最小.
利用几何图形的面积公式得到关于面积的二次函数表达式,将这个二次函数表达式进行配方(或利用顶点坐标公式),并结合实际问题的自变量的取值范围进行解答.
利用二次函数知识解面积最值问题的解题思路:
整理,得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
解: ,
∴当 时,
S 有最大值.
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
S=
60
2
-
l
l
S=
-l 2+30l
∵a=-1<0 ,
S 最大值=
l=
b
2a
-
=
-
30
2×(-1)
=15
-152+30×15
=225.
( )
例题解析
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.(1)求 y与x之间的函数关系式,并写出自变量 x 的取值范围.(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
触类旁通
D
C
B
A
25 m
xm
40
2
- x
解:
(1)
y=
40
2
- x
x
=-
2
x2
+20x
(0<x<25).
∴当 时,
y 有最大值.
∵ a=-1<0 ,
y最大值
x=
b
2a
-
40
2×(-1)
=20
=
=-
2
202
+20×20
=
200
(2)
当x是 20 m 时,绿化带的面积 S 最大.
-
学以致用
1.在半径为4cm的圆中,挖去一个边长是xcm的正方形,剩下的部分的面积为ycm2,则y与x之间的函数表达式是( ).
A.y=πx2-4 B. y=16π-x2
C.y=16-x2 D. y=x2-4π
B
2.如图,假设篱笆(虚线部分)的长度为16m,则所围成的矩形ABCD的最大面积为( ).
A.60m B. 63m2 C.64m2 D. 66m2
D
C
B
A
C
3.用长度一定的绳子围成一个矩形.如果矩形的一边长x(m)与面积y(m2)满足函数关系:
y=-x2+24x(0<x<24),则当x= m时,该矩形的面积最大,最大值为 m .
2
144
4.用长40 m的篱笆围成一个矩形菜园,设菜园的宽为xm,面积为ym2,则菜园的长为 m(用含x的整式表示),y与x的函数表达式是 .当x= 时,y取得最大值,故菜园的最大面积为 m .
(20-x)
y=-x2+20x
10
100
5.如图,要利用一面墙(墙长为50m)建羊圈,中间用墙隔开.已知计划中的建筑材料可建墙的总长度为48m,则所围成的三间羊圈的总占地面积的最大值为 m2.
A
B
C
D
50 m
144
x
(48-4x)
S=
AB·BC
=x(48-4x)
=-4x2+48x
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题? (2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
课堂小结
今天作业
课本P57页第7、8题
本节课是在学生学习完二次函数的图象和性质的知识的基础上的进一步拓展与应用.
课件说明
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
22.3实际问题与二次函数(1)
最大(或最小)面积问题
若y=ax2+bx+c(a ≠ 0),则y叫做x的二次函数;
二次函数y=ax2+bx+c的图象是一条抛物线;
当a>0时,开口向上;当a<0时,开口向下;
y=ax2+bx+c的对轴是直线x = ;
y=ax2+bx+c顶点坐标为 ( , );
y=ax2+bx+c与y轴的交点坐标为 (0,c) .
b
2a
-
b
2a
-
c
b2
4a
-
复习旧知
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
-
b
2a
-
最大值为
c
b2
4a
-
( , )
b
2a
-
x=
x
y
O
当 a> 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
b
2a
-
x=
c
b2
4a
-
最小值为
( , )
b
2a
-
求出下列抛物线最高点或最低点的坐标.
① y =-4x2+3x, ② y =3x2+x+6
解:
①
∴ 这条抛物线有最高点,
∴x =
b
2a
-
=
∴它的最高点坐标为( , ).
∵ a=-4<0 ,
3
2×(-4)
=
-
3
8
3
8
9
16
y=
=
9
16
∴ 这条抛物线开口向下,
∵ b=3 ,c=0
c
b2
4a
-
=
32
4×(-4)
0-
求出下列抛物线的有最高点或最低点吗?.
① y =-4x2+3x, ② y =3x2+x+6
解:
∴ 这条抛物线有最低点,
∴x =
b
2a
-
=
∴它的最低点坐标为( , ).
1
2×3
=
-
1
6
1
6
71
12
y=
=
71
12
∴ 这条抛物线开口向上,
∵ b=1 ,c=6,
c
b2
4a
-
=
12
4×3
6-
∵ a=3> 0 ,
-
-
②
从地面竖直向上抛出一小球,小球的高度 h
(单位:m)与小球的运动时间 t(单位:s) 之间的关系式是h= 30t -5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
x
y
o
1
2
3
4
40
20
5
6
h= 30t -5t2 (0≤t≤6).
x
y
o
1
2
3
4
40
20
5
6
h= 30t -5t2 (0≤t≤6).
从图象可以看出,这条抛物线的顶点是这个函数的图象的最高度点.
也就是说,当取顶点的横坐标时,这个函数有最大值.
从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s) 之间的关系式是
h= 30t -5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
∵ a=-5<0 ,
∵ b=30,
∴ 这个函数有最大值,
当 t=3 时,
h =30×3-5×32
=
∵当 t= 时,
b
2a
-
h有最大值.
∴
t=
b
2a
-
=
-
30
2×(-5)
=3
45
∵ a=-5<0 ,
∵ b=30,
∴ 这个函数有最大值,
当 t=3 时,
h =30×3-5×32
=
∵当 t= 时,
b
2a
-
h有最大值.
∴t=
b
2a
-
=
-
30
2×(-5)
=3
45
∴小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
当a<0 ,抛物线 y = ax2+bx+c 的顶点是最高点,
即二次函数 y = ax2+bx+c 有最大值.
如何求出二次函数 y = ax2+bx+c 的最大值?
且当 x= 时,
b
2a
-
y的值最大.
当a>0 ,抛物线 y = ax2+bx+c 的顶点是最低点,
即二次函数 y = ax2+bx+c 有最小值.
如何求出二次函数 y = ax2+bx+c 的最小值?
且当 x= 时,
b
2a
-
y的值最小.
利用几何图形的面积公式得到关于面积的二次函数表达式,将这个二次函数表达式进行配方(或利用顶点坐标公式),并结合实际问题的自变量的取值范围进行解答.
利用二次函数知识解面积最值问题的解题思路:
整理,得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
解: ,
∴当 时,
S 有最大值.
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
S=
60
2
-
l
l
S=
-l 2+30l
∵a=-1<0 ,
S 最大值=
l=
b
2a
-
=
-
30
2×(-1)
=15
-152+30×15
=225.
( )
例题解析
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.(1)求 y与x之间的函数关系式,并写出自变量 x 的取值范围.(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
触类旁通
D
C
B
A
25 m
xm
40
2
- x
解:
(1)
y=
40
2
- x
x
=-
2
x2
+20x
(0<x<25).
∴当 时,
y 有最大值.
∵ a=-1<0 ,
y最大值
x=
b
2a
-
40
2×(-1)
=20
=
=-
2
202
+20×20
=
200
(2)
当x是 20 m 时,绿化带的面积 S 最大.
-
学以致用
1.在半径为4cm的圆中,挖去一个边长是xcm的正方形,剩下的部分的面积为ycm2,则y与x之间的函数表达式是( ).
A.y=πx2-4 B. y=16π-x2
C.y=16-x2 D. y=x2-4π
B
2.如图,假设篱笆(虚线部分)的长度为16m,则所围成的矩形ABCD的最大面积为( ).
A.60m B. 63m2 C.64m2 D. 66m2
D
C
B
A
C
3.用长度一定的绳子围成一个矩形.如果矩形的一边长x(m)与面积y(m2)满足函数关系:
y=-x2+24x(0<x<24),则当x= m时,该矩形的面积最大,最大值为 m .
2
144
4.用长40 m的篱笆围成一个矩形菜园,设菜园的宽为xm,面积为ym2,则菜园的长为 m(用含x的整式表示),y与x的函数表达式是 .当x= 时,y取得最大值,故菜园的最大面积为 m .
(20-x)
y=-x2+20x
10
100
5.如图,要利用一面墙(墙长为50m)建羊圈,中间用墙隔开.已知计划中的建筑材料可建墙的总长度为48m,则所围成的三间羊圈的总占地面积的最大值为 m2.
A
B
C
D
50 m
144
x
(48-4x)
S=
AB·BC
=x(48-4x)
=-4x2+48x
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题? (2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
课堂小结
今天作业
课本P57页第7、8题
本节课是在学生学习完二次函数的图象和性质的知识的基础上的进一步拓展与应用.
课件说明
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
