18.1勾股定理 课件
图片预览

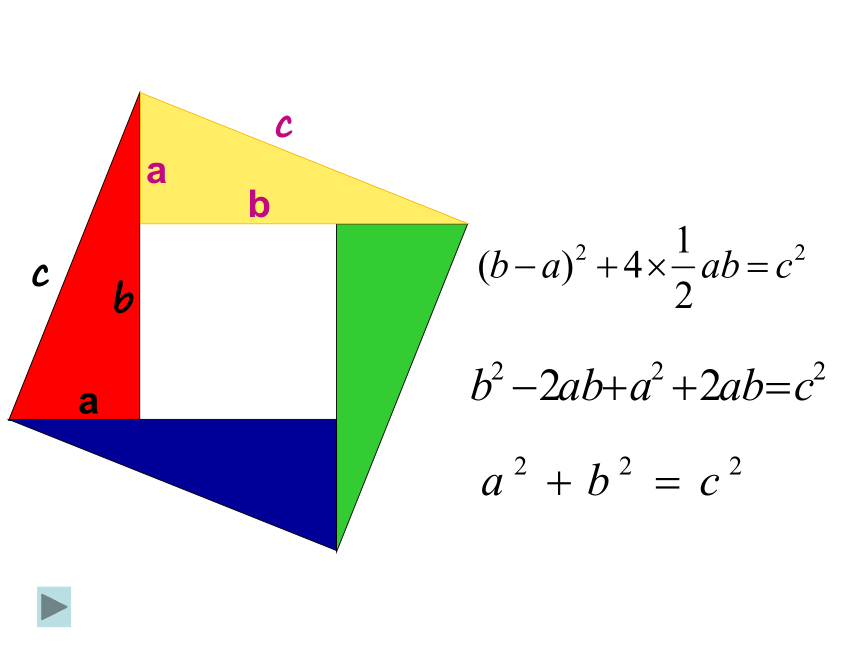
文档简介
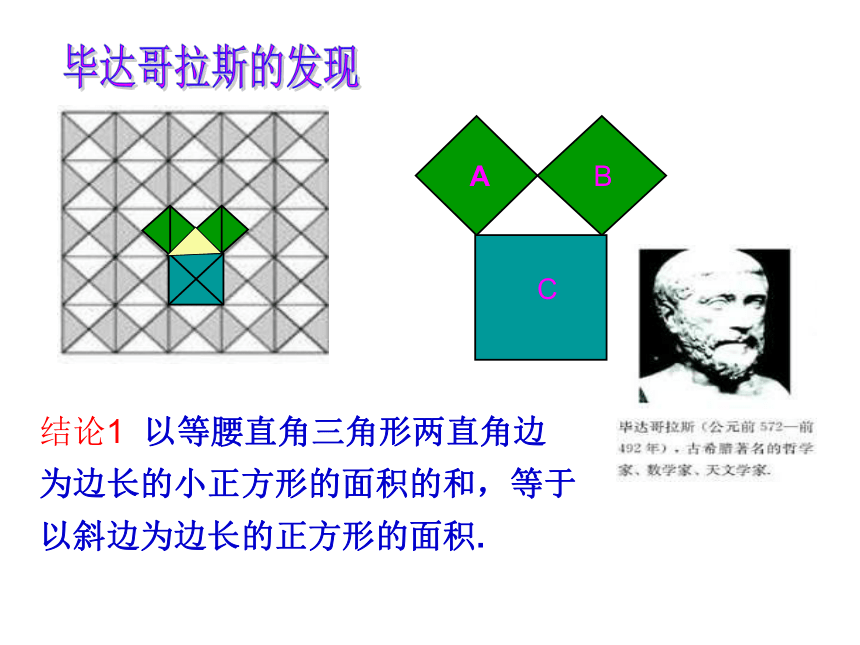
课件26张PPT。美丽的勾股树 一、情境引入 会标中央的图案是赵爽弦图,它与“勾股定理”有关,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号. 2002年世界数学家大会在我国北京召开,下图是本届数学家大会的会标:毕达哥拉斯的发现结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
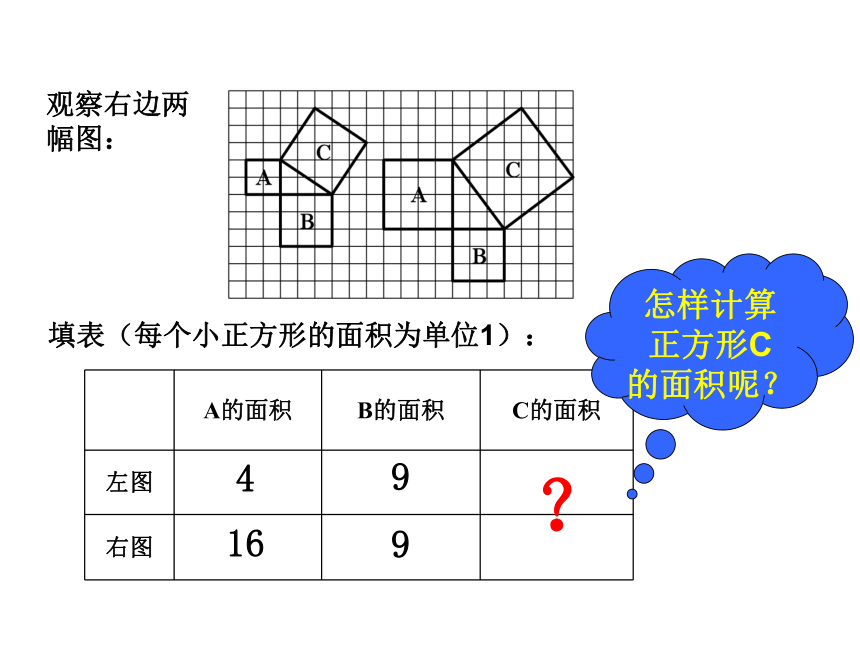
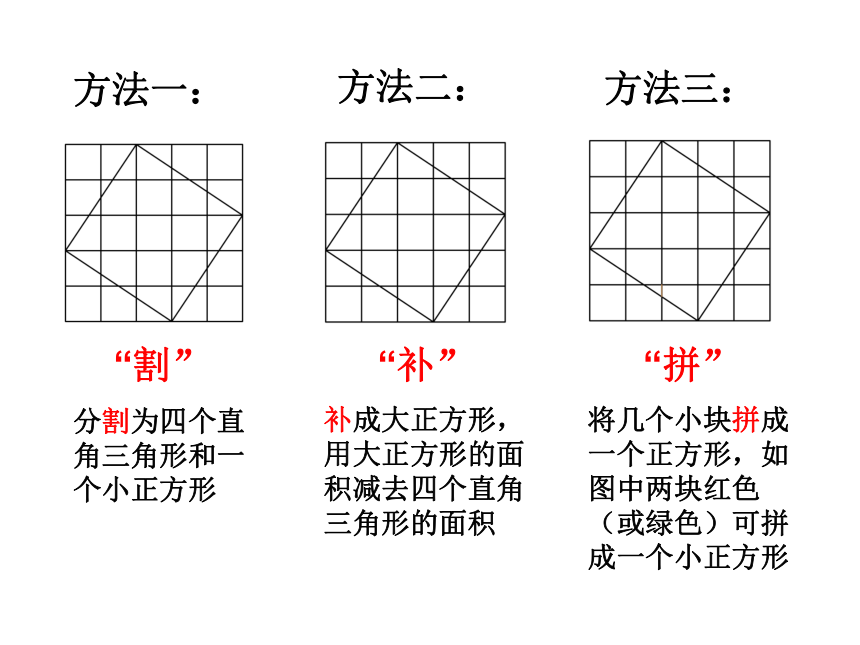
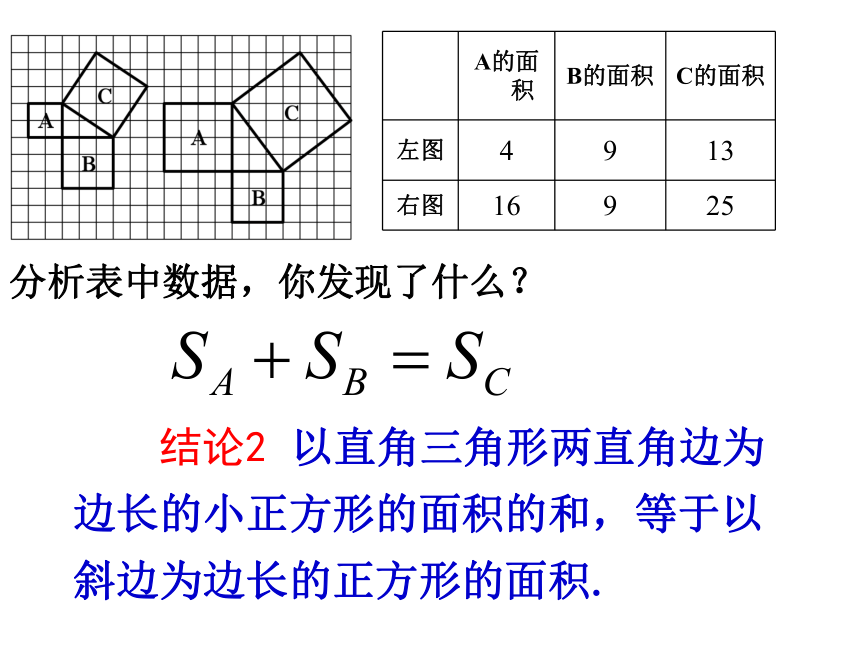
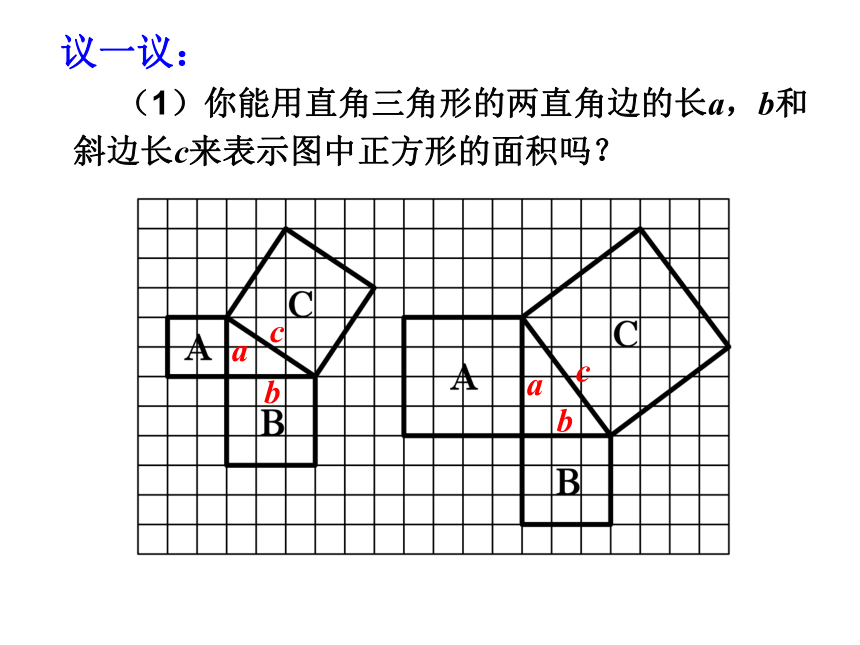
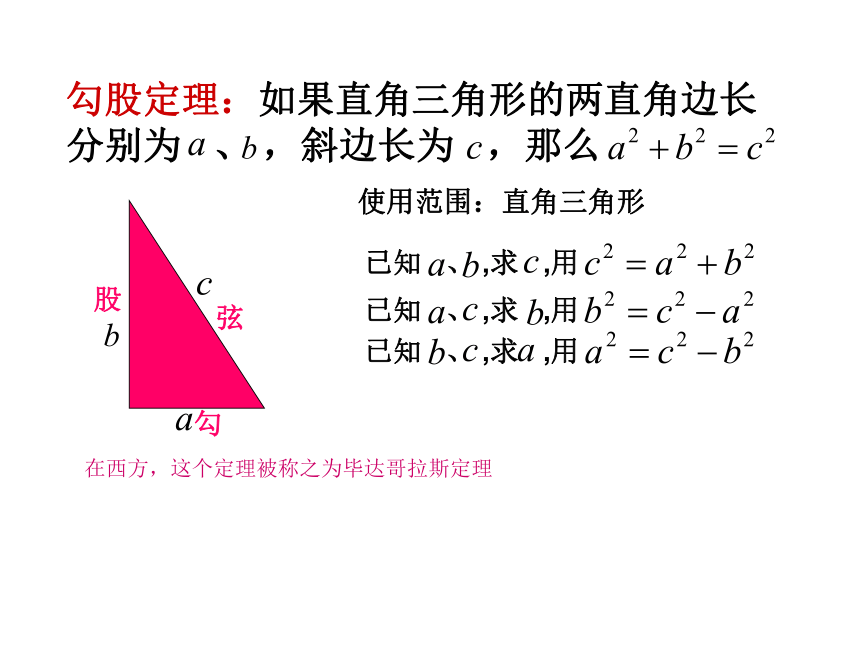
观察右边两幅图: 填表(每个小正方形的面积为单位1):4 ?怎样计算正方形C的面积呢?9 16 9 “割”“补”“拼”方法一:方法二:方法三:分割为四个直角三角形和一个小正方形补成大正方形,用大正方形的面积减去四个直角三角形的面积将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.分析表中数据,你发现了什么? 议一议: (1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗? abcabc在西方,这个定理被称之为毕达哥拉斯定理弦勾股使用范围:直角三角形abcabcbbcbc+=赵爽弦图对比两个图形,你能直接观察验证出勾股定理吗?两幅图中彩色的四个直角三角形总面积呢?提示:图中的两个大正方形面积相等吗?空白部分的面积呢?那剩余的①81144??②3352511??1045在一个直角三角形中, 两边长分别为3、4,则第三边的长为________解:若两直角边长分别为3、4,如图所示在Rt△ABC中,∠C=90°,则=32+42
=25∵AB>0,∴AB=5若一直角边长为3,斜边长为4,如图所示在Rt△ABC中,∠C=90°,则=42-32
=7C三、简单应用 例 如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树顶落在离树根24米处. 大树在折断之前高多少米?试一试:例2: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,在水池的中央有一根新生的芦苇,离河岸5尺,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。例3:在等腰三角形ABC中,已知AB=AC=5,BC=6,求△ABC的面积解:过点A作AD⊥BC于D∵AB=AC∴BD=CD在Rt△ACD中,∠ADC=90°
根据“勾股定理”得AD2=AC2 – CD2=52 -32=16∴AD=4=12即△ABC的面积为12如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°.点A处有一所中学,AP=160m,一辆拖拉机从P沿公路MN前行,假设拖拉机行驶时周围100m以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响已知拖拉机的速度为18km/h,那么学校受影响的时间为多长? 如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( ) 1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。 无字证明 abc无字证明青出青朱出入图
观察右边两幅图: 填表(每个小正方形的面积为单位1):4 ?怎样计算正方形C的面积呢?9 16 9 “割”“补”“拼”方法一:方法二:方法三:分割为四个直角三角形和一个小正方形补成大正方形,用大正方形的面积减去四个直角三角形的面积将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.分析表中数据,你发现了什么? 议一议: (1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗? abcabc在西方,这个定理被称之为毕达哥拉斯定理弦勾股使用范围:直角三角形abcabcbbcbc+=赵爽弦图对比两个图形,你能直接观察验证出勾股定理吗?两幅图中彩色的四个直角三角形总面积呢?提示:图中的两个大正方形面积相等吗?空白部分的面积呢?那剩余的①81144??②3352511??1045在一个直角三角形中, 两边长分别为3、4,则第三边的长为________解:若两直角边长分别为3、4,如图所示在Rt△ABC中,∠C=90°,则=32+42
=25∵AB>0,∴AB=5若一直角边长为3,斜边长为4,如图所示在Rt△ABC中,∠C=90°,则=42-32
=7C三、简单应用 例 如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树顶落在离树根24米处. 大树在折断之前高多少米?试一试:例2: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,在水池的中央有一根新生的芦苇,离河岸5尺,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。例3:在等腰三角形ABC中,已知AB=AC=5,BC=6,求△ABC的面积解:过点A作AD⊥BC于D∵AB=AC∴BD=CD在Rt△ACD中,∠ADC=90°
根据“勾股定理”得AD2=AC2 – CD2=52 -32=16∴AD=4=12即△ABC的面积为12如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°.点A处有一所中学,AP=160m,一辆拖拉机从P沿公路MN前行,假设拖拉机行驶时周围100m以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响已知拖拉机的速度为18km/h,那么学校受影响的时间为多长? 如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( ) 1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。 无字证明 abc无字证明青出青朱出入图
