15.2 旋转(4课时)
图片预览










文档简介
课件140张PPT。华东师大版
八年级(上)数学教学课件图形的旋转华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第1课时)钟摆(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?在平面内,将一个图形绕一个顶点沿某个方向转动一个角度,这样的图形运动称为旋转(cricumrotate),这个定点成为旋转中心,转动的角称为旋转角。旋转不改变图形的大小和形状。平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
议一议:
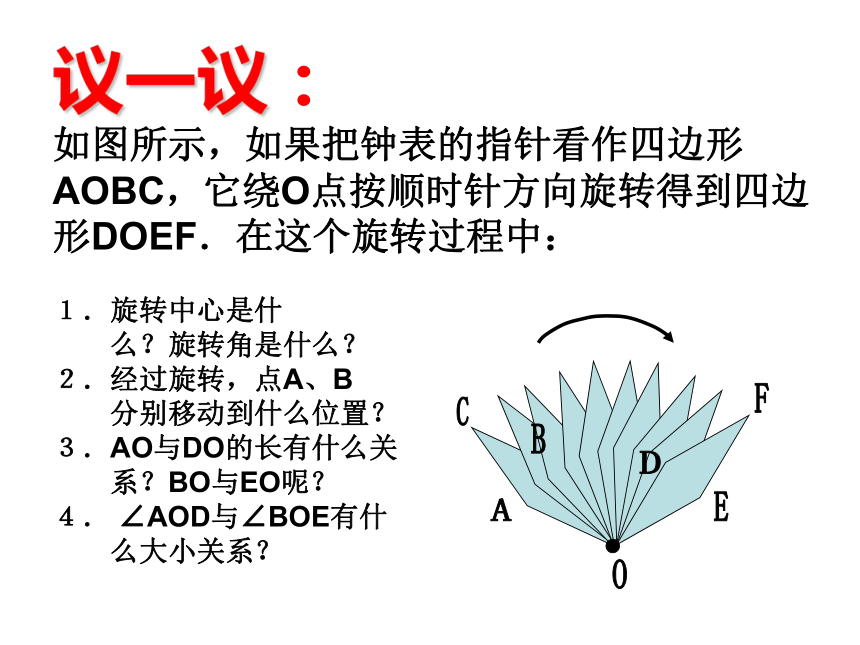
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A、B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4. ∠AOD与∠BOE有什
么大小关系?BACODEF 旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.例1 钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为 例1 △ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么(1)旋转中心是哪一点?(2)旋转角是多少?(3)连接PP’后,△BPP’是什么三角形?解 (1)旋转中心是点B。(2) 旋转角等于60°。(3)因为BP′=BP,
∠ PBP′=∠ABC= 60°,
所以△BPP’是等边三角形(有一个角
等于60°的等腰三角形是等边三角形)。巩固练习:1. 四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?(2)旋转角是多少?(3)连接EF后,△DEF是什么三角形?探究:如果等边△ABD旋转后与等边△BCD重合,那么在图形所在的平面内可作为旋转中心的点有几个?试一试:某个学生为学校设计了一个直角三角形的绿化带,有一块是正方形草坪和两块直角三角形的花坛组成,现在只知道两个直角三角形的两条斜边长分别为3米和6米,你能求出花坛的面积是多少吗?3米6米随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH
试设计一个旋转45 °后与自身重合的图形。旋转的特征华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第2课时)探 索 观察下图,你能发现有哪些线段相等?有哪些角相等? 在图中,线段OA、 OB都是绕点O逆时针旋转45°到对应线段OA? 、 OB? ,而且45°A? B? 我们可以看到,OA=OA? , OB=OB? , AB=A? B? ;∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? . 在图中,旋转中心是点O,点A、 B、 C都是绕点O逆时针旋转60°到对应点A? 、 B? 、 C? ,而且 再观察下图,你能发现有哪些线段相等?有哪些角相等?O60°OA= , OB= , OC= ;AB= , BC= , CA= ;∠CAB= , ∠ABC= , ∠BCA= .旋转的基本性质(1)旋转不改变图形的形状和大小.
(2)图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度.
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
(5)对应线段相等,对应角相等.C? ABCA? B? A? B? C? 如图,在纸上画△ABC和过点P的两条直线PQ、PR.画出△ABC关于PQ对称的△A? B? C? ,再画出△A? B? C?关于PR对称的△A? B? C? .
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?结论: 两次翻折(对称轴相交)相当于一次旋转.A? B? C? 例1 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.(1) 作OA? ?OA,取OA? =OA,OB? = OB;(2) 连接OC;(3) 作OC? ?OC,取OC? =OC;(4) 连接A? C? 、B? C?.┓┓ 即可作出“小旗子”按要求旋转后的图案.解:例2 已知等边?ABC,作出它绕点B按逆时针方向旋转120°后的三角形.A? C? ABC解:(1)延长CB到点A? ,(2)分别以点A?、B为圆心,(3) 连接A? C? 、C? B.则?A? BC? 就是满足条件的三角形.使A? B=A B.以A?B长为半径画弧,在直线A?C的上侧交于点C?.例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点?(2)旋转了多少度?(3)线段AF与BE的位置关系如何?如何找旋转中心呢?旋转中心在对应点连线的垂直平分线上,你知道为什么吗?怎样画一个图形关于一个点旋转后的图形?思考:如何来确定旋转中心?主要是画图形上的几个点旋转后的对应点.用对称点连线的中垂线来确定.1.如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心( ),旋转角是( ).(2)经过旋转,点A、B分别移到了( ).(3)若AO=3cm,则CO=( ).(4) 若∠AOC=60°,∠AOD=20°,则∠BOD=( ),
∠DOC=( ).练习2. 如图,P为正方形ABCD中一点,把三角形BPC旋转到三角形DQC,请说出旋转中心,对应点、对应线段、对应角、旋转角以及旋转角度是多少?PQ若连接PQ,则△PCQ是什么三角形?3.如图所示,在△ABC中,M是BC边上的一点, △ABC经过旋转后到达△AMN的位置,∠BAM=40°,求:(1)旋转中心是哪一点?(2)旋转的角度是多少?(3)若H是AB边上的一点,且CH⊥AB,则点H旋转到了什么位置?(4)若将题中的∠BAM=40°改为∠ABC=70°,问题(2)的结论是什么?KHMN40°┓┓4. 如图,四边形ABCD与四边形EFGO都是边长相等的的正方形,对角线AC与BD交于点O,那么正方形EFGO绕点O无论怎样转动,请你猜想,两个正方形重叠部分的面积会是一个正方形面积的多少?你能否用旋转有关知识说明理由.ABCDOEFGKH利用旋转来解决数学问题 利用图形的旋转可以使分散的条件与结论相对地集中,以便发现条件与结论之间的关系,从而获得问题解决的思路与途径。5.在正方形ABCD中, ∠1=∠2 =30°.试把ΔADE绕点A顺时针旋转90°,观察整个图形中角与角之间,线段与线段之间,存在哪些相等关系?探索DE,BF,AF之间的关系.(1)已知△ABC和点O,画出△ABC绕着点O逆时针旋转80°后所得的△A? B? C? ;
(2)已知△ABC和直线MN,画出△ABC关于直线MN对称的△A? B? C?. 课外练习:ABCMN(1)(2) 如图,正方形ABCD的边长为1, AB、AD上各有一点P、Q,如果三角形APQ的周长为2,求∠PCQ。提高题如图,把ΔDQC逆时针方向旋转90°到ΔBEC
则DQ=BE,CQ=CE。有QP=2-AQ-AP,
EP=BP+BE=BP+DQ= (1-AP) + (1-AQ) =QP
所以ΔQCP≌ΔECP(SSS)所以∠PCQ= ∠PCE=45 °*解决问题A?B?如图,河两边有A、B两个村庄,现准备建一座桥,桥必须与河岸垂直,问桥应建在何处才能使由甲到乙的路程最短?请作出图形,并说说理由.CED华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第3课时)旋转对称图形例一例二图形欣赏結束这个是轴对称图形,它也是旋转对称图形吗?旋转180度,重复第一次。旋转360度,重复第二次。旋转360度,共重复二次,因此它也是旋转对称图形。这是旋转对称图形吗?旋转一周重复多少次?旋转90度,重复第一次。旋转180度,重合第二次。旋转270度,重合第三次。旋转360度,重合第四次。旋转360度,共重合四次,因此是旋转对称图形。旋转对称图形欣赏旋转一周重合两次.旋转一周重合两次旋转一周重合两次旋转一周重合两次旋转一周重合两次旋转一周重合三次旋转一周重合三次旋转一周重合四次旋转一周重合四次旋转一周重合五次旋转一周重合八次旋转一周重合八次旋转一周重合八次旋转一周重合无数次华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第4课时)课堂练习复习提问:1.什么叫平移?有何性质?2.什么叫旋转?有何性质?在平面内,将一个图形绕一个定点沿顺时针或逆时针转动一定的角度。这个定点称为旋转中心转动的角度称为旋转角。图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.任意一对对应点与旋转中心的连线所成的角度都是旋转角.对应点到旋转中心的距离相等.550600C画出所给图形绕点o顺时针旋转90度后的图案O例1 △ ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B的对应点的位置,以及旋转后的三角形。BACED议一议你还有其他方法作出 DEC吗?DBAC..E△在旋转过程中,确定一个三角形旋转后的位置,除需要此三角形原来位置外,还需要什么条件?1、三角形原来的位置2、旋转中心3、旋转角练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.
等边△ABC的边长为1,∠BDC=120°,BD=CD,
∠MDN=60°
求△AMN的周长.
八年级(上)数学教学课件图形的旋转华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第1课时)钟摆(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?在平面内,将一个图形绕一个顶点沿某个方向转动一个角度,这样的图形运动称为旋转(cricumrotate),这个定点成为旋转中心,转动的角称为旋转角。旋转不改变图形的大小和形状。平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A、B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4. ∠AOD与∠BOE有什
么大小关系?BACODEF 旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.例1 钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为 例1 △ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么(1)旋转中心是哪一点?(2)旋转角是多少?(3)连接PP’后,△BPP’是什么三角形?解 (1)旋转中心是点B。(2) 旋转角等于60°。(3)因为BP′=BP,
∠ PBP′=∠ABC= 60°,
所以△BPP’是等边三角形(有一个角
等于60°的等腰三角形是等边三角形)。巩固练习:1. 四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?(2)旋转角是多少?(3)连接EF后,△DEF是什么三角形?探究:如果等边△ABD旋转后与等边△BCD重合,那么在图形所在的平面内可作为旋转中心的点有几个?试一试:某个学生为学校设计了一个直角三角形的绿化带,有一块是正方形草坪和两块直角三角形的花坛组成,现在只知道两个直角三角形的两条斜边长分别为3米和6米,你能求出花坛的面积是多少吗?3米6米随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH
试设计一个旋转45 °后与自身重合的图形。旋转的特征华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第2课时)探 索 观察下图,你能发现有哪些线段相等?有哪些角相等? 在图中,线段OA、 OB都是绕点O逆时针旋转45°到对应线段OA? 、 OB? ,而且45°A? B? 我们可以看到,OA=OA? , OB=OB? , AB=A? B? ;∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? . 在图中,旋转中心是点O,点A、 B、 C都是绕点O逆时针旋转60°到对应点A? 、 B? 、 C? ,而且 再观察下图,你能发现有哪些线段相等?有哪些角相等?O60°OA= , OB= , OC= ;AB= , BC= , CA= ;∠CAB= , ∠ABC= , ∠BCA= .旋转的基本性质(1)旋转不改变图形的形状和大小.
(2)图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度.
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
(5)对应线段相等,对应角相等.C? ABCA? B? A? B? C? 如图,在纸上画△ABC和过点P的两条直线PQ、PR.画出△ABC关于PQ对称的△A? B? C? ,再画出△A? B? C?关于PR对称的△A? B? C? .
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?结论: 两次翻折(对称轴相交)相当于一次旋转.A? B? C? 例1 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.(1) 作OA? ?OA,取OA? =OA,OB? = OB;(2) 连接OC;(3) 作OC? ?OC,取OC? =OC;(4) 连接A? C? 、B? C?.┓┓ 即可作出“小旗子”按要求旋转后的图案.解:例2 已知等边?ABC,作出它绕点B按逆时针方向旋转120°后的三角形.A? C? ABC解:(1)延长CB到点A? ,(2)分别以点A?、B为圆心,(3) 连接A? C? 、C? B.则?A? BC? 就是满足条件的三角形.使A? B=A B.以A?B长为半径画弧,在直线A?C的上侧交于点C?.例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点?(2)旋转了多少度?(3)线段AF与BE的位置关系如何?如何找旋转中心呢?旋转中心在对应点连线的垂直平分线上,你知道为什么吗?怎样画一个图形关于一个点旋转后的图形?思考:如何来确定旋转中心?主要是画图形上的几个点旋转后的对应点.用对称点连线的中垂线来确定.1.如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心( ),旋转角是( ).(2)经过旋转,点A、B分别移到了( ).(3)若AO=3cm,则CO=( ).(4) 若∠AOC=60°,∠AOD=20°,则∠BOD=( ),
∠DOC=( ).练习2. 如图,P为正方形ABCD中一点,把三角形BPC旋转到三角形DQC,请说出旋转中心,对应点、对应线段、对应角、旋转角以及旋转角度是多少?PQ若连接PQ,则△PCQ是什么三角形?3.如图所示,在△ABC中,M是BC边上的一点, △ABC经过旋转后到达△AMN的位置,∠BAM=40°,求:(1)旋转中心是哪一点?(2)旋转的角度是多少?(3)若H是AB边上的一点,且CH⊥AB,则点H旋转到了什么位置?(4)若将题中的∠BAM=40°改为∠ABC=70°,问题(2)的结论是什么?KHMN40°┓┓4. 如图,四边形ABCD与四边形EFGO都是边长相等的的正方形,对角线AC与BD交于点O,那么正方形EFGO绕点O无论怎样转动,请你猜想,两个正方形重叠部分的面积会是一个正方形面积的多少?你能否用旋转有关知识说明理由.ABCDOEFGKH利用旋转来解决数学问题 利用图形的旋转可以使分散的条件与结论相对地集中,以便发现条件与结论之间的关系,从而获得问题解决的思路与途径。5.在正方形ABCD中, ∠1=∠2 =30°.试把ΔADE绕点A顺时针旋转90°,观察整个图形中角与角之间,线段与线段之间,存在哪些相等关系?探索DE,BF,AF之间的关系.(1)已知△ABC和点O,画出△ABC绕着点O逆时针旋转80°后所得的△A? B? C? ;
(2)已知△ABC和直线MN,画出△ABC关于直线MN对称的△A? B? C?. 课外练习:ABCMN(1)(2) 如图,正方形ABCD的边长为1, AB、AD上各有一点P、Q,如果三角形APQ的周长为2,求∠PCQ。提高题如图,把ΔDQC逆时针方向旋转90°到ΔBEC
则DQ=BE,CQ=CE。有QP=2-AQ-AP,
EP=BP+BE=BP+DQ= (1-AP) + (1-AQ) =QP
所以ΔQCP≌ΔECP(SSS)所以∠PCQ= ∠PCE=45 °*解决问题A?B?如图,河两边有A、B两个村庄,现准备建一座桥,桥必须与河岸垂直,问桥应建在何处才能使由甲到乙的路程最短?请作出图形,并说说理由.CED华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第3课时)旋转对称图形例一例二图形欣赏結束这个是轴对称图形,它也是旋转对称图形吗?旋转180度,重复第一次。旋转360度,重复第二次。旋转360度,共重复二次,因此它也是旋转对称图形。这是旋转对称图形吗?旋转一周重复多少次?旋转90度,重复第一次。旋转180度,重合第二次。旋转270度,重合第三次。旋转360度,重合第四次。旋转360度,共重合四次,因此是旋转对称图形。旋转对称图形欣赏旋转一周重合两次.旋转一周重合两次旋转一周重合两次旋转一周重合两次旋转一周重合两次旋转一周重合三次旋转一周重合三次旋转一周重合四次旋转一周重合四次旋转一周重合五次旋转一周重合八次旋转一周重合八次旋转一周重合八次旋转一周重合无数次华东师大版八年级(上册)第15章 平移与旋转15.2 旋转(第4课时)课堂练习复习提问:1.什么叫平移?有何性质?2.什么叫旋转?有何性质?在平面内,将一个图形绕一个定点沿顺时针或逆时针转动一定的角度。这个定点称为旋转中心转动的角度称为旋转角。图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.任意一对对应点与旋转中心的连线所成的角度都是旋转角.对应点到旋转中心的距离相等.550600C画出所给图形绕点o顺时针旋转90度后的图案O例1 △ ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B的对应点的位置,以及旋转后的三角形。BACED议一议你还有其他方法作出 DEC吗?DBAC..E△在旋转过程中,确定一个三角形旋转后的位置,除需要此三角形原来位置外,还需要什么条件?1、三角形原来的位置2、旋转中心3、旋转角练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.
等边△ABC的边长为1,∠BDC=120°,BD=CD,
∠MDN=60°
求△AMN的周长.
