2021-2022学年人教版数学八年级下册19.2.1正比例函数(第2课时)课件 (共23张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册19.2.1正比例函数(第2课时)课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 770.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 21:51:51 | ||
图片预览







文档简介
(共23张PPT)
19.2.1
正比例函数(2)
温故知新
1. 什么是正比例函数?
一般地,形如 y = kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
温故知新
2. 下列函数中哪些是正比例函数?
① ②
③ ④
⑤ ⑥
⑦ ⑧
是
是
是
是
是
否
否
是
温故知新
3. 描点法画函数图象的一般步骤是什么?
情景引入
画出下列函数的图象
(1)
(2)
(3)
(4)
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
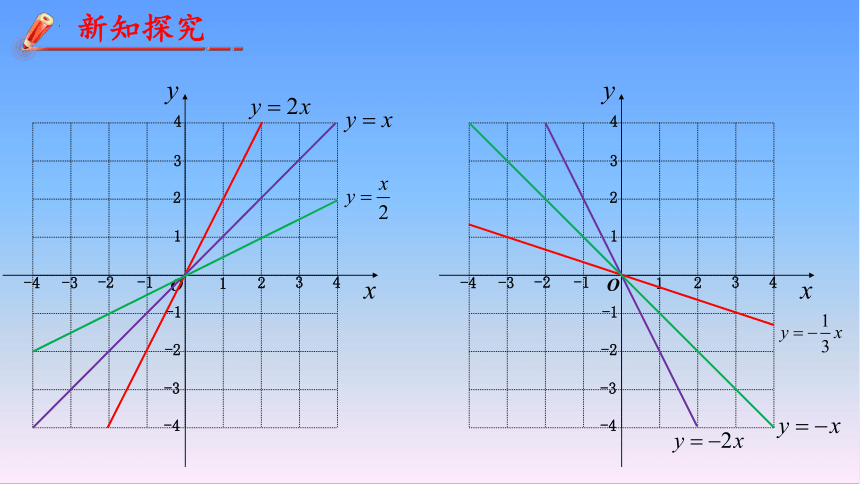
观察与发现
对于正比例函数的图像:
①它的图象是什么形状?
②图象必过什么特殊的点?
③图象落在哪些象限?
④图象有怎样的变化趋势?
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
新知探究
共同点:都是经过原点的直线
一般地,正比例函数 y = kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线 y = kx.
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
当k>0时,直线y=kx经过第一、第三象限,从左向右上升,即随着x的增大y也增大,也可描述为y随着x的增大而增大.
不同点:
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小,也可描述为y随着x的增大而减小.
不同点:
新知探究
正比例函数的性质:
当k>0时,直线y=kx经过第一、第三象限,从左向右上升,即随着x的增大y也增大,也可描述为y随着x的增大而增大.
当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小,也可描述为y随着x的增大而减小.
(“正增负减”)
牛刀初试
判断下列正比例函数的图象经过第几象限?有什么变化趋势?
① ②
③ ④
新知探究
一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图象.
两点法
趁热打铁
用两点法画出下列正比例函数的图象.
①
②
典例解析
已知正比例函数 .
(1)m为何值时,函数图象经过第一、第三象限?
(2)m为何值时,y随x的增大而减小?
(3)m为何值时,点(1,3)在该函数图象上?
2.已知 ab < 0,则函数 的图象经过
象限.
随堂演练
1.正比例函数的解析式是 ,
它的图象必过 .
原点
y = kx(k≠0)
第二、第四
随堂演练
3.在下列各图象中,表示函数
的图象的是( ).
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
C
已知正比例函数 的图象经过点(3,-6)
(1)若点(-2,m)在函数 的图象上,求m.
(2)图象上有两点A ,B ,如果 ,试判断 , 的大小.
思维拓展
聚沙成塔
正比例函数的概念
描点法
归纳总结
两点法
探究
经过象限和变化趋势
一条过原点
的直线
相同点
不同点
正比例函数的图象
正比例函数的性质
k > 0 k < 0
经过象限 第一、第三象限 第二、第四象限
变化趋势 上升 下降
课后巩固
作业精选与设计
必做基础题:课本89页 练习题
必做提升题:配套练习1,2,3,4,5,6
自选拔高题:
①配套练习8,9,10
②配套练习7,11,13
③配套练习12,14
下课!
19.2.1
正比例函数(2)
温故知新
1. 什么是正比例函数?
一般地,形如 y = kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
温故知新
2. 下列函数中哪些是正比例函数?
① ②
③ ④
⑤ ⑥
⑦ ⑧
是
是
是
是
是
否
否
是
温故知新
3. 描点法画函数图象的一般步骤是什么?
情景引入
画出下列函数的图象
(1)
(2)
(3)
(4)
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
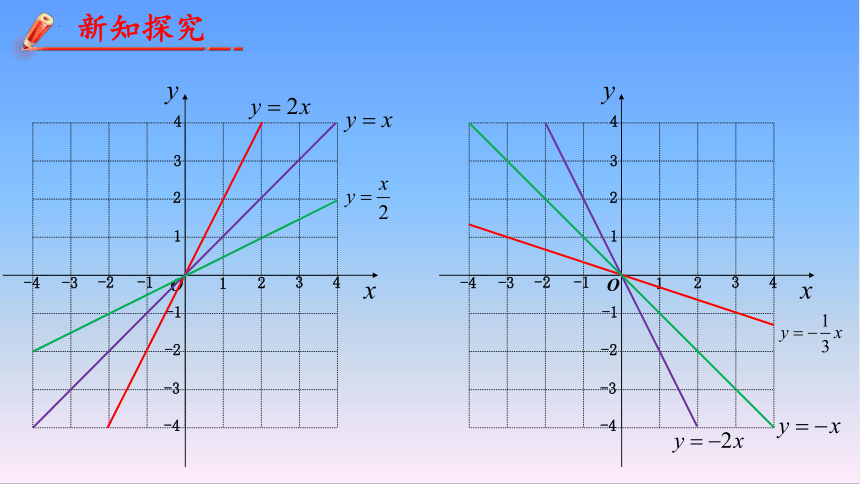
观察与发现
对于正比例函数的图像:
①它的图象是什么形状?
②图象必过什么特殊的点?
③图象落在哪些象限?
④图象有怎样的变化趋势?
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
新知探究
共同点:都是经过原点的直线
一般地,正比例函数 y = kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线 y = kx.
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
当k>0时,直线y=kx经过第一、第三象限,从左向右上升,即随着x的增大y也增大,也可描述为y随着x的增大而增大.
不同点:
新知探究
O
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小,也可描述为y随着x的增大而减小.
不同点:
新知探究
正比例函数的性质:
当k>0时,直线y=kx经过第一、第三象限,从左向右上升,即随着x的增大y也增大,也可描述为y随着x的增大而增大.
当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小,也可描述为y随着x的增大而减小.
(“正增负减”)
牛刀初试
判断下列正比例函数的图象经过第几象限?有什么变化趋势?
① ②
③ ④
新知探究
一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图象.
两点法
趁热打铁
用两点法画出下列正比例函数的图象.
①
②
典例解析
已知正比例函数 .
(1)m为何值时,函数图象经过第一、第三象限?
(2)m为何值时,y随x的增大而减小?
(3)m为何值时,点(1,3)在该函数图象上?
2.已知 ab < 0,则函数 的图象经过
象限.
随堂演练
1.正比例函数的解析式是 ,
它的图象必过 .
原点
y = kx(k≠0)
第二、第四
随堂演练
3.在下列各图象中,表示函数
的图象的是( ).
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
C
已知正比例函数 的图象经过点(3,-6)
(1)若点(-2,m)在函数 的图象上,求m.
(2)图象上有两点A ,B ,如果 ,试判断 , 的大小.
思维拓展
聚沙成塔
正比例函数的概念
描点法
归纳总结
两点法
探究
经过象限和变化趋势
一条过原点
的直线
相同点
不同点
正比例函数的图象
正比例函数的性质
k > 0 k < 0
经过象限 第一、第三象限 第二、第四象限
变化趋势 上升 下降
课后巩固
作业精选与设计
必做基础题:课本89页 练习题
必做提升题:配套练习1,2,3,4,5,6
自选拔高题:
①配套练习8,9,10
②配套练习7,11,13
③配套练习12,14
下课!
