八年级数学期末复习讲义(无答案)
图片预览

文档简介
初 二 数 学
期 末 复 习
一、例题精讲:
1、如图,直线的函数表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的函数表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得
与的面积相等,请直接写出点的坐标.
2、如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)请判断EO与FO的数量关系并且说明理由。
(2)当点O运动到何处时,四边形AECF是矩形?
请说明理由.
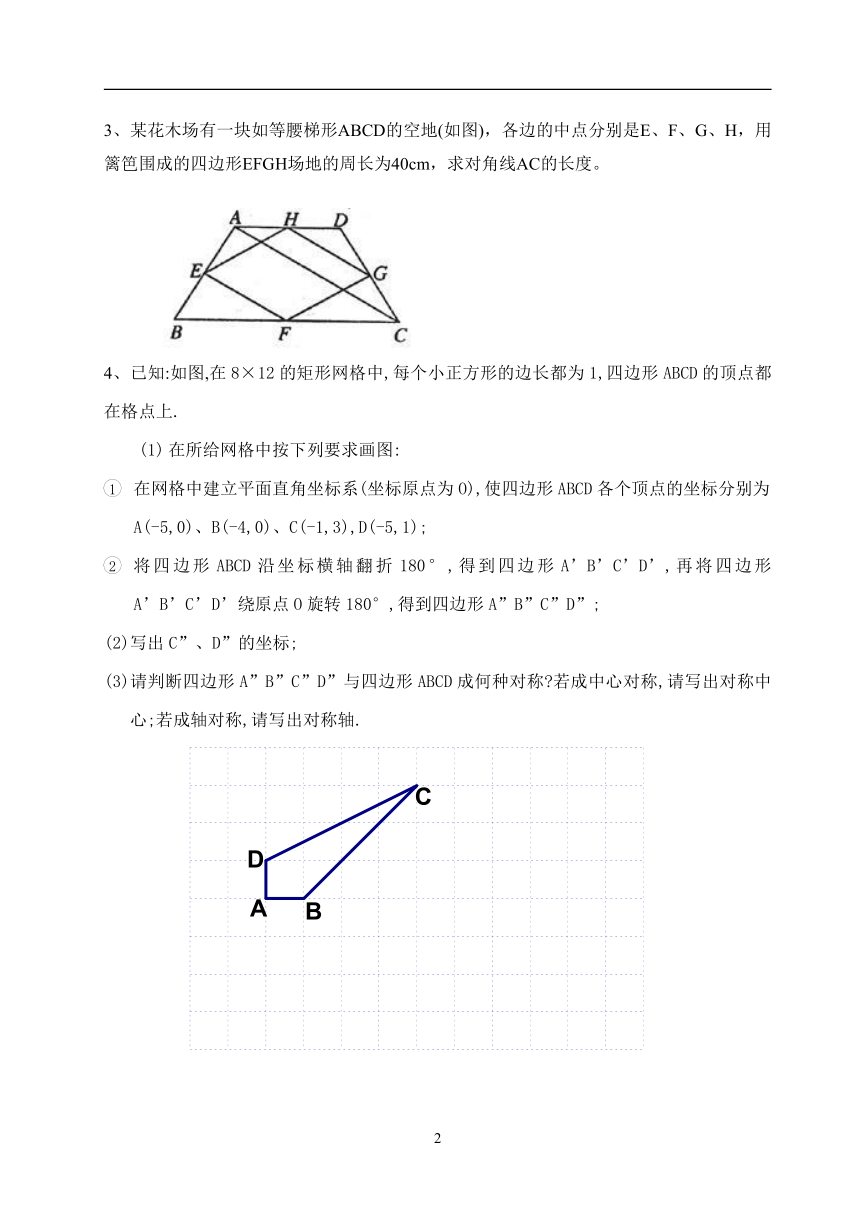
3、某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为40cm,求对角线AC的长度。
4、已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
(1) 在所给网格中按下列要求画图:
1 在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);
2 将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;
(2)写出C”、D”的坐标;
(3)请判断四边形A”B”C”D”与四边形ABCD成何种对称 若成中心对称,请写出对称中心;若成轴对称,请写出对称轴.
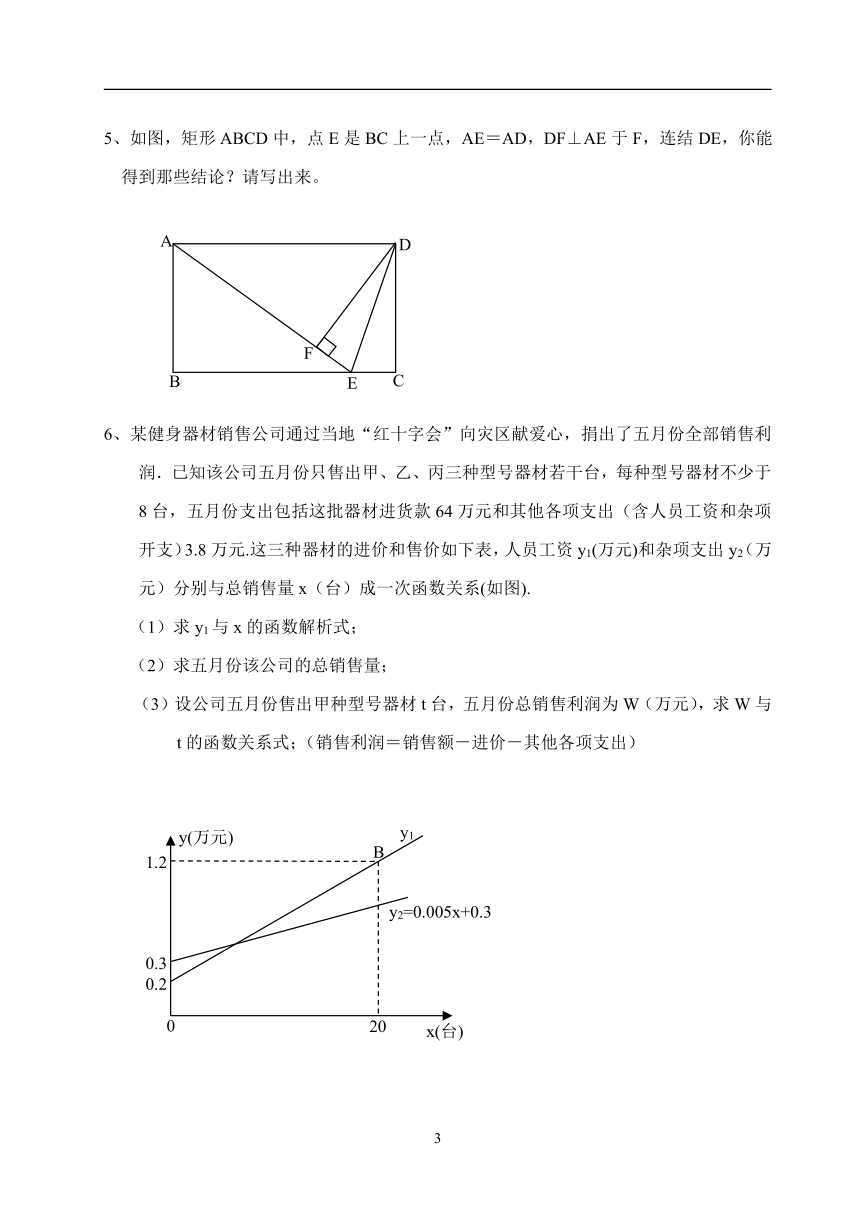
5、如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F,连结DE,你能得到那些结论?请写出来。
6、某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
二、同步练习:
1、一组数据4、5、x、7的平均数是5,则x =
2、经过点A(3,9)的正比例函数解析式是_____ _____;
3、函数中y随x的增大而增大,则k_____0(填>,=或<)
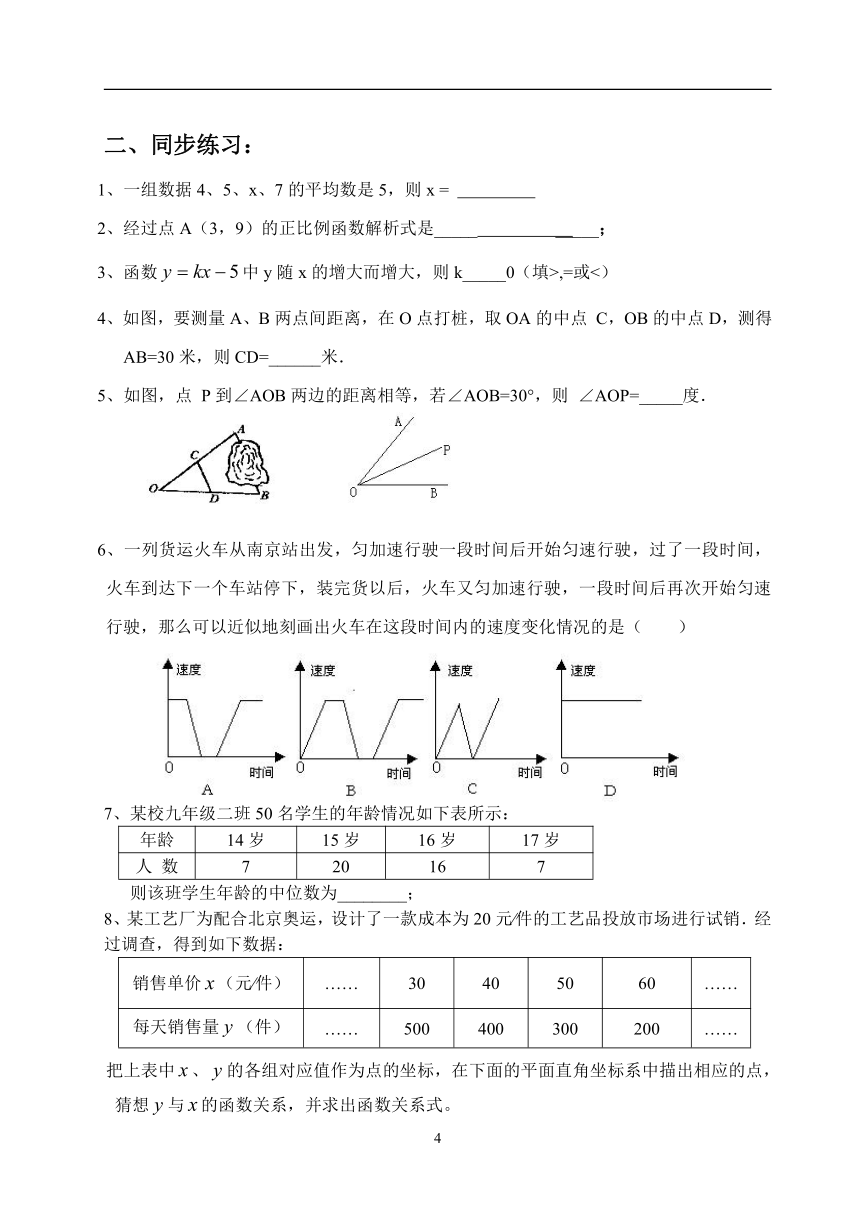
4、如图,要测量A、B两点间距离,在O点打桩,取OA的中点 C,OB的中点D,测得AB=30米,则CD=______米.
5、如图,点 P到∠AOB两边的距离相等,若∠AOB=30°,则 ∠AOP=_____度.
6、一列货运火车从南京站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,装完货以后,火车又匀加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是( )
7、某校九年级二班50名学生的年龄情况如下表所示:
年龄 14岁 15岁 16岁 17岁
人 数 7 20 16 7
则该班学生年龄的中位数为________;
8、某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价(元∕件) …… 30 40 50 60 ……
每天销售量(件) …… 500 400 300 200 ……
把上表中、的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想与的函数关系,并求出函数关系式。
巩固练习:
1.下列图案既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.立方根等于它本身的数是( )
A.1,0 B.±1 C.0,—1 D.±1,0
3.10名初中毕业生的中考体育考试成绩如下:25、 26、 26 、26、 26、 27、 28、 29、 29、 30 ,这些成绩的中位数是( )
A.25 B.26
C.26.5 D.30
4. 如图, 点M(-3,4)到原点的距离是( )
A.3 B.4
C.5 D.7
5.已知1、2、3、的平均数是8,那么的值是 ( )
A.14 B.22 C.32 D.42
6.在直角坐标系中,既是正比例函数,又是的值随值的增大而减小的图像是( )
A. B. C. D.
7.已知正比例函数y=kx中若y随x的增大而减小,则k的取值范围是( )
A.k<0 B.k>0 C.k=0 D.k<1
8.如图,已知菱形ABCD的周长为8,∠ABC=60 ,则菱形的面积为 ( )
A. B.
C. D.
9. 25的算术平方根是 ,平方根是 .
10.已知梯形的中位线长为6cm,高为4cm,则此梯形的面积为_________cm2.
11.直线与的位置关系为 .
12.饮料每箱6瓶,售价55元。买的总价y(元)与所买瓶数x之间的函数关系式是 .
13.如图,用(0,0)表示M点的位置, 用(2,3)表示O点的位置,
则N点的位置可以用 表示.
14.点A(-3,4)关于原点对称的点的坐标为 .
15.对于函数,y的值随x值的增大而 .
16.已知二元一次方程中,若x=3时,y= ;若y=1时,则x= .
17.一个汽车牌在水中的倒影为 ,则该车牌照号码为 .
18.如下图是一个简单的数值运算程序,当输入x的值为-1时,输出的数值为______.
19.已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.
(1)△BCE与哪一个三角形全等?试说明你的理由;
(2)若AB⊥BC 且BC=4,AB=6,求EF的长.
20.一次函数y=kx+4的图象经过点(-3,-2),则
(1)求这个函数表达式;
(2)判断(-5,3)是否在此函数的图象上;
(3)建立适当坐标系,画出该函数的图象.
21.如图,已知两直线l1和l2相交于点A(4,3),且OA=OB,请分别求出两条直线对应的函数关系式.
22.如图,在□ABCD中,E、F是对角线AC上的点,且AE=CF,试说明四边形BFDE是平行四边形.
23. 已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个
△DEC,且使DE∥AC,CE∥BD,试判断四边形DECP的形状并且说明理由。
24.抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库。已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨。从甲、乙两库到A、B两库的路程和运费如下表(表中“元/吨·千米”表示每吨粮食运送1千米所需人民币)
(1)若甲库运往A库粮食吨,请写出将粮食运往A、B两库的总运费(元)与(吨)的函数关系式
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
A
C
B
D
FFfFFFF
E
输出
-2
×(-3)
输入x
(第15题图)
N
M
O
O
y
x
O
x
y
O
x
y
O
y
x
(第4题)图)
0
-3
4
M
x
y
E
F
D
C
B
A
(4,0)
A
C
B
3
O
D
y
x
l2
l1
y(万元)
x(台)
y2=0.005x+0.3
y1
B
1.2
0.3
0.2
20
0
PAGE
1
期 末 复 习
一、例题精讲:
1、如图,直线的函数表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的函数表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得
与的面积相等,请直接写出点的坐标.
2、如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)请判断EO与FO的数量关系并且说明理由。
(2)当点O运动到何处时,四边形AECF是矩形?
请说明理由.
3、某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为40cm,求对角线AC的长度。
4、已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
(1) 在所给网格中按下列要求画图:
1 在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);
2 将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;
(2)写出C”、D”的坐标;
(3)请判断四边形A”B”C”D”与四边形ABCD成何种对称 若成中心对称,请写出对称中心;若成轴对称,请写出对称轴.
5、如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F,连结DE,你能得到那些结论?请写出来。
6、某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
二、同步练习:
1、一组数据4、5、x、7的平均数是5,则x =
2、经过点A(3,9)的正比例函数解析式是_____ _____;
3、函数中y随x的增大而增大,则k_____0(填>,=或<)
4、如图,要测量A、B两点间距离,在O点打桩,取OA的中点 C,OB的中点D,测得AB=30米,则CD=______米.
5、如图,点 P到∠AOB两边的距离相等,若∠AOB=30°,则 ∠AOP=_____度.
6、一列货运火车从南京站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,装完货以后,火车又匀加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是( )
7、某校九年级二班50名学生的年龄情况如下表所示:
年龄 14岁 15岁 16岁 17岁
人 数 7 20 16 7
则该班学生年龄的中位数为________;
8、某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价(元∕件) …… 30 40 50 60 ……
每天销售量(件) …… 500 400 300 200 ……
把上表中、的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想与的函数关系,并求出函数关系式。
巩固练习:
1.下列图案既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.立方根等于它本身的数是( )
A.1,0 B.±1 C.0,—1 D.±1,0
3.10名初中毕业生的中考体育考试成绩如下:25、 26、 26 、26、 26、 27、 28、 29、 29、 30 ,这些成绩的中位数是( )
A.25 B.26
C.26.5 D.30
4. 如图, 点M(-3,4)到原点的距离是( )
A.3 B.4
C.5 D.7
5.已知1、2、3、的平均数是8,那么的值是 ( )
A.14 B.22 C.32 D.42
6.在直角坐标系中,既是正比例函数,又是的值随值的增大而减小的图像是( )
A. B. C. D.
7.已知正比例函数y=kx中若y随x的增大而减小,则k的取值范围是( )
A.k<0 B.k>0 C.k=0 D.k<1
8.如图,已知菱形ABCD的周长为8,∠ABC=60 ,则菱形的面积为 ( )
A. B.
C. D.
9. 25的算术平方根是 ,平方根是 .
10.已知梯形的中位线长为6cm,高为4cm,则此梯形的面积为_________cm2.
11.直线与的位置关系为 .
12.饮料每箱6瓶,售价55元。买的总价y(元)与所买瓶数x之间的函数关系式是 .
13.如图,用(0,0)表示M点的位置, 用(2,3)表示O点的位置,
则N点的位置可以用 表示.
14.点A(-3,4)关于原点对称的点的坐标为 .
15.对于函数,y的值随x值的增大而 .
16.已知二元一次方程中,若x=3时,y= ;若y=1时,则x= .
17.一个汽车牌在水中的倒影为 ,则该车牌照号码为 .
18.如下图是一个简单的数值运算程序,当输入x的值为-1时,输出的数值为______.
19.已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.
(1)△BCE与哪一个三角形全等?试说明你的理由;
(2)若AB⊥BC 且BC=4,AB=6,求EF的长.
20.一次函数y=kx+4的图象经过点(-3,-2),则
(1)求这个函数表达式;
(2)判断(-5,3)是否在此函数的图象上;
(3)建立适当坐标系,画出该函数的图象.
21.如图,已知两直线l1和l2相交于点A(4,3),且OA=OB,请分别求出两条直线对应的函数关系式.
22.如图,在□ABCD中,E、F是对角线AC上的点,且AE=CF,试说明四边形BFDE是平行四边形.
23. 已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个
△DEC,且使DE∥AC,CE∥BD,试判断四边形DECP的形状并且说明理由。
24.抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库。已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨。从甲、乙两库到A、B两库的路程和运费如下表(表中“元/吨·千米”表示每吨粮食运送1千米所需人民币)
(1)若甲库运往A库粮食吨,请写出将粮食运往A、B两库的总运费(元)与(吨)的函数关系式
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
A
C
B
D
FFfFFFF
E
输出
-2
×(-3)
输入x
(第15题图)
N
M
O
O
y
x
O
x
y
O
x
y
O
y
x
(第4题)图)
0
-3
4
M
x
y
E
F
D
C
B
A
(4,0)
A
C
B
3
O
D
y
x
l2
l1
y(万元)
x(台)
y2=0.005x+0.3
y1
B
1.2
0.3
0.2
20
0
PAGE
1
同课章节目录
