1.1.1空间向量及其线性运算 课件(共32张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 08:16:58 | ||
图片预览









文档简介
(共32张PPT)
空间向量与立体几何
1.1.1空间向量及其线性运算
教学目标
一
二
三
教学目标
了解空间向量的相关概念
掌握空间向量的线性运算
掌握空间向量的线性运算与简单运用
重点
难点
重点
新知导入
在滑翔过程中,飞行员会受到来自不同方向、大小各异的力,例如绳索的拉力、风力、重力等。显然,这些力不在同一个平面内。联想用平面向量解决物理问题的方法,能否把平面向量推广到空间向量,从而利用空间向量研究滑翔运动呢
下面我们类比平面向量研究空间向量,先从空间向量的概念和表示开始。
类比
新知探究
探究一:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
新知讲解
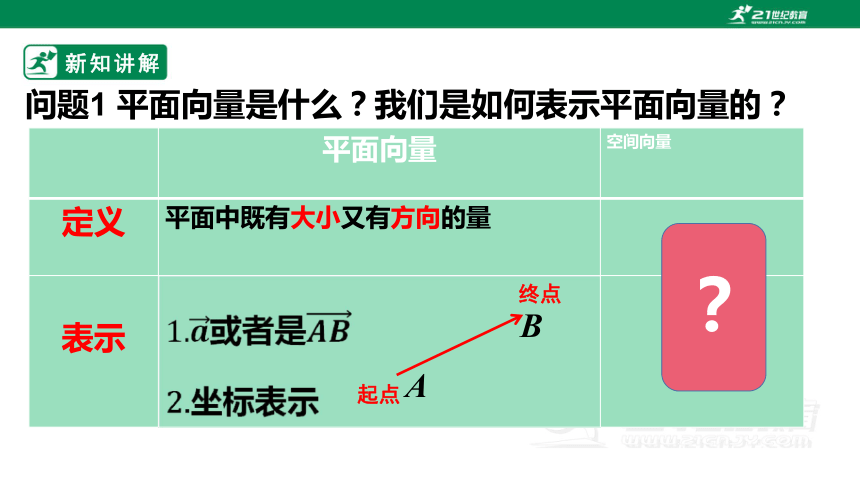
问题1 平面向量是什么?我们是如何表示平面向量的?
平面向量 空间向量
定义 平面中既有大小又有方向的量
表示
起点
终点
?
概念生成
空间向量的概念是什么?
平面向量 空间向量
定义 平面中既有大小又有方向的量 空间中既有大小又有方向的量
表示 新知讲解
问题2 你能回忆起平面向量中相关概念吗?
平面向量 空间向量
零向量 单位向量 相等向量 相反向量 共线向量 方向相同或相反的向量叫做共线向量,(平行向量),记 零向量与任意向量共线
长度为0的向量,记作:
模为1的向量.
模相等,方向相同的向量。记:
模相等,方向相反的向量。记:
概念的本质是一样的
新知探究
探究二:我们学面向量相关的概念后,学面向量的线性运算,我们能否类比平面向量的线性运算得出空间向量的线性运算?
我们一起回忆一下平面向量的线性运算,类比的得出空间向量线性运算
新知讲解
问题3 平面向量的线性运算有哪些?我们当时是如何探究这些运算?
加法,减法,数乘
定义
法则
运算律
新知讲解
问题4 请大家以小组形式进行讨论
1.回忆出平面向量的加减法运算及其运算法则,还有平面向量的运算律有哪些?
2.空间向量的加减法及其法则,运算与平面向量是否一致?
比一比,看哪个小组列出又快又准!
概念生成
平面向量 空间向量
加减法 定义:求两个平面向量的和与差的运算. 法则:三角形法则和平行四边形法则 与平面向量加减法一致
概念生成
平面向量 空间向量
数乘运算 概念生成
平面向量 空间向量
运算法则
交换律:
结合律
分配律
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
新知讲解
问题4 请大家思考下,下面的结合律是该如何解释?
A
B
C
D
A1
B1
C1
D1
体对角线
新知探究
探究三 平面向量的线性运算可以解决平面中许多问题,那空间向量的线性运算能解决空间中哪些问题?
新知讲解
问题5 平面向量解决哪些问题?
平行,垂直,模长,角
新知讲解
问题6 平面中两个共线向量的充要条件是什么?
直线的方向向量
空间向量同样适用
概念生成
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
1.向量可以进行平移
2.平行即共面
新知讲解
问题7 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
1.向量可以进行平移
2.平面向量基本定理也可以是共面向量定理
概念生成
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
(3)判断三个向量是否共面
A
B
C
D
A1
B1
C1
D1
新知讲解
问题8 A,B,P三点共线的充要条件是什么?
问题9 P与A,B,C四点共面的充要条件是什么?
请同学们课后将推导过程详细描述,加分哟!~
类比与对比
概念生成
课堂练习
例1 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
证明:
·
选择恰当的向量表示问题中的几何元素,通过向量运算得出几何元素的关系,是用向量解决立体几何问题的常用方法.
课堂练习
向量的加法运算!
课堂练习
加法
减法
对角线
课堂总结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
作业布置
作业答案
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
空间向量与立体几何
1.1.1空间向量及其线性运算
教学目标
一
二
三
教学目标
了解空间向量的相关概念
掌握空间向量的线性运算
掌握空间向量的线性运算与简单运用
重点
难点
重点
新知导入
在滑翔过程中,飞行员会受到来自不同方向、大小各异的力,例如绳索的拉力、风力、重力等。显然,这些力不在同一个平面内。联想用平面向量解决物理问题的方法,能否把平面向量推广到空间向量,从而利用空间向量研究滑翔运动呢
下面我们类比平面向量研究空间向量,先从空间向量的概念和表示开始。
类比
新知探究
探究一:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
新知讲解
问题1 平面向量是什么?我们是如何表示平面向量的?
平面向量 空间向量
定义 平面中既有大小又有方向的量
表示
起点
终点
?
概念生成
空间向量的概念是什么?
平面向量 空间向量
定义 平面中既有大小又有方向的量 空间中既有大小又有方向的量
表示 新知讲解
问题2 你能回忆起平面向量中相关概念吗?
平面向量 空间向量
零向量 单位向量 相等向量 相反向量 共线向量 方向相同或相反的向量叫做共线向量,(平行向量),记 零向量与任意向量共线
长度为0的向量,记作:
模为1的向量.
模相等,方向相同的向量。记:
模相等,方向相反的向量。记:
概念的本质是一样的
新知探究
探究二:我们学面向量相关的概念后,学面向量的线性运算,我们能否类比平面向量的线性运算得出空间向量的线性运算?
我们一起回忆一下平面向量的线性运算,类比的得出空间向量线性运算
新知讲解
问题3 平面向量的线性运算有哪些?我们当时是如何探究这些运算?
加法,减法,数乘
定义
法则
运算律
新知讲解
问题4 请大家以小组形式进行讨论
1.回忆出平面向量的加减法运算及其运算法则,还有平面向量的运算律有哪些?
2.空间向量的加减法及其法则,运算与平面向量是否一致?
比一比,看哪个小组列出又快又准!
概念生成
平面向量 空间向量
加减法 定义:求两个平面向量的和与差的运算. 法则:三角形法则和平行四边形法则 与平面向量加减法一致
概念生成
平面向量 空间向量
数乘运算 概念生成
平面向量 空间向量
运算法则
交换律:
结合律
分配律
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
新知讲解
问题4 请大家思考下,下面的结合律是该如何解释?
A
B
C
D
A1
B1
C1
D1
体对角线
新知探究
探究三 平面向量的线性运算可以解决平面中许多问题,那空间向量的线性运算能解决空间中哪些问题?
新知讲解
问题5 平面向量解决哪些问题?
平行,垂直,模长,角
新知讲解
问题6 平面中两个共线向量的充要条件是什么?
直线的方向向量
空间向量同样适用
概念生成
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
1.向量可以进行平移
2.平行即共面
新知讲解
问题7 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
1.向量可以进行平移
2.平面向量基本定理也可以是共面向量定理
概念生成
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
(3)判断三个向量是否共面
A
B
C
D
A1
B1
C1
D1
新知讲解
问题8 A,B,P三点共线的充要条件是什么?
问题9 P与A,B,C四点共面的充要条件是什么?
请同学们课后将推导过程详细描述,加分哟!~
类比与对比
概念生成
课堂练习
例1 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
证明:
·
选择恰当的向量表示问题中的几何元素,通过向量运算得出几何元素的关系,是用向量解决立体几何问题的常用方法.
课堂练习
向量的加法运算!
课堂练习
加法
减法
对角线
课堂总结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
作业布置
作业答案
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
