1.1.2空间向量数量积的运算 课件(共23张PPT)
文档属性
| 名称 | 1.1.2空间向量数量积的运算 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 08:29:44 | ||
图片预览





文档简介
(共23张PPT)
空间向量与立体几何
1.1.2空间向量数量积的运算
复习回顾
问题1
(1)空间中共线向量的定理是什么?
(2)共面向量基本定理于是什么?
(3)四点共面的充要条件是什么?
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
新知导入
平面向量及其线性运算
空间向量及线性运算
推广
平面向量数量积运算
空间向量数量积运算
推广
类比与转化
教学目标
一
二
三
教学目标
经历平面向量数量积转化到空间向量数量积的过程
掌握空间向量数量积与运算律
掌握空间向量数量积的简单运用
重点
难点
重点
新知探究
探究一:类比平面向量的数量积运算,将平面向量数量积推广到空间数量积的运算
新知讲解
问题2 回忆平面向量的知识,我们当时是如何研究它的数量积运算?
定义夹角
数量积定义
运算律
运用
新知讲解
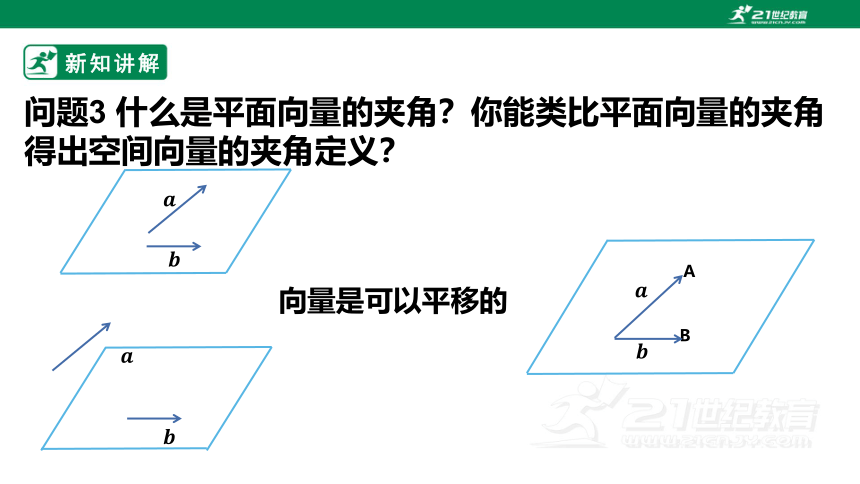
问题3 什么是平面向量的夹角?你能类比平面向量的夹角得出空间向量的夹角定义?
B
A
向量是可以平移的
概念生成
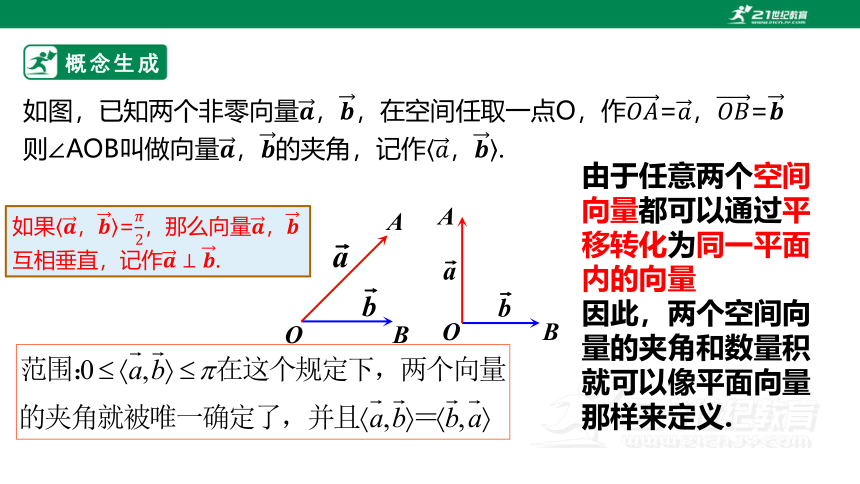
如图,已知两个非零向量,在空间任取一点O,作=,=
则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量
因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
新知讲解
问题4 平面向量的数量积是什么?类比平面向量数量积得出空间向量的数量积运算。
平面向量的数量积:
由于我们也定义了空间夹角,所以这也空间向量的数量积
概念生成
空间向量的数量积:
零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
=||||cos=
注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
新知讲解
问题5 在平面向量的学习中,我们学习了向量的投影.
(1)类似地,在空间,向量向向量的投影有什么意义?
(2)向量向直线的投影呢?
(3)向量向平面的投影呢?
概念生成
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=cos,向量称为向量量在向量上的投影向量.类似地,可以将向量向直线投影(图(2)).
图(1)
图(2)
β
图(3)
如图(3),向量向平面β投影,就是分别由向量的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量,向量称为向量在平面β上的投影向量.这时,向量,的夹角就是向量所在直线与平面β所成的角.
新知探究
探究二 空间向量的数量积运算律有哪些?与平面向量数量积运算律是否一致?
一致!
概念生成
空间向量的数量积满足如下的运算律:
()·=(·),∈R
=(交换律)
·(+)=+·(分配律)
问题6 如何证明分配律?
新知讲解
(1)对于三个均不为0的数,若ab=ac,则b=c.
对于向量,,,由=,你能得到=吗 如果不能,请举出反例.
(2)对于三个均不为0的数,b、c ,若ab=c,则a=(或b=).
对于向量,,若=k,能不能写成(或)的形式
(3)对于三个均不为0的数a,b,c,有(ab )c =a(bc).
对于向量,()=()成立吗 为什么
请同学们以小组形式讨论上面的三个问题,并给出解释
(数形结合)
课堂练习
A
B
C
D
课堂练习
3.已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
A
B
C
D
解析:(1)·=||| cos<,>=5×4×cos 60°=10;
(2)因为=+
||===
(3)因为=5×3×cos 60°=,=3×4×cos 90°=0
所以=(++)
=+++2(·+·+·)
=+++2(0+10+)=85=.
新知探究
探究三 利用空间向量数量积运算,能够解决空间中哪些问题?
新知讲解
问题7 平面向量数量积可以解决哪些问题?空间向量是否可以解决同样的问题?
模长,角,平行,垂直
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来
,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
课堂练习
l
m
n
g
证明:在平面α内作任意一条直线,分别在直线
, , 上取非零向量,, , .
因为直线与相交,所以向量, ,不平行.由向量共面的充要条件可知,存在唯一的有序实效对(,),使
=.
将上式两边分别与向量作数量积运算,得
=,
因为=0,=0(为什么 ),所以 =0.所以.
这就证明了直线垂直于平面α内的任意一条直线,所以平面α.
用向量表示直线
用数量积为0描述垂直
课堂总结
1、空间向量数量积的定义:
2、向量数量积的性质
4、空间向量的数量积满足如下的运算律
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
空间向量与立体几何
1.1.2空间向量数量积的运算
复习回顾
问题1
(1)空间中共线向量的定理是什么?
(2)共面向量基本定理于是什么?
(3)四点共面的充要条件是什么?
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
新知导入
平面向量及其线性运算
空间向量及线性运算
推广
平面向量数量积运算
空间向量数量积运算
推广
类比与转化
教学目标
一
二
三
教学目标
经历平面向量数量积转化到空间向量数量积的过程
掌握空间向量数量积与运算律
掌握空间向量数量积的简单运用
重点
难点
重点
新知探究
探究一:类比平面向量的数量积运算,将平面向量数量积推广到空间数量积的运算
新知讲解
问题2 回忆平面向量的知识,我们当时是如何研究它的数量积运算?
定义夹角
数量积定义
运算律
运用
新知讲解
问题3 什么是平面向量的夹角?你能类比平面向量的夹角得出空间向量的夹角定义?
B
A
向量是可以平移的
概念生成
如图,已知两个非零向量,在空间任取一点O,作=,=
则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量
因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
新知讲解
问题4 平面向量的数量积是什么?类比平面向量数量积得出空间向量的数量积运算。
平面向量的数量积:
由于我们也定义了空间夹角,所以这也空间向量的数量积
概念生成
空间向量的数量积:
零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
=||||cos=
注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
新知讲解
问题5 在平面向量的学习中,我们学习了向量的投影.
(1)类似地,在空间,向量向向量的投影有什么意义?
(2)向量向直线的投影呢?
(3)向量向平面的投影呢?
概念生成
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=cos,向量称为向量量在向量上的投影向量.类似地,可以将向量向直线投影(图(2)).
图(1)
图(2)
β
图(3)
如图(3),向量向平面β投影,就是分别由向量的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量,向量称为向量在平面β上的投影向量.这时,向量,的夹角就是向量所在直线与平面β所成的角.
新知探究
探究二 空间向量的数量积运算律有哪些?与平面向量数量积运算律是否一致?
一致!
概念生成
空间向量的数量积满足如下的运算律:
()·=(·),∈R
=(交换律)
·(+)=+·(分配律)
问题6 如何证明分配律?
新知讲解
(1)对于三个均不为0的数,若ab=ac,则b=c.
对于向量,,,由=,你能得到=吗 如果不能,请举出反例.
(2)对于三个均不为0的数,b、c ,若ab=c,则a=(或b=).
对于向量,,若=k,能不能写成(或)的形式
(3)对于三个均不为0的数a,b,c,有(ab )c =a(bc).
对于向量,()=()成立吗 为什么
请同学们以小组形式讨论上面的三个问题,并给出解释
(数形结合)
课堂练习
A
B
C
D
课堂练习
3.已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
A
B
C
D
解析:(1)·=||| cos<,>=5×4×cos 60°=10;
(2)因为=+
||===
(3)因为=5×3×cos 60°=,=3×4×cos 90°=0
所以=(++)
=+++2(·+·+·)
=+++2(0+10+)=85=.
新知探究
探究三 利用空间向量数量积运算,能够解决空间中哪些问题?
新知讲解
问题7 平面向量数量积可以解决哪些问题?空间向量是否可以解决同样的问题?
模长,角,平行,垂直
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来
,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
课堂练习
l
m
n
g
证明:在平面α内作任意一条直线,分别在直线
, , 上取非零向量,, , .
因为直线与相交,所以向量, ,不平行.由向量共面的充要条件可知,存在唯一的有序实效对(,),使
=.
将上式两边分别与向量作数量积运算,得
=,
因为=0,=0(为什么 ),所以 =0.所以.
这就证明了直线垂直于平面α内的任意一条直线,所以平面α.
用向量表示直线
用数量积为0描述垂直
课堂总结
1、空间向量数量积的定义:
2、向量数量积的性质
4、空间向量的数量积满足如下的运算律
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
