湖南省怀化市鹤城区2021-2022学年八年级下学期期末教学质量检测数学试题(word版含解析)
文档属性
| 名称 | 湖南省怀化市鹤城区2021-2022学年八年级下学期期末教学质量检测数学试题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 787.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 21:29:04 | ||
图片预览


文档简介
怀化市鹤城区2022年上期期末教学质量检测
八年级数学
考生注意:1.本试卷三道大题。考试时间120分钟,满分150分。
2.本套试卷分试题卷和答题卡,请在答题卡上作答。
一、选择题(每小题4分,共40分)
1.下列垃圾分类的标志中,既是轴对称图形又是中心对称图形的是
(
其他垃圾物
) (
厨余垃圾
) (
有害垃圾
) (
可回收物
)A. B. C. D.
2.某校对八年级(1)班50名学生进行体能评定,进行了“立定跳远”、“实心球”、“跑步”的测试,根据测试总成绩划分体能等级,等级分为“优秀”、“良好”、“合格”、“较差”四个等级,该班级“优秀”的有28人,“良好”的有15人,“合格”的有5人,则该班级学生这次体能评定为“较差”的频率是
A.2 B.0.02 C.4 D.0.04
3.点P在第二象限内,P点到x、y轴的距离分别是4、3,则点P的坐标为
A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)
4.“百日长跑”是一项非常有益身心的体育活动,体育老师一声令下,小雅立即开始慢慢加速,途中一直保持匀速,最后150米时奋力冲刺跑完全程,下列最符合小雅跑步时的速度y(单位:米/分)与时间x(单位:分)之间的大致图象的是
A. B. C. D.
5.一次函数,当系数时,其图象大致是
A. B. C. D.
6.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0),(5,0),(2,3)则顶点C的坐标为
A.(7,3) B.(5,3) C.(3,7) D.(8,2)
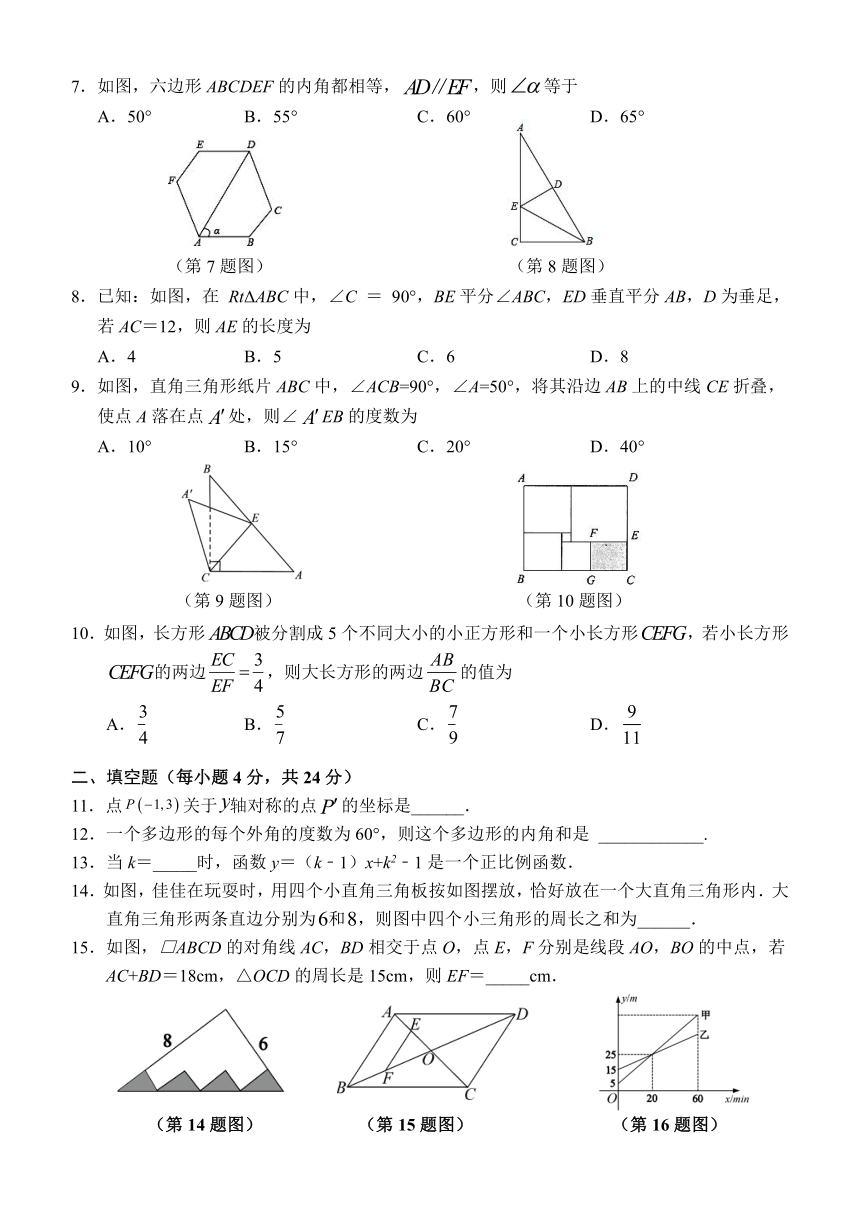
7.如图,六边形ABCDEF的内角都相等,,则等于
A.50° B.55° C.60° D.65°
(第7题图) (第8题图)
8.已知:如图,在 RtΔABC中,∠C = 90°,BE平分∠ABC,ED垂直平分AB,D为垂足,若AC=12,则AE的长度为
A.4 B.5 C.6 D.8
9.如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点处,则∠EB的度数为
A.10° B.15° C.20° D.40°
(第9题图) (第10题图)
10.如图,长方形被分割成5个不同大小的小正方形和一个小长方形,若小长方形的两边,则大长方形的两边的值为
A. B. C. D.
二、填空题(每小题4分,共24分)
11.点关于轴对称的点的坐标是______.
12.一个多边形的每个外角的度数为60°,则这个多边形的内角和是 ____________.
13.当k=_____时,函数y=(k﹣1)x+k2﹣1是一个正比例函数.
14.如图,佳佳在玩耍时,用四个小直角三角板按如图摆放,恰好放在一个大直角三角形内.大直角三角形两条直边分别为和,则图中四个小三角形的周长之和为______.
15.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=18cm,△OCD的周长是15cm,则EF=_____cm.
(第14题图) (第15题图) (第16题图)
16.甲、乙两只气球分别从不同高度同时匀速上升,气球所在位置距离地面的高度(单位)与气球上升的时间(单位)之间的函数关系如图所示.下列说法:①甲气球上升过程中与的函数关系为:;②时,甲气球在乙气球上方;③两气球高度差为时,上升时间为;④上升时,乙气球距离地面高度为.其中错误的有_______.(将所有错误的序号都填上)
三、解答题(8个小题,共86分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC向下平移3个单位,再向右平移4个单位得到△A'B'C';请画出平移后的△A'B'C'及写出A'、B'、C'的坐标.
18.(8分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论
(
c
)
19.(10分)如图,平行四边形ABCD中,BD为对角线,过BD的中点O作直线EF,分别交BA、DC的延长线于点E、F.求证:AE=CF.
20.(10分)怀化市某广场对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米.求这块地草坪绿化的费用.
21.(12分)某校体育老师为了研究八年级学生800m赛跑后学生心率的分布情况,随机抽取了该年级45名学生,测量了他们赛跑后1的脉搏次数,结果如下:
132 136 138 141 143 144 144 146 146 147 148 149 149 151 151
152 153 153 154 154 154 156 156 157 157 157 158 158 158 159
159 159 159 161 161 162 162 163 163 164 164 164 164 166 166
(1)该调查中的个体是____________ ;
(2)该老师将上述数据分组后,列出了频数分布
表,请将频数分布表补充完整;
(3)根据频数分布表画出频数分布直方图.
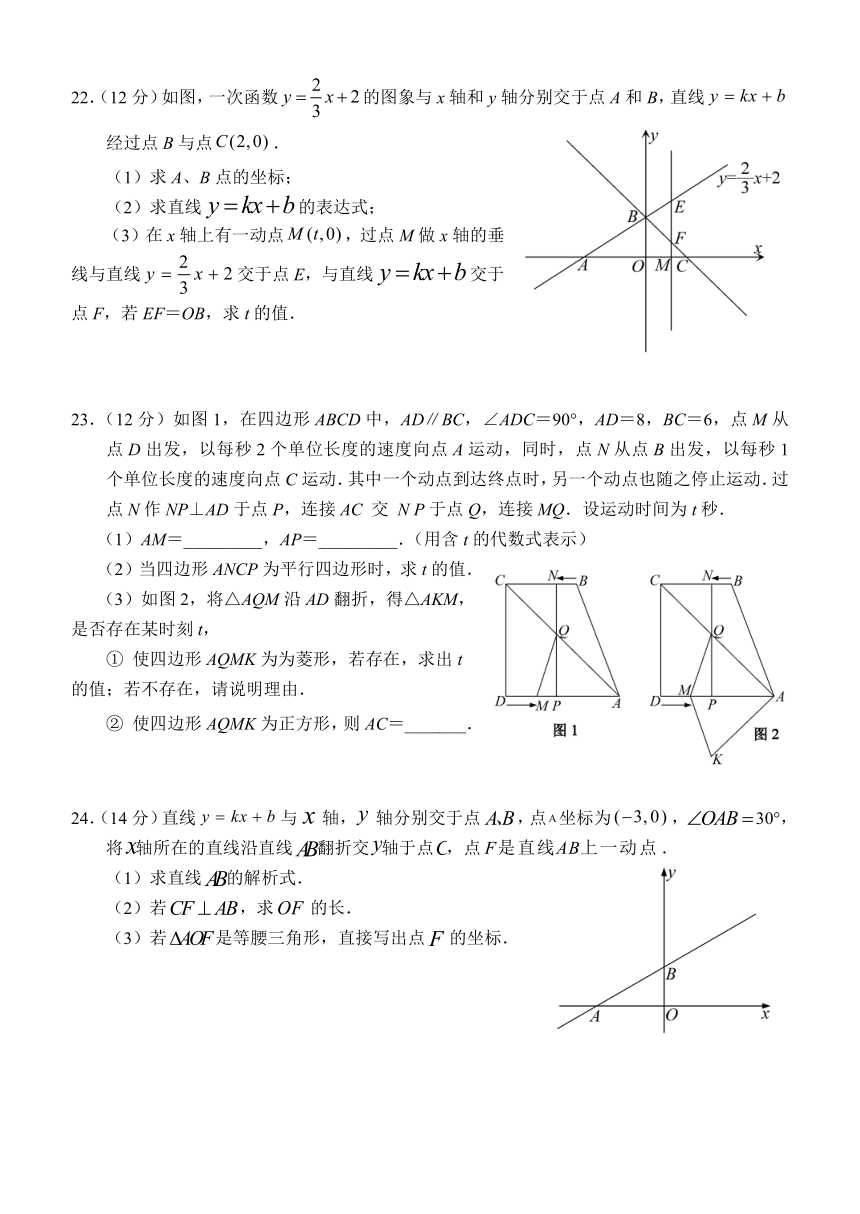
22.(12分)如图,一次函数的图象与x轴和y轴分别交于点A和B,直线经过点B与点.
(1)求A、B点的坐标;
(2)求直线的表达式;
(3)在x轴上有一动点,过点M做x轴的垂线与直线交于点E,与直线交于点F,若EF=OB,求t的值.
23.(12分)如图1,在四边形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC 交 N P于点Q,连接MQ.设运动时间为t秒.
(1)AM=_________,AP=_________.(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值.
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
① 使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由.
② 使四边形AQMK为正方形,则AC=_______.
24.(14分)直线与轴,轴分别交于点,点坐标为,30°,将轴所在的直线沿直线翻折交轴于点,点.
(1)求直线的解析式.
(2)若,求的长.
(3)若是等腰三角形,直接写出点的坐标.
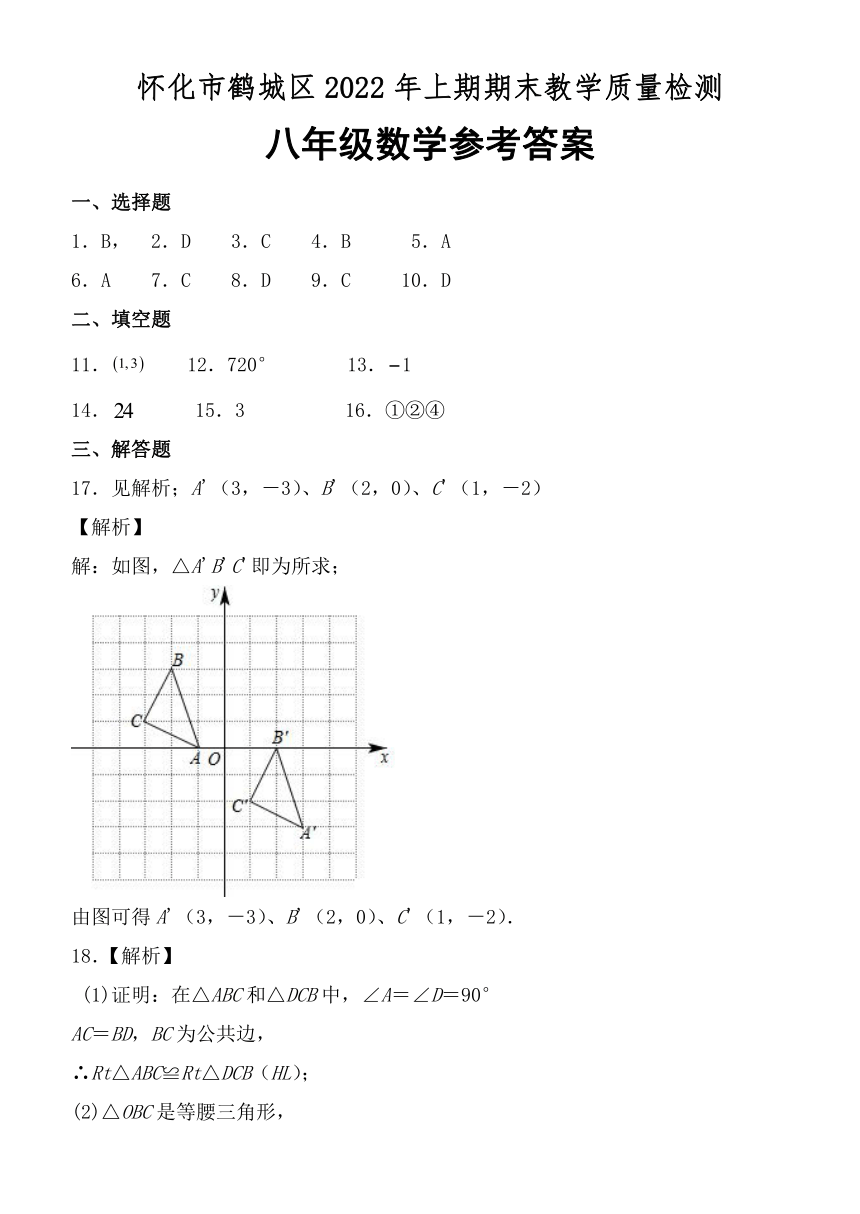
怀化市鹤城区2022年上期期末教学质量检测
八年级数学参考答案
一、选择题
1.B, 2.D 3.C 4.B 5.A
6.A 7.C 8.D 9.C 10.D
二、填空题
11. 12.720° 13. 1
14. 15.3 16.①②④
三、解答题
17.见解析;A'(3,-3)、B'(2,0)、C'(1,-2)
【解析】
解:如图,△A'B'C'即为所求;
由图可得A'(3,-3)、B'(2,0)、C'(1,-2).
18.【解析】
(1)证明:在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
证明:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
19.【解析】
解:∵四边形ABCD是平行四边形,
∴,AB=CD
∴∠EBO=∠FDO,∠BEO=∠DFO,
∵O是BD的中点,
∴OB=OD,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(AAS),
∴BE=DF,
∴BE-AB=DF-CF,
∴AE=CF.
20.3600元
【解析】
解:连接AC,,
∵,
∴△ABC是直角三角形,∠ACB=90°,
∴,
(元).
答:这块地草坪绿化的价钱为3600元.
21.(1)该年级每名学生赛跑后1的脉搏次数;(2)142;2;142;5;(3)作图见解析.
【解析】
解:(1)该年级每名学生赛跑后1的脉搏次数;
故答案为该年级每名学生赛跑后1min的脉搏次数;
(2)根据组距为5,可得各组的分界值,根据频数统计可得各组频数,
故答案为:142,142,2,5;
(3)频率分布直方图如图所示.
22.(1)A(-3,0),B(0,2);
(2)y=-x+2;
(3)
【解析】
(1)解:令x=0,则y=2,
令y=0,则,解得:x=-3,
∴点A(-3,0),B(0,2);
(2)解:把点B(0,2),代入,得:
,解得:,
∴直线的表达式为y=-x+2;
(3)解:∵点,
∴点,
∴,
∵点B(0,2),
∴OB=2,
∵EF=OB,
∴,解得:.
23.(1)8﹣2t,2+t.
(2)t=2
(3)①t=1;②
【解析】解:由题意得BN=t,DM=2t,
∴AM=AD-DM=8-2t
∵,∠ADC=90°,
∴∠BCD=90°,
∵NP⊥AD,
∴四边形CNPD为矩形
∴DP=CN=BC﹣BN=6﹣t,
∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)
解:∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),
解得t=2,
(3)
解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:
连接PK,
由翻折的性质可得PQ=PK(因为QP⊥AP)
∵NP⊥AD,QP=PK
∴当PM=PA时有四边形AQMK为菱形
∴6﹣t﹣2t=8﹣(6﹣t),
解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°,
∴∠CAD=45°
∴四边形AQMK为正方形,则CD=AD,
∵AD=8,
∴CD=8,
∴AC=.
故答案为
24.(1);
(2)3;
(3)(,)或( ,)或(,)或( ,)
【解析】(1)
解:∵A的坐标为(,0),
∴AO=3,
∵ , ,
∴AB=2OB,
由勾股定理知 ,
∴ ,
∴B(0, ),
把A(,0),B(0, )代入y=kx+b,
得 ,
∴ ,
∴直线AB解析式为;
(2)解:延长CF交x轴于点G,
∵翻折,
∴∠CAF=∠BAO=30°,
∴∠CAG=60°,
∴∠ACO=30°,
∴AC=2AO=6,
∵
∴ ,
在△ACF和△AGF中,
,
∴ ,
∴AC=AG=6,
∴AG=2AO,
∴AO=GO,
∴
(3)当AF=OF时,如下图,过F作于H
则AH=OH=,
又∠BAO=30°,
∴AF=2FH,
由勾股定理得 ,
∴,
F(,);
当AO=OF=3时,如下图,过F作于M,
则∠AFO=∠FAO=30°,
∴∠FOM=∠AFO+∠FAO=60°,
∴∠OFM=30°,
∴ ,
∴ ,
∴F的坐标为( ,);
当AF=AO=3时,
F在A的右侧时,如图1,过F作于N,
∵∠BAO=30°,
∴ ,
∴ ,
∴ ,
∴F的坐标为(,);
F在A的左侧时,如图2,过F作于K,
∵∠BAO=30°,
∴∠FAK=30°,
∴ ,
∴ ,
∴ ,
∴F的坐标为( ,).
综上,F的坐标为(,)或( ,)或(,)或( ,).
八年级数学
考生注意:1.本试卷三道大题。考试时间120分钟,满分150分。
2.本套试卷分试题卷和答题卡,请在答题卡上作答。
一、选择题(每小题4分,共40分)
1.下列垃圾分类的标志中,既是轴对称图形又是中心对称图形的是
(
其他垃圾物
) (
厨余垃圾
) (
有害垃圾
) (
可回收物
)A. B. C. D.
2.某校对八年级(1)班50名学生进行体能评定,进行了“立定跳远”、“实心球”、“跑步”的测试,根据测试总成绩划分体能等级,等级分为“优秀”、“良好”、“合格”、“较差”四个等级,该班级“优秀”的有28人,“良好”的有15人,“合格”的有5人,则该班级学生这次体能评定为“较差”的频率是
A.2 B.0.02 C.4 D.0.04
3.点P在第二象限内,P点到x、y轴的距离分别是4、3,则点P的坐标为
A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)
4.“百日长跑”是一项非常有益身心的体育活动,体育老师一声令下,小雅立即开始慢慢加速,途中一直保持匀速,最后150米时奋力冲刺跑完全程,下列最符合小雅跑步时的速度y(单位:米/分)与时间x(单位:分)之间的大致图象的是
A. B. C. D.
5.一次函数,当系数时,其图象大致是
A. B. C. D.
6.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0),(5,0),(2,3)则顶点C的坐标为
A.(7,3) B.(5,3) C.(3,7) D.(8,2)
7.如图,六边形ABCDEF的内角都相等,,则等于
A.50° B.55° C.60° D.65°
(第7题图) (第8题图)
8.已知:如图,在 RtΔABC中,∠C = 90°,BE平分∠ABC,ED垂直平分AB,D为垂足,若AC=12,则AE的长度为
A.4 B.5 C.6 D.8
9.如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点处,则∠EB的度数为
A.10° B.15° C.20° D.40°
(第9题图) (第10题图)
10.如图,长方形被分割成5个不同大小的小正方形和一个小长方形,若小长方形的两边,则大长方形的两边的值为
A. B. C. D.
二、填空题(每小题4分,共24分)
11.点关于轴对称的点的坐标是______.
12.一个多边形的每个外角的度数为60°,则这个多边形的内角和是 ____________.
13.当k=_____时,函数y=(k﹣1)x+k2﹣1是一个正比例函数.
14.如图,佳佳在玩耍时,用四个小直角三角板按如图摆放,恰好放在一个大直角三角形内.大直角三角形两条直边分别为和,则图中四个小三角形的周长之和为______.
15.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=18cm,△OCD的周长是15cm,则EF=_____cm.
(第14题图) (第15题图) (第16题图)
16.甲、乙两只气球分别从不同高度同时匀速上升,气球所在位置距离地面的高度(单位)与气球上升的时间(单位)之间的函数关系如图所示.下列说法:①甲气球上升过程中与的函数关系为:;②时,甲气球在乙气球上方;③两气球高度差为时,上升时间为;④上升时,乙气球距离地面高度为.其中错误的有_______.(将所有错误的序号都填上)
三、解答题(8个小题,共86分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC向下平移3个单位,再向右平移4个单位得到△A'B'C';请画出平移后的△A'B'C'及写出A'、B'、C'的坐标.
18.(8分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论
(
c
)
19.(10分)如图,平行四边形ABCD中,BD为对角线,过BD的中点O作直线EF,分别交BA、DC的延长线于点E、F.求证:AE=CF.
20.(10分)怀化市某广场对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米.求这块地草坪绿化的费用.
21.(12分)某校体育老师为了研究八年级学生800m赛跑后学生心率的分布情况,随机抽取了该年级45名学生,测量了他们赛跑后1的脉搏次数,结果如下:
132 136 138 141 143 144 144 146 146 147 148 149 149 151 151
152 153 153 154 154 154 156 156 157 157 157 158 158 158 159
159 159 159 161 161 162 162 163 163 164 164 164 164 166 166
(1)该调查中的个体是____________ ;
(2)该老师将上述数据分组后,列出了频数分布
表,请将频数分布表补充完整;
(3)根据频数分布表画出频数分布直方图.
22.(12分)如图,一次函数的图象与x轴和y轴分别交于点A和B,直线经过点B与点.
(1)求A、B点的坐标;
(2)求直线的表达式;
(3)在x轴上有一动点,过点M做x轴的垂线与直线交于点E,与直线交于点F,若EF=OB,求t的值.
23.(12分)如图1,在四边形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC 交 N P于点Q,连接MQ.设运动时间为t秒.
(1)AM=_________,AP=_________.(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值.
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
① 使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由.
② 使四边形AQMK为正方形,则AC=_______.
24.(14分)直线与轴,轴分别交于点,点坐标为,30°,将轴所在的直线沿直线翻折交轴于点,点.
(1)求直线的解析式.
(2)若,求的长.
(3)若是等腰三角形,直接写出点的坐标.
怀化市鹤城区2022年上期期末教学质量检测
八年级数学参考答案
一、选择题
1.B, 2.D 3.C 4.B 5.A
6.A 7.C 8.D 9.C 10.D
二、填空题
11. 12.720° 13. 1
14. 15.3 16.①②④
三、解答题
17.见解析;A'(3,-3)、B'(2,0)、C'(1,-2)
【解析】
解:如图,△A'B'C'即为所求;
由图可得A'(3,-3)、B'(2,0)、C'(1,-2).
18.【解析】
(1)证明:在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
证明:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
19.【解析】
解:∵四边形ABCD是平行四边形,
∴,AB=CD
∴∠EBO=∠FDO,∠BEO=∠DFO,
∵O是BD的中点,
∴OB=OD,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(AAS),
∴BE=DF,
∴BE-AB=DF-CF,
∴AE=CF.
20.3600元
【解析】
解:连接AC,,
∵,
∴△ABC是直角三角形,∠ACB=90°,
∴,
(元).
答:这块地草坪绿化的价钱为3600元.
21.(1)该年级每名学生赛跑后1的脉搏次数;(2)142;2;142;5;(3)作图见解析.
【解析】
解:(1)该年级每名学生赛跑后1的脉搏次数;
故答案为该年级每名学生赛跑后1min的脉搏次数;
(2)根据组距为5,可得各组的分界值,根据频数统计可得各组频数,
故答案为:142,142,2,5;
(3)频率分布直方图如图所示.
22.(1)A(-3,0),B(0,2);
(2)y=-x+2;
(3)
【解析】
(1)解:令x=0,则y=2,
令y=0,则,解得:x=-3,
∴点A(-3,0),B(0,2);
(2)解:把点B(0,2),代入,得:
,解得:,
∴直线的表达式为y=-x+2;
(3)解:∵点,
∴点,
∴,
∵点B(0,2),
∴OB=2,
∵EF=OB,
∴,解得:.
23.(1)8﹣2t,2+t.
(2)t=2
(3)①t=1;②
【解析】解:由题意得BN=t,DM=2t,
∴AM=AD-DM=8-2t
∵,∠ADC=90°,
∴∠BCD=90°,
∵NP⊥AD,
∴四边形CNPD为矩形
∴DP=CN=BC﹣BN=6﹣t,
∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)
解:∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),
解得t=2,
(3)
解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:
连接PK,
由翻折的性质可得PQ=PK(因为QP⊥AP)
∵NP⊥AD,QP=PK
∴当PM=PA时有四边形AQMK为菱形
∴6﹣t﹣2t=8﹣(6﹣t),
解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°,
∴∠CAD=45°
∴四边形AQMK为正方形,则CD=AD,
∵AD=8,
∴CD=8,
∴AC=.
故答案为
24.(1);
(2)3;
(3)(,)或( ,)或(,)或( ,)
【解析】(1)
解:∵A的坐标为(,0),
∴AO=3,
∵ , ,
∴AB=2OB,
由勾股定理知 ,
∴ ,
∴B(0, ),
把A(,0),B(0, )代入y=kx+b,
得 ,
∴ ,
∴直线AB解析式为;
(2)解:延长CF交x轴于点G,
∵翻折,
∴∠CAF=∠BAO=30°,
∴∠CAG=60°,
∴∠ACO=30°,
∴AC=2AO=6,
∵
∴ ,
在△ACF和△AGF中,
,
∴ ,
∴AC=AG=6,
∴AG=2AO,
∴AO=GO,
∴
(3)当AF=OF时,如下图,过F作于H
则AH=OH=,
又∠BAO=30°,
∴AF=2FH,
由勾股定理得 ,
∴,
F(,);
当AO=OF=3时,如下图,过F作于M,
则∠AFO=∠FAO=30°,
∴∠FOM=∠AFO+∠FAO=60°,
∴∠OFM=30°,
∴ ,
∴ ,
∴F的坐标为( ,);
当AF=AO=3时,
F在A的右侧时,如图1,过F作于N,
∵∠BAO=30°,
∴ ,
∴ ,
∴ ,
∴F的坐标为(,);
F在A的左侧时,如图2,过F作于K,
∵∠BAO=30°,
∴∠FAK=30°,
∴ ,
∴ ,
∴ ,
∴F的坐标为( ,).
综上,F的坐标为(,)或( ,)或(,)或( ,).
同课章节目录
