数学人教A版(2019)必修第一册 3.1.2函数的表示法 课件(共45张PPT)
文档属性
| 名称 | 数学人教A版(2019)必修第一册 3.1.2函数的表示法 课件(共45张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-01 20:58:52 | ||
图片预览





文档简介
(共45张PPT)
3.1 函数及其表示
3.1.2 函数的表示法
复习回顾
函数的表示法,常用的有三种:
解析法、列表法、图象法。
解析法:把两个变量的函数关系,用一个等式来表示,这个等式叫做函数的解析式。
解析式只表示一种对应关系,与所取的字母无关。
例如:y = 2 x– 1 与 u = 2 t -1 表示同一个函数。
函数解析式一定是方程;
方程不一定是函数解析式。
一次函数:y=kx+b (k≠0)
二次函数:y=ax2+bx+c (a≠0)
可看成关于x、y的方程。
例如:x2+y2=1
复习回顾
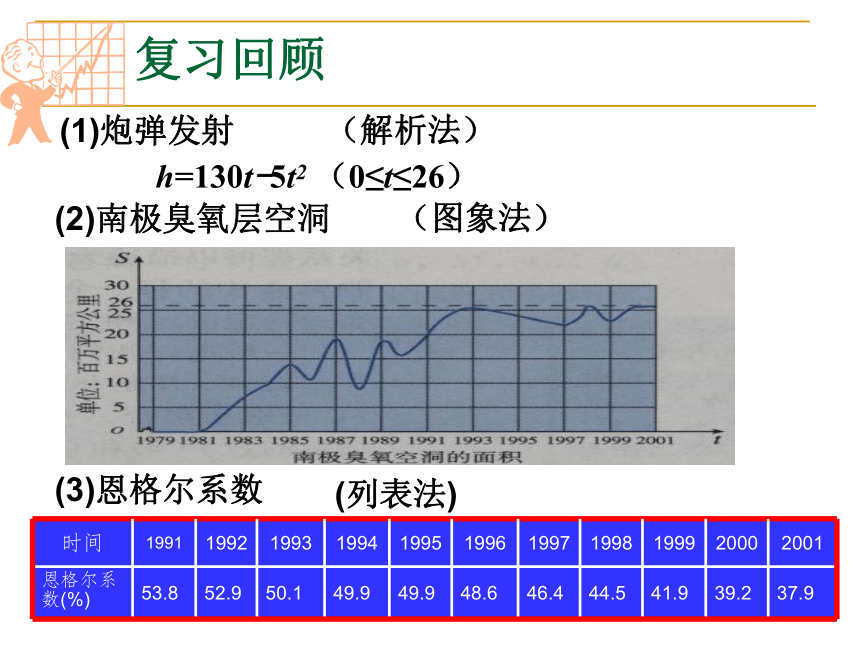
(1)炮弹发射
(解析法)
h=130t-5t2 (0≤t≤26)
(2)南极臭氧层空洞
(图象法)
(3)恩格尔系数
(列表法)
时间 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔系数(%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
函数的表示法
1、解析法:用数学表达式表示两个变量之间的对应关系.
解析式
优点:函数关系清楚,容易从自变量的值求出其对应的函数值.便于用解析式来研究函数的性质.
函数的表示法
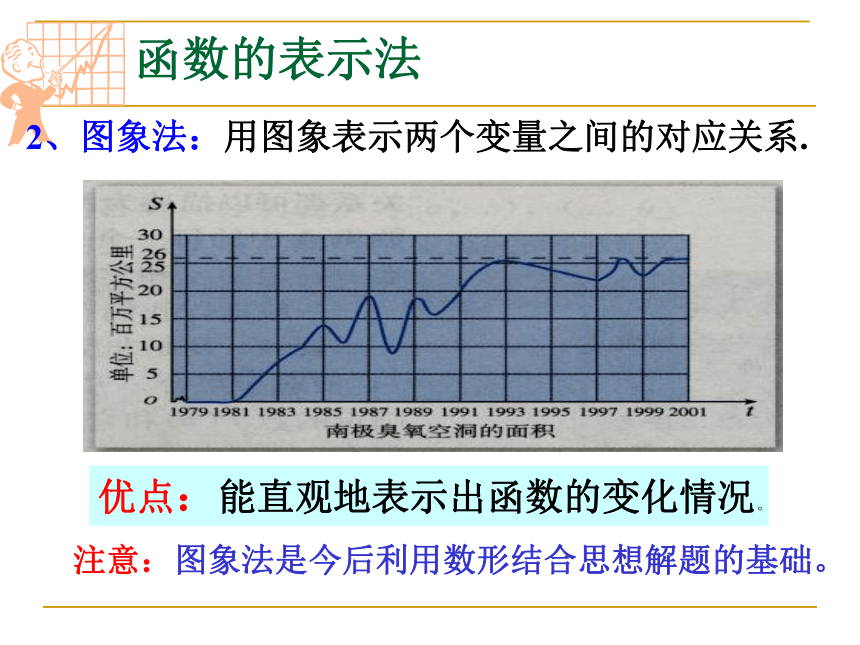
2、图象法:用图象表示两个变量之间的对应关系.
优点:能直观地表示出函数的变化情况。
注意:图象法是今后利用数形结合思想解题的基础。
图象法:
思考:初中画函数图象主要用什么方法?
利用此法画图的主要步骤如何?
初中画函数图象的主要方法是描点法。
按描点法画函数图象的主要步骤有:
(1)确定自变量 x 的取值范围,对函数图象
的整体性质有个把握;
(2)列表:选取一些典型的点,将x与y的对应值用表列出;
(3)描点:将表中点在直角坐标系中描出;
(4)连线:用平滑直线或曲线依次连接各点。
例如:
一次函数图象:一条直线——两点确定一条直线—
—找两个典型的点——通常找与坐标轴的交点。
二次函数图象:抛物线——开口方向,对称轴,顶
点,与坐标轴交点。
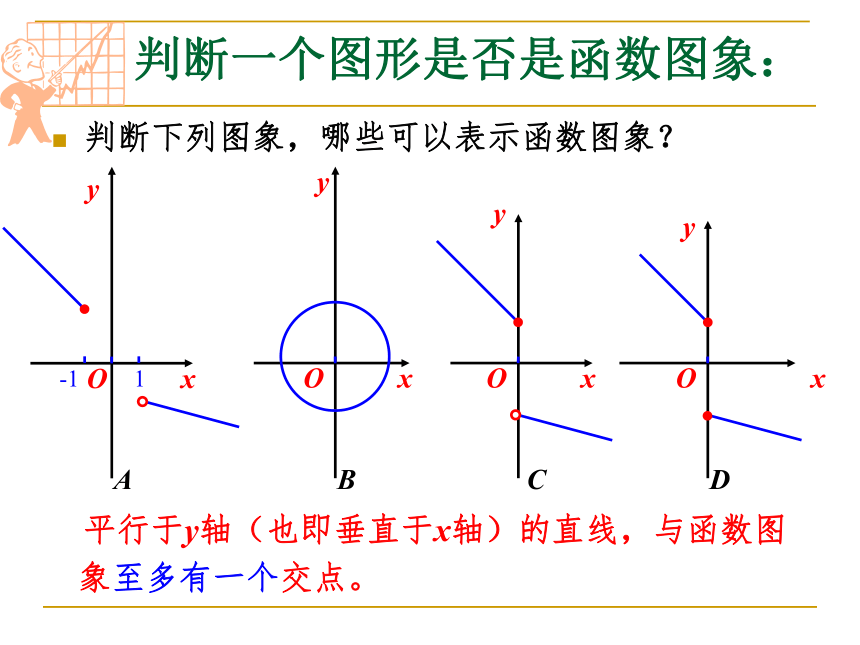
判断一个图形是否是函数图象:
判断下列图象,哪些可以表示函数图象?
x
y
O
x
y
O
x
O
x
O
y
y
A
B
C
D
平行于y轴(也即垂直于x轴)的直线,与函数图象至多有一个交点。
-1
1
函数的表示法
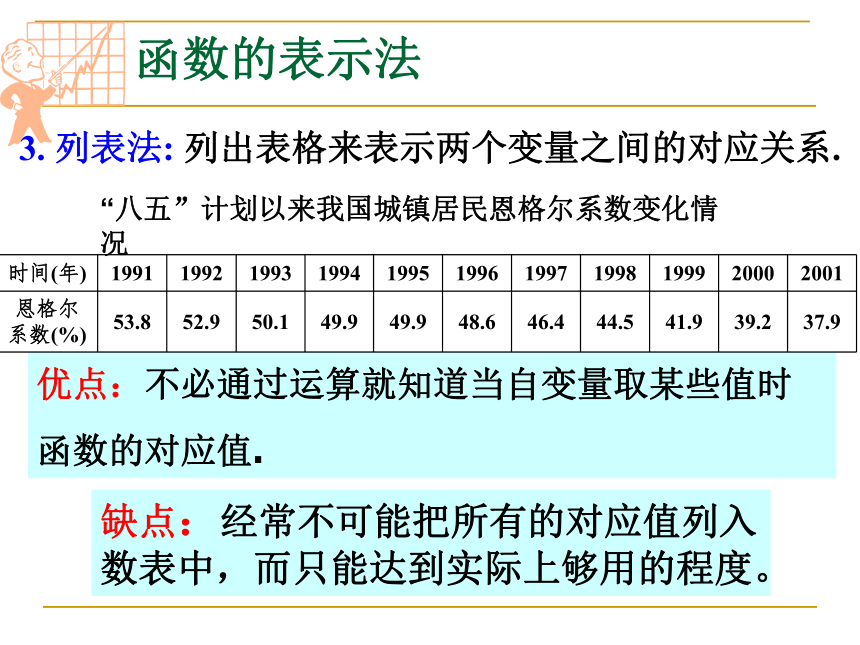
3. 列表法: 列出表格来表示两个变量之间的对应关系.
优点:不必通过运算就知道当自变量取某些值时函数的对应值.
时间(年) 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔
系数(%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
“八五”计划以来我国城镇居民恩格尔系数变化情况
缺点:经常不可能把所有的对应值列入数表中,而只能达到实际上够用的程度。
函数的表示法
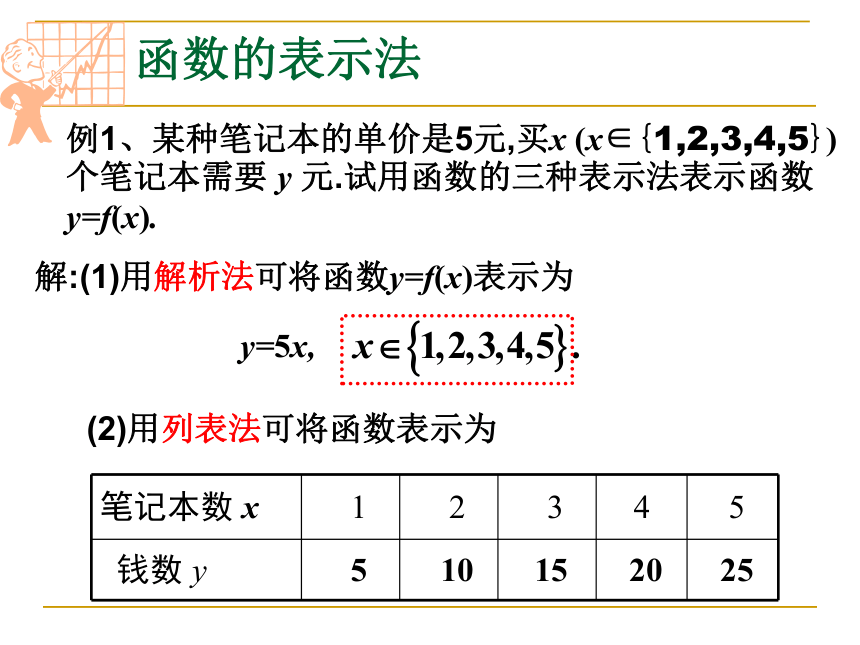
解:(1)用解析法可将函数y=f(x)表示为
y=5x,
(2)用列表法可将函数表示为
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
例1、某种笔记本的单价是5元,买x (x∈{1,2,3,4,5}) 个笔记本需要 y 元.试用函数的三种表示法表示函数y=f(x).
函数的表示法
x
y
o
5
10
15
20
25
1
2
3
4
5
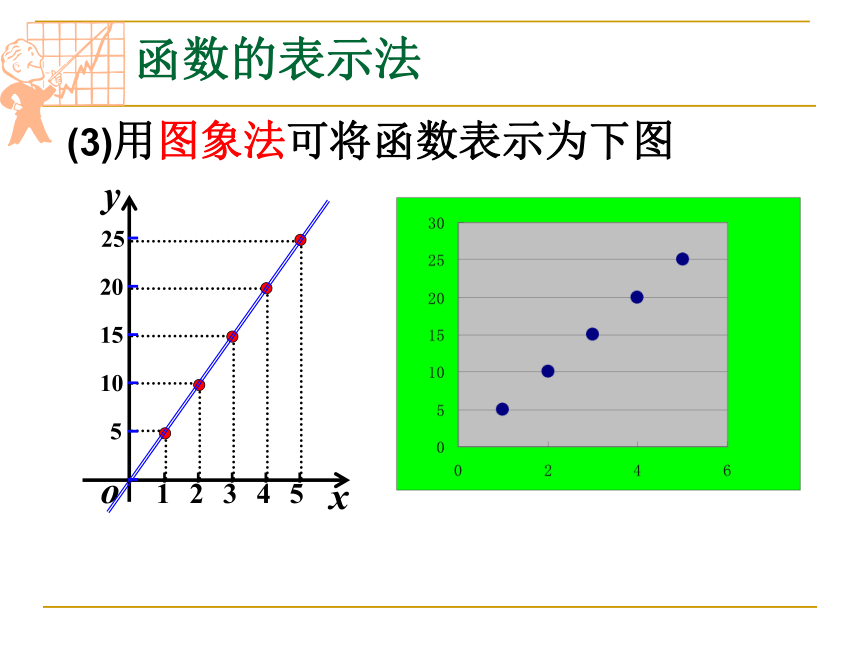
(3)用图象法可将函数表示为下图
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线?
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域.
列表、描点、连线(视其定义域决定是否连线).
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
函数的表示法
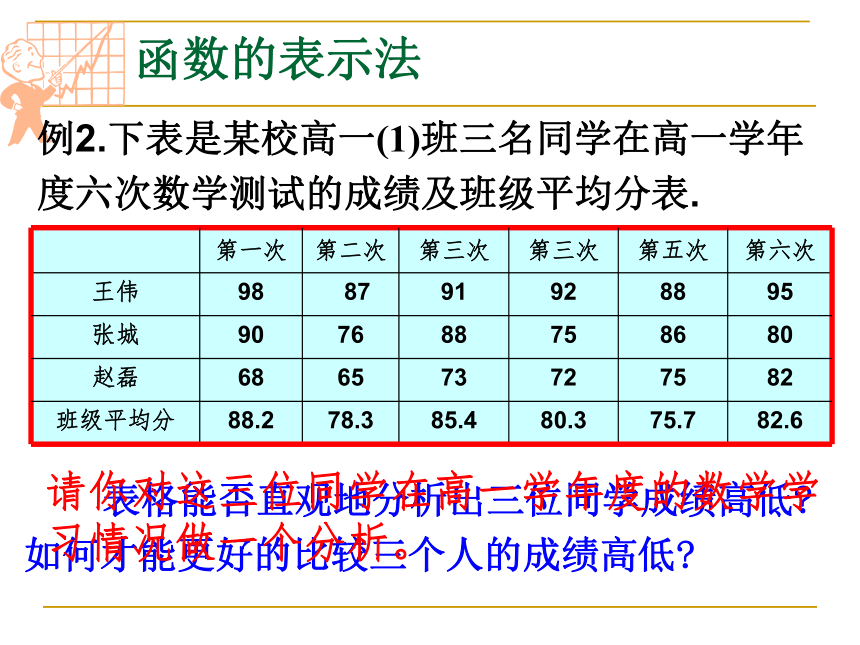
例2.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
表格能否直观地分析出三位同学成绩高低 如何才能更好的比较三个人的成绩高低
请你对这三位同学在高一学年度的数学学习情况做一个分析。
函数的表示法
解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:
王伟同学学习情况稳定且成绩优秀;
张城同学的成绩在班级平均水平上下波动,且波动幅度较大;
赵磊同学的成绩低于班级平均水平,但成绩在稳步提高.
1
2
3
4
5
6
0
60
70
80
90
100
.
.
.
.
.
.
▲
▲
▲
▲
▲
▲
■
■
■
■
■
x
y
王伟
■
张城
班平均分
赵磊
函数的表示法
练习. 向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是( )
B
分段函数
解:由绝对值的意义,知
例3.画出函数 的图象.
图像如下
x
y
o
x
y
o
1
函数图像变换专题
y=| x-1 |
比较例3的做图方法与例1、例2有何不同?
例1、例2采用的是描点法;
例3可借助于已知函数画图象.
描点法一般适用于那些复杂的函数,而对于一些结构比较简单的函数,则通常借助于一些基本函数的图象来变换.
分段函数
例4.某市“招手即停”公共汽车的票价按下列规则制定:
(1) 5公里以内(含5公里),票价2元;
(2) 5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价y与里程x之间的函数解析式,并画出函数的图象.
解:设票价为y元,里程为x公里,由题意可知,自变量的取值范围是(0,20],由票价制定规则,可得到以下函数解析式:
分段函数
解:函数解析式为
y
5
x
10
15
20
1
2
3
4
5
O
有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数.
2,
3,
4,
5,
y
0< x≤5
=
ì
í
5< x≤10
10< x≤15
15< x≤20
分段函数
里程
x(km)
票价
y(元)
2
3
4
5
问:此函数能用列表法表示吗?
此分段函数的定义域为
此分段函数的值域为
③每段上的函数解析式是怎样求出的?
①自变量的范围是怎样得到的?
②自变量的范围为什么分成了四个区间?区间端点是怎样确定的?
作函数图象:
作出下列函数的图象,并求函数的值域:
① y =|1-x|
② y =
x2+1 (x≥0)
-2x (x<0)
③ y = x - n (n∈Z,且-2≤n≤1,x∈[n,n+1))
作函数图象:
① y =|1-x|
①解:y =|1-x|=
函数的值域是 [0,+∞)
x-1 (x≥1)
1-x (x<1)
|x-1|=
x
y
O
4
3
2
1
1
2
3
4
作函数图象:
①解:
函数的值域是(0,+∞)
x
y
O
4
3
2
1
1
2
3
4
② y =
x2+1 (x≥0)
-2x (x<0)
-3
-2
-1
5
分段函数的值域求法:
分别把每段函数的值域求出,再取它们的并集。
作函数图象:
③解:
函数的定义域是[-2,2)
x
y
O
2
1
1
2
-2
-1
③ y = x - n (n∈Z,且-2≤n≤1,x∈[n,n+1)
函数的值域是[0,1)
y =
x+2
∵ n∈Z,且-2≤n≤1
∴ n= -2,-1,0,1
x+1
x
x -1
(n = -2,-2≤x<-1)
(n = -1,-1≤x<0)
(n = 0,0≤x<1)
(n = 1,1≤x<2)
分段函数
注意:
1、有些函数在它的定义域中,对于自变量x的不同取值范围,对应关系不同,这种函数通常称为分段函数。
分段函数的表达式虽然不止一个,但它不是几个函数,而是一个函数。
2、分段函数的定义域是各段“定义域”的并集,
值域是各段“值域”的并集。
3、函数图象不一定是光滑曲线(直线),还可以是一些孤立的点、一些线段、一段曲线等。
分段函数
1. 已知函数
若 f(x)=3, 则x的值是……………( ).
A. 1
B.
C.
D.
D
分段函数是一个函数,不要把它误认为是“几个函数”。
【定义域】?
【值域】?
分段函数
解:由题意知
y = | x + 5 | + | x -1 |
当 x ≤-5 时,
y = -( x + 5 ) -( x -1 )
=-2x-4
当 -5 < x ≤ 1 时,
y = ( x + 5 ) -( x -1 ) = 6
当 x >1 时,
y = ( x + 5 ) + ( x -1 )
= 2x + 4
x
y
o
-5
1
6
2. 化简函数
【定义域】?
【值域】?
分段函数
3. 函数 ,的值域是 。
小结:采取分类的方法,利用已知分段函数,把各段的值域求出来,再取它们的并集;
或把所求函数的值域转化成画函数图象,然后根据函数图象找到函数的值域。
同学们,函数的表示方法有哪几种?你能谈谈它们的优缺点吗?
解析法:即全面地概括了变量之间的依赖关系,又简单明了,便于对函数进行理论上的分析和研究.但有时函数不能用解析法表示,或很难找到这个函数的解析式.
列表法:自变量的值与其对应的函数值一目了然,查找方便.但有很多函数,往往不可能把自变量的所有值与其对应的函数值都列在表中.
图像法:非常直观,可以清楚地看出函数的变化情况.但是,在图像中找对应值时往往不够准确,而且有时函数画不出它的图像,还有很多函数不可能得到它的完整图像.
用适当的方法表示函数,或者把几种方法结合起来,能够帮助我们更好的理解函数和运用函数解决问题
课堂小结
1.理解函数的三种表示法及其各自的优点;
3. 分段函数的表示方法及其图象的画法.
2.通过例1,2,3,掌握描点法和利用已知函数作图的方法、步骤,体会函数的图象(数形结合)在解决数学问题时的直观效果.
作业
补充作业:
求函数y = | 2x+1 | + | x -2 |值域
求函数的解析式
1. y=kx+b经过点(1,0),(0,-1),则y = _______;
2. 求满足下列条件的二次函数 f (x) 的解析式:
顶点坐标为( 2,3 ),且图象经过(3,1)点,
则 f (x) = ________________;
x -1
-2(x-2) 2 + 3
3.已知函数f(x) =x2+x-1,则 f(2)=_____,
若f(x) =5,则 x =_______.
5
2或 -3
求函数的解析式
例1.已知f(x)是一次函数,且f[f(x)]=4x-1, 求f(x)的解析式
解:设 f (x) = kx+b(k≠0)
则 f[f(x)]=f(kx+b)=k(kx+b)+b
=k2x+kb+b=4x-1.
必有
(函数类型确定时用此法)
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
解:
设所求的二次函数为 y=ax2+bx+c (a≠0)
由题意得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程组得:
因此:所求二次函数是:
a=2, b= -3, c=5
y=2x2-3x+5
练习1. 已知一个二次函数的图象过点(-1, 10)、
(1, 4)、(2, 7)三点,求这个函数的解析式?
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
练习2. 已知抛物线的顶点为(-1,-3),与y轴
交点为(0, -5)求抛物线的解析式?
解:
设所求的二次函数为 y=a(x+1)2 - 3 (a≠0)
由条件得:
点( 0, - 5 )在抛物线上
a - 3= - 5, 得a= - 2
故所求的抛物线解析式为 y=-2(x+1)2 - 3
即:y=-2x2-4x-5
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
练习3. 已知抛物线与x轴交于A(-1, 0),B(1, 0),
并经过点M(0, 1),求抛物线的解析式?
解:
设所求的二次函数为 y=a(x+1)(x-1)
由条件得:
点M( 0,1 )在抛物线上
所以:a(0+1)(0-1)=1
得: a= ﹣1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
求函数的解析式
∴ f(x)=x2-1(x≥1).
f(t)=t2 -1
求函数的解析式
解:
设
则
即
练习
求函数的解析式
解:
求函数的解析式
∴ f(x)=x2-1(x≥1).
求函数的解析式
解:
令
则
即
练习
求函数的解析式
——利用方程思想,采用解方程组的方法消去不需要的函数式子
求函数的解析式
求函数的解析式
令 x = 0, y = 0, x = y, x=-y等是常用赋值技巧,具体视题设而定。
求函数的解析式
求函数的解析式
3.1 函数及其表示
3.1.2 函数的表示法
复习回顾
函数的表示法,常用的有三种:
解析法、列表法、图象法。
解析法:把两个变量的函数关系,用一个等式来表示,这个等式叫做函数的解析式。
解析式只表示一种对应关系,与所取的字母无关。
例如:y = 2 x– 1 与 u = 2 t -1 表示同一个函数。
函数解析式一定是方程;
方程不一定是函数解析式。
一次函数:y=kx+b (k≠0)
二次函数:y=ax2+bx+c (a≠0)
可看成关于x、y的方程。
例如:x2+y2=1
复习回顾
(1)炮弹发射
(解析法)
h=130t-5t2 (0≤t≤26)
(2)南极臭氧层空洞
(图象法)
(3)恩格尔系数
(列表法)
时间 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔系数(%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
函数的表示法
1、解析法:用数学表达式表示两个变量之间的对应关系.
解析式
优点:函数关系清楚,容易从自变量的值求出其对应的函数值.便于用解析式来研究函数的性质.
函数的表示法
2、图象法:用图象表示两个变量之间的对应关系.
优点:能直观地表示出函数的变化情况。
注意:图象法是今后利用数形结合思想解题的基础。
图象法:
思考:初中画函数图象主要用什么方法?
利用此法画图的主要步骤如何?
初中画函数图象的主要方法是描点法。
按描点法画函数图象的主要步骤有:
(1)确定自变量 x 的取值范围,对函数图象
的整体性质有个把握;
(2)列表:选取一些典型的点,将x与y的对应值用表列出;
(3)描点:将表中点在直角坐标系中描出;
(4)连线:用平滑直线或曲线依次连接各点。
例如:
一次函数图象:一条直线——两点确定一条直线—
—找两个典型的点——通常找与坐标轴的交点。
二次函数图象:抛物线——开口方向,对称轴,顶
点,与坐标轴交点。
判断一个图形是否是函数图象:
判断下列图象,哪些可以表示函数图象?
x
y
O
x
y
O
x
O
x
O
y
y
A
B
C
D
平行于y轴(也即垂直于x轴)的直线,与函数图象至多有一个交点。
-1
1
函数的表示法
3. 列表法: 列出表格来表示两个变量之间的对应关系.
优点:不必通过运算就知道当自变量取某些值时函数的对应值.
时间(年) 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔
系数(%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
“八五”计划以来我国城镇居民恩格尔系数变化情况
缺点:经常不可能把所有的对应值列入数表中,而只能达到实际上够用的程度。
函数的表示法
解:(1)用解析法可将函数y=f(x)表示为
y=5x,
(2)用列表法可将函数表示为
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
例1、某种笔记本的单价是5元,买x (x∈{1,2,3,4,5}) 个笔记本需要 y 元.试用函数的三种表示法表示函数y=f(x).
函数的表示法
x
y
o
5
10
15
20
25
1
2
3
4
5
(3)用图象法可将函数表示为下图
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线?
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域.
列表、描点、连线(视其定义域决定是否连线).
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
函数的表示法
例2.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
表格能否直观地分析出三位同学成绩高低 如何才能更好的比较三个人的成绩高低
请你对这三位同学在高一学年度的数学学习情况做一个分析。
函数的表示法
解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:
王伟同学学习情况稳定且成绩优秀;
张城同学的成绩在班级平均水平上下波动,且波动幅度较大;
赵磊同学的成绩低于班级平均水平,但成绩在稳步提高.
1
2
3
4
5
6
0
60
70
80
90
100
.
.
.
.
.
.
▲
▲
▲
▲
▲
▲
■
■
■
■
■
x
y
王伟
■
张城
班平均分
赵磊
函数的表示法
练习. 向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是( )
B
分段函数
解:由绝对值的意义,知
例3.画出函数 的图象.
图像如下
x
y
o
x
y
o
1
函数图像变换专题
y=| x-1 |
比较例3的做图方法与例1、例2有何不同?
例1、例2采用的是描点法;
例3可借助于已知函数画图象.
描点法一般适用于那些复杂的函数,而对于一些结构比较简单的函数,则通常借助于一些基本函数的图象来变换.
分段函数
例4.某市“招手即停”公共汽车的票价按下列规则制定:
(1) 5公里以内(含5公里),票价2元;
(2) 5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价y与里程x之间的函数解析式,并画出函数的图象.
解:设票价为y元,里程为x公里,由题意可知,自变量的取值范围是(0,20],由票价制定规则,可得到以下函数解析式:
分段函数
解:函数解析式为
y
5
x
10
15
20
1
2
3
4
5
O
有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数.
2,
3,
4,
5,
y
0< x≤5
=
ì
í
5< x≤10
10< x≤15
15< x≤20
分段函数
里程
x(km)
票价
y(元)
2
3
4
5
问:此函数能用列表法表示吗?
此分段函数的定义域为
此分段函数的值域为
③每段上的函数解析式是怎样求出的?
①自变量的范围是怎样得到的?
②自变量的范围为什么分成了四个区间?区间端点是怎样确定的?
作函数图象:
作出下列函数的图象,并求函数的值域:
① y =|1-x|
② y =
x2+1 (x≥0)
-2x (x<0)
③ y = x - n (n∈Z,且-2≤n≤1,x∈[n,n+1))
作函数图象:
① y =|1-x|
①解:y =|1-x|=
函数的值域是 [0,+∞)
x-1 (x≥1)
1-x (x<1)
|x-1|=
x
y
O
4
3
2
1
1
2
3
4
作函数图象:
①解:
函数的值域是(0,+∞)
x
y
O
4
3
2
1
1
2
3
4
② y =
x2+1 (x≥0)
-2x (x<0)
-3
-2
-1
5
分段函数的值域求法:
分别把每段函数的值域求出,再取它们的并集。
作函数图象:
③解:
函数的定义域是[-2,2)
x
y
O
2
1
1
2
-2
-1
③ y = x - n (n∈Z,且-2≤n≤1,x∈[n,n+1)
函数的值域是[0,1)
y =
x+2
∵ n∈Z,且-2≤n≤1
∴ n= -2,-1,0,1
x+1
x
x -1
(n = -2,-2≤x<-1)
(n = -1,-1≤x<0)
(n = 0,0≤x<1)
(n = 1,1≤x<2)
分段函数
注意:
1、有些函数在它的定义域中,对于自变量x的不同取值范围,对应关系不同,这种函数通常称为分段函数。
分段函数的表达式虽然不止一个,但它不是几个函数,而是一个函数。
2、分段函数的定义域是各段“定义域”的并集,
值域是各段“值域”的并集。
3、函数图象不一定是光滑曲线(直线),还可以是一些孤立的点、一些线段、一段曲线等。
分段函数
1. 已知函数
若 f(x)=3, 则x的值是……………( ).
A. 1
B.
C.
D.
D
分段函数是一个函数,不要把它误认为是“几个函数”。
【定义域】?
【值域】?
分段函数
解:由题意知
y = | x + 5 | + | x -1 |
当 x ≤-5 时,
y = -( x + 5 ) -( x -1 )
=-2x-4
当 -5 < x ≤ 1 时,
y = ( x + 5 ) -( x -1 ) = 6
当 x >1 时,
y = ( x + 5 ) + ( x -1 )
= 2x + 4
x
y
o
-5
1
6
2. 化简函数
【定义域】?
【值域】?
分段函数
3. 函数 ,的值域是 。
小结:采取分类的方法,利用已知分段函数,把各段的值域求出来,再取它们的并集;
或把所求函数的值域转化成画函数图象,然后根据函数图象找到函数的值域。
同学们,函数的表示方法有哪几种?你能谈谈它们的优缺点吗?
解析法:即全面地概括了变量之间的依赖关系,又简单明了,便于对函数进行理论上的分析和研究.但有时函数不能用解析法表示,或很难找到这个函数的解析式.
列表法:自变量的值与其对应的函数值一目了然,查找方便.但有很多函数,往往不可能把自变量的所有值与其对应的函数值都列在表中.
图像法:非常直观,可以清楚地看出函数的变化情况.但是,在图像中找对应值时往往不够准确,而且有时函数画不出它的图像,还有很多函数不可能得到它的完整图像.
用适当的方法表示函数,或者把几种方法结合起来,能够帮助我们更好的理解函数和运用函数解决问题
课堂小结
1.理解函数的三种表示法及其各自的优点;
3. 分段函数的表示方法及其图象的画法.
2.通过例1,2,3,掌握描点法和利用已知函数作图的方法、步骤,体会函数的图象(数形结合)在解决数学问题时的直观效果.
作业
补充作业:
求函数y = | 2x+1 | + | x -2 |值域
求函数的解析式
1. y=kx+b经过点(1,0),(0,-1),则y = _______;
2. 求满足下列条件的二次函数 f (x) 的解析式:
顶点坐标为( 2,3 ),且图象经过(3,1)点,
则 f (x) = ________________;
x -1
-2(x-2) 2 + 3
3.已知函数f(x) =x2+x-1,则 f(2)=_____,
若f(x) =5,则 x =_______.
5
2或 -3
求函数的解析式
例1.已知f(x)是一次函数,且f[f(x)]=4x-1, 求f(x)的解析式
解:设 f (x) = kx+b(k≠0)
则 f[f(x)]=f(kx+b)=k(kx+b)+b
=k2x+kb+b=4x-1.
必有
(函数类型确定时用此法)
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
解:
设所求的二次函数为 y=ax2+bx+c (a≠0)
由题意得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程组得:
因此:所求二次函数是:
a=2, b= -3, c=5
y=2x2-3x+5
练习1. 已知一个二次函数的图象过点(-1, 10)、
(1, 4)、(2, 7)三点,求这个函数的解析式?
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
练习2. 已知抛物线的顶点为(-1,-3),与y轴
交点为(0, -5)求抛物线的解析式?
解:
设所求的二次函数为 y=a(x+1)2 - 3 (a≠0)
由条件得:
点( 0, - 5 )在抛物线上
a - 3= - 5, 得a= - 2
故所求的抛物线解析式为 y=-2(x+1)2 - 3
即:y=-2x2-4x-5
求函数的解析式
一般式: y=ax2+bx+c (a≠0)
两根式:
y=a(x-x1)(x-x2) (a≠0)
顶点式:
y=a(x-h)2+k (a≠0)
练习3. 已知抛物线与x轴交于A(-1, 0),B(1, 0),
并经过点M(0, 1),求抛物线的解析式?
解:
设所求的二次函数为 y=a(x+1)(x-1)
由条件得:
点M( 0,1 )在抛物线上
所以:a(0+1)(0-1)=1
得: a= ﹣1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
求函数的解析式
∴ f(x)=x2-1(x≥1).
f(t)=t2 -1
求函数的解析式
解:
设
则
即
练习
求函数的解析式
解:
求函数的解析式
∴ f(x)=x2-1(x≥1).
求函数的解析式
解:
令
则
即
练习
求函数的解析式
——利用方程思想,采用解方程组的方法消去不需要的函数式子
求函数的解析式
求函数的解析式
令 x = 0, y = 0, x = y, x=-y等是常用赋值技巧,具体视题设而定。
求函数的解析式
求函数的解析式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
