2013届中考冲刺:历届原题精选【求一次函数的解析式及一次函数的应用】解答题模块(含详解)
文档属性
| 名称 | 2013届中考冲刺:历届原题精选【求一次函数的解析式及一次函数的应用】解答题模块(含详解) |  | |
| 格式 | zip | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-12 16:07:32 | ||
图片预览


文档简介
【求一次函数的解析式及一次函数的应用】
中考考试原题精选
1、星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了_________米3的天然气;
(2)当x≧8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气_________米3,这第20辆车在当天9:00之前能加完气吗?请说明理由.
解:(1)根据图象可得出:燃气公司向储气罐注入了10000﹣2000=8000(米3)的天然气;故答案为:8000;
(2)当x≧8.5时由图象可设y与x的函数关系式为y=kx+b,
由已知得:,
解得,
故当x≧8.5时,储气罐中的储气量y(米3)与时间x(小时)的函数关系式为:y=﹣1000x+18500,
(3)根据每车20米3的加气量,则20辆车加完气后,储气罐内还有天然气:10000﹣20×20=9600(米3),
故答案为:9600,
根据题意得出:
9600=﹣1000x+18500,x=8.9<9,:
这第20辆车在当天9:00之前能加完气.
2、如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).
(1)求G点坐标;
(2)求直线EF解析式;
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
解:(1)由已知得,FG=AF=2,FB=1
∵四边形ABCD为矩形
∴∠B=90°BG===
∴G点的坐标为(3,4﹣);
(2)设直线EF的解析式是y=kx+b在Rt△BFG中,cos∠BFG==
∴∠BFG=60°
∴∠AFE=∠EFG=60°
∴AE=AFtan∠AFE=2tan60°=2
∴E点的坐标为(0,4﹣2)
又F点的坐标是(2,4)
∴
解得k=,b=4﹣2;
∴直线EF的解析式为y=x+4﹣2;
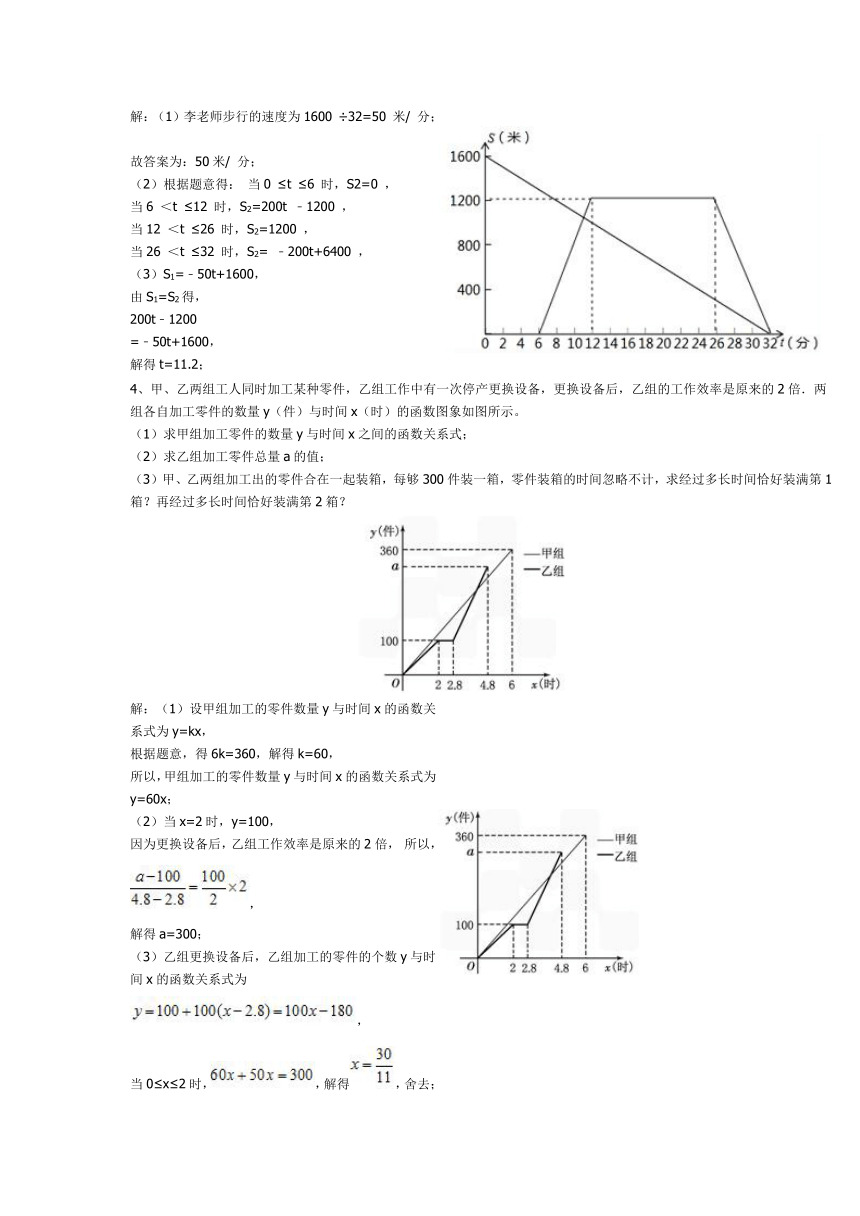
3、张勤同学的父母在外打工,家中只有年迈多病的奶奶,星期天早上,李老师从家中出发步行前往张勤家家访,6 分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14 分钟后以相同的速度按原路返回,结果与李老师同时到家,张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t (0 ≤t ≤32 )分钟后师生二人离张勤家的距离分别为S1、S2,S 与t 之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为_______;
(2)求S2与t 之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
解:(1)李老师步行的速度为1600 ÷32=50 米/ 分;
故答案为:50米/ 分;
(2)根据题意得: 当0 ≤t ≤6 时,S2=0 ,
当6 <t ≤12 时,S2=200t ﹣1200 ,
当12 <t ≤26 时,S2=1200 ,
当26 <t ≤32 时,S2= ﹣200t+6400 ,
(3)S1=﹣50t+1600,
由S1=S2得,
200t﹣1200
=﹣50t+1600,
解得t=11.2;
4、甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示。
(1)求甲组加工零件的数量y与时间x之间的函数关系式;
(2)求乙组加工零件总量a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
解:(1)设甲组加工的零件数量y与时间x的函数关系式为y=kx,
根据题意,得6k=360,解得k=60,
所以,甲组加工的零件数量y与时间x的函数关系式为y=60x;
(2)当x=2时,y=100,
因为更换设备后,乙组工作效率是原来的2倍, 所以,,
解得a=300;
(3)乙组更换设备后,乙组加工的零件的个数y与时间x的函数关系式为,
当0≤x≤2时,,解得,舍去;
当2当2.8所以,经过3小时恰好装满第1箱,
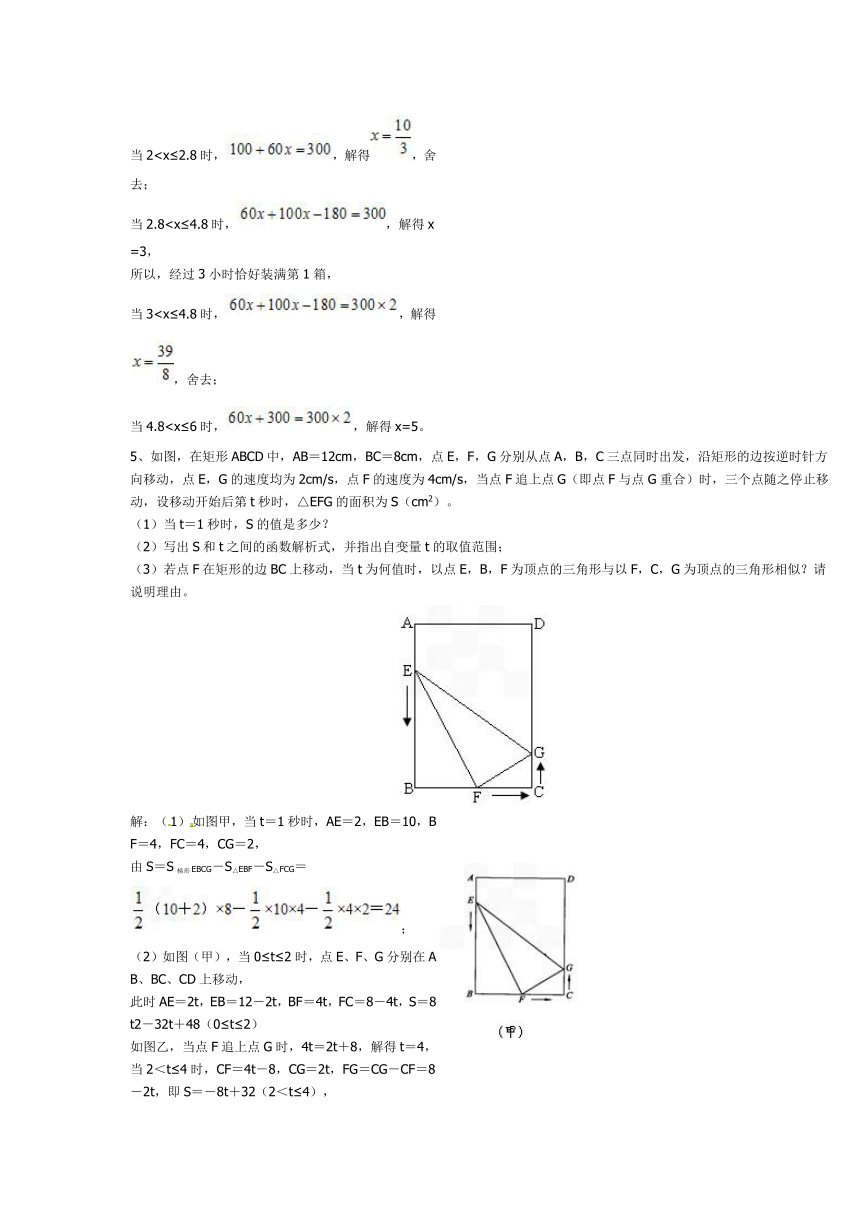
当3当4.85、如图,在矩形ABCD中,AB=12cm,BC=8cm,点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动,设移动开始后第t秒时,△EFG的面积为S(cm2)。
(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由。
解:(1)如图甲,当t=1秒时,AE=2,EB=10,BF=4,FC=4,CG=2,
由S=S梯形EBCG-S△EBF-S△FCG=;
(2)如图(甲),当0≤t≤2时,点E、F、G分别在AB、BC、CD上移动,
此时AE=2t,EB=12-2t,BF=4t,FC=8-4t,S=8t2-32t+48(0≤t≤2)
如图乙,当点F追上点G时,4t=2t+8,解得t=4,
当2<t≤4时,CF=4t-8,CG=2t,FG=CG-CF=8-2t,即S=-8t+32(2<t≤4),
(3)如图(甲),当点F在矩形的边BC上移动时,0≤t≤2,
在△EBF和△FCG中,∠B=∠C=90o,
①若,即,解得t=,又t=满足0≤t≤2,所以当t=时△EBF∽△FCG;
②若,即,解得t=,又t=满足0≤t≤2,所以当t=时△EBF∽△GCF,
综上知,当t=或时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似。
6、直线与反比例函数(x>0)的图像交于点A,与坐标轴分别交于M、N两点,当AM=MN时,求k的值。
解:过点A作AB⊥x轴, 垂足为B,对于直线y=kx+
当x=0 时,
即OM=
∵AM=MN
∴AN=2MN
∵Rt △MON∽Rt △ABN
∴
∴
将代入中得 x=1
∴A(1,)
∵点A在直线y=kx+上
∴= k+
∴k=。
7、某超市销售一种新鲜“酸奶”, 此“酸奶”以每瓶3 元购进,5 元售出. 这种“酸奶”的保质期不超过一天,对当天未售出的“酸奶”必须全部做销毁处理。
(1)该超市某一天购进20 瓶酸奶进行销售,若设售出酸奶的瓶数为x (瓶),销售酸奶的利润为y (元),写出这一天销售酸奶的利润y (元)与售出的瓶数x (瓶)之间的函数关系式. 为确保超市在销售这20 瓶酸奶时不亏本,当天至少应售出多少瓶?
(2)小明在社会调查活动中,了解到近10 天当中,该超市每天购进酸奶20 瓶的销售情况统计如下:
根据上表,求该超市这10 天每天销售酸奶的利润的平均数;
(3)小明根据(2)中,10天酸奶的销售情况统计,计算得出在近10天当中,其实每天购进19 瓶总获利要比每天购进20 瓶总获利还多. 你认为小明的说法有道理吗?试通过计算说明。
解(1)由题意知,这一天销售酸奶的利润y (元)与售出的瓶数x (瓶)之间的函数关系式为:y=5x-60,
当5x-60 ≥0 时,x ≥12
∴当天至少应售出12 瓶酸奶超市才不亏本;
(2)在这10 天当中,利润为25 元的有1 天,30元的有2 天,35 元的有2 天,40 元的有5 天
∴这10 天中,每天销售酸奶的利润的平均数为(25+30 ×2+35 ×2+40 ×5 )÷10=35.5;
(3)小明说的有道理,
∵在这10 天当中, 每天购进20 瓶获利共计355元,而每天购进19 瓶销售酸奶的利润y(元)与售出的瓶数x (瓶)之间的函数关系式为:y=5x-57,
在10天当中,利润为28元的有1天,33元的有2天,38元的有7天,
总获利为28+33×2+38×7=360>355
∴小明说的有道理。
8、已知抛物线经过A(2,0),设顶点为点P,与x轴的另一交点为点B。
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由。
解:(1)由于抛物线经过A(2,0),
所以,
解得
所以抛物线的解析式为,
(*)将(*)配方,得,
所以顶点P的坐标为(4,-2),
令y=0,得,解得,
所以点B的坐标是(6,0);
(2)在直线上存在点D,使四边形OPBD为平行四边形,
理由如下:设直线PB的解析式为y=kx+b,把B(6,0),P(4,-2)分别代入,
得,解得
所以直线PB的解析式为,
又直线OD的解析式为
所以直线PB∥OD,
设设直线OP的解析式为y=mx,
把P(4,-2)代入,得 解得,
如果OP∥BD,那么四边形OPBD为平行四边形,
设直线BD的解析式为,将B(6,0)代入,得0=,
所以,
所以直线BD的解析式为,
解方程组,得
所以D点的坐标为(2,2);
(3)符合条件的点M存在.验证如下:
过点P作x轴的垂线,垂足为为C,则PC=2,AC=2,
由勾股定理,可得AP=4,PB=4,又AB=4,
所以△APB是等边三角形,只要作∠PAB的平分线交抛物线于M点,
连接PM,BM,
由于AM=AM,∠PAM=∠BAM,AB=AP,
可得△AMP≌△AMB,
因此即存在这样的点M,使△AMP≌△AMB。
9、将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数解析式可以是( )(写出一个即可)。
y=-6x+1(答案不惟一)
10、某仓库有甲种货物360吨,乙种货物290吨,计划用A、B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为x辆,运输这批货物的总运费为y万元,试写出y与x的关系表达式;
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案?请设计出来;
(3)试说明哪种方案总运费最少?最少运费是多少万元?
解:(1)设A种货车为x辆,则B种货车为(50-x)辆.
根据题意,得
(2)根据题意,得
解这个不等式组,得.
∵x是整数,
∴x可取20、21、22
(3)由(1)可知,总运费
∵k=-0.3<0,
∴一次函数的函数值随x的增大而减小.
所以时,y有最小值.即
选择方案三:A种货车为22辆,B种货车为28辆,总运费最少是33.4万元.
中考考试原题精选
1、星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了_________米3的天然气;
(2)当x≧8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气_________米3,这第20辆车在当天9:00之前能加完气吗?请说明理由.
解:(1)根据图象可得出:燃气公司向储气罐注入了10000﹣2000=8000(米3)的天然气;故答案为:8000;
(2)当x≧8.5时由图象可设y与x的函数关系式为y=kx+b,
由已知得:,
解得,
故当x≧8.5时,储气罐中的储气量y(米3)与时间x(小时)的函数关系式为:y=﹣1000x+18500,
(3)根据每车20米3的加气量,则20辆车加完气后,储气罐内还有天然气:10000﹣20×20=9600(米3),
故答案为:9600,
根据题意得出:
9600=﹣1000x+18500,x=8.9<9,:
这第20辆车在当天9:00之前能加完气.
2、如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).
(1)求G点坐标;
(2)求直线EF解析式;
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
解:(1)由已知得,FG=AF=2,FB=1
∵四边形ABCD为矩形
∴∠B=90°BG===
∴G点的坐标为(3,4﹣);
(2)设直线EF的解析式是y=kx+b在Rt△BFG中,cos∠BFG==
∴∠BFG=60°
∴∠AFE=∠EFG=60°
∴AE=AFtan∠AFE=2tan60°=2
∴E点的坐标为(0,4﹣2)
又F点的坐标是(2,4)
∴
解得k=,b=4﹣2;
∴直线EF的解析式为y=x+4﹣2;
3、张勤同学的父母在外打工,家中只有年迈多病的奶奶,星期天早上,李老师从家中出发步行前往张勤家家访,6 分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14 分钟后以相同的速度按原路返回,结果与李老师同时到家,张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t (0 ≤t ≤32 )分钟后师生二人离张勤家的距离分别为S1、S2,S 与t 之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为_______;
(2)求S2与t 之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
解:(1)李老师步行的速度为1600 ÷32=50 米/ 分;
故答案为:50米/ 分;
(2)根据题意得: 当0 ≤t ≤6 时,S2=0 ,
当6 <t ≤12 时,S2=200t ﹣1200 ,
当12 <t ≤26 时,S2=1200 ,
当26 <t ≤32 时,S2= ﹣200t+6400 ,
(3)S1=﹣50t+1600,
由S1=S2得,
200t﹣1200
=﹣50t+1600,
解得t=11.2;
4、甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示。
(1)求甲组加工零件的数量y与时间x之间的函数关系式;
(2)求乙组加工零件总量a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
解:(1)设甲组加工的零件数量y与时间x的函数关系式为y=kx,
根据题意,得6k=360,解得k=60,
所以,甲组加工的零件数量y与时间x的函数关系式为y=60x;
(2)当x=2时,y=100,
因为更换设备后,乙组工作效率是原来的2倍, 所以,,
解得a=300;
(3)乙组更换设备后,乙组加工的零件的个数y与时间x的函数关系式为,
当0≤x≤2时,,解得,舍去;
当2
当3
(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由。
解:(1)如图甲,当t=1秒时,AE=2,EB=10,BF=4,FC=4,CG=2,
由S=S梯形EBCG-S△EBF-S△FCG=;
(2)如图(甲),当0≤t≤2时,点E、F、G分别在AB、BC、CD上移动,
此时AE=2t,EB=12-2t,BF=4t,FC=8-4t,S=8t2-32t+48(0≤t≤2)
如图乙,当点F追上点G时,4t=2t+8,解得t=4,
当2<t≤4时,CF=4t-8,CG=2t,FG=CG-CF=8-2t,即S=-8t+32(2<t≤4),
(3)如图(甲),当点F在矩形的边BC上移动时,0≤t≤2,
在△EBF和△FCG中,∠B=∠C=90o,
①若,即,解得t=,又t=满足0≤t≤2,所以当t=时△EBF∽△FCG;
②若,即,解得t=,又t=满足0≤t≤2,所以当t=时△EBF∽△GCF,
综上知,当t=或时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似。
6、直线与反比例函数(x>0)的图像交于点A,与坐标轴分别交于M、N两点,当AM=MN时,求k的值。
解:过点A作AB⊥x轴, 垂足为B,对于直线y=kx+
当x=0 时,
即OM=
∵AM=MN
∴AN=2MN
∵Rt △MON∽Rt △ABN
∴
∴
将代入中得 x=1
∴A(1,)
∵点A在直线y=kx+上
∴= k+
∴k=。
7、某超市销售一种新鲜“酸奶”, 此“酸奶”以每瓶3 元购进,5 元售出. 这种“酸奶”的保质期不超过一天,对当天未售出的“酸奶”必须全部做销毁处理。
(1)该超市某一天购进20 瓶酸奶进行销售,若设售出酸奶的瓶数为x (瓶),销售酸奶的利润为y (元),写出这一天销售酸奶的利润y (元)与售出的瓶数x (瓶)之间的函数关系式. 为确保超市在销售这20 瓶酸奶时不亏本,当天至少应售出多少瓶?
(2)小明在社会调查活动中,了解到近10 天当中,该超市每天购进酸奶20 瓶的销售情况统计如下:
根据上表,求该超市这10 天每天销售酸奶的利润的平均数;
(3)小明根据(2)中,10天酸奶的销售情况统计,计算得出在近10天当中,其实每天购进19 瓶总获利要比每天购进20 瓶总获利还多. 你认为小明的说法有道理吗?试通过计算说明。
解(1)由题意知,这一天销售酸奶的利润y (元)与售出的瓶数x (瓶)之间的函数关系式为:y=5x-60,
当5x-60 ≥0 时,x ≥12
∴当天至少应售出12 瓶酸奶超市才不亏本;
(2)在这10 天当中,利润为25 元的有1 天,30元的有2 天,35 元的有2 天,40 元的有5 天
∴这10 天中,每天销售酸奶的利润的平均数为(25+30 ×2+35 ×2+40 ×5 )÷10=35.5;
(3)小明说的有道理,
∵在这10 天当中, 每天购进20 瓶获利共计355元,而每天购进19 瓶销售酸奶的利润y(元)与售出的瓶数x (瓶)之间的函数关系式为:y=5x-57,
在10天当中,利润为28元的有1天,33元的有2天,38元的有7天,
总获利为28+33×2+38×7=360>355
∴小明说的有道理。
8、已知抛物线经过A(2,0),设顶点为点P,与x轴的另一交点为点B。
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由。
解:(1)由于抛物线经过A(2,0),
所以,
解得
所以抛物线的解析式为,
(*)将(*)配方,得,
所以顶点P的坐标为(4,-2),
令y=0,得,解得,
所以点B的坐标是(6,0);
(2)在直线上存在点D,使四边形OPBD为平行四边形,
理由如下:设直线PB的解析式为y=kx+b,把B(6,0),P(4,-2)分别代入,
得,解得
所以直线PB的解析式为,
又直线OD的解析式为
所以直线PB∥OD,
设设直线OP的解析式为y=mx,
把P(4,-2)代入,得 解得,
如果OP∥BD,那么四边形OPBD为平行四边形,
设直线BD的解析式为,将B(6,0)代入,得0=,
所以,
所以直线BD的解析式为,
解方程组,得
所以D点的坐标为(2,2);
(3)符合条件的点M存在.验证如下:
过点P作x轴的垂线,垂足为为C,则PC=2,AC=2,
由勾股定理,可得AP=4,PB=4,又AB=4,
所以△APB是等边三角形,只要作∠PAB的平分线交抛物线于M点,
连接PM,BM,
由于AM=AM,∠PAM=∠BAM,AB=AP,
可得△AMP≌△AMB,
因此即存在这样的点M,使△AMP≌△AMB。
9、将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数解析式可以是( )(写出一个即可)。
y=-6x+1(答案不惟一)
10、某仓库有甲种货物360吨,乙种货物290吨,计划用A、B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为x辆,运输这批货物的总运费为y万元,试写出y与x的关系表达式;
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案?请设计出来;
(3)试说明哪种方案总运费最少?最少运费是多少万元?
解:(1)设A种货车为x辆,则B种货车为(50-x)辆.
根据题意,得
(2)根据题意,得
解这个不等式组,得.
∵x是整数,
∴x可取20、21、22
(3)由(1)可知,总运费
∵k=-0.3<0,
∴一次函数的函数值随x的增大而减小.
所以时,y有最小值.即
选择方案三:A种货车为22辆,B种货车为28辆,总运费最少是33.4万元.
同课章节目录
