解三角形
图片预览


文档简介
解三角形单元测试题
一、选择题:
1. △ABC中,sin2A=sin2B+sin2C,则△ABC为( )?
A直角三角形? B等腰直角三角形?C等边三角形 D等腰三角形
2. 在△ABC中,b=,c=3,B=300,则a等于( )
A. B.12 C.或2 D.2
3. 已知△ABC的周长为9,且,则cosC的值为 ( )
A. B. C. D.
4. 在△ABC中,A=60°,b=1,其面积为,则等于( )
A.3 B. C. D.
5. 在△ABC中,AB=5,BC=7,AC=8,则的值为( )
A.79 B.69 C.5 D.-5
6.关于x的方程有一个根为1,则△ABC一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
7. 设m、m+1、m+2是钝角三角形的三边长,则实数m的取值范围是( )
A.0<m<3 B.1<m<3 C.3<m<4 D.4<m<6
8. △ABC中,若c=,则角C的度数是( )
A.60° B.120° C.60°或120° D.45°
9.在△ABC中,,那么△ABC一定是 ( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.等腰三角形或直角三角形
10. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定
二、填空题
13.在△ABC中,有等式:①asinA=bsinB;②asinB=bsinA;③acosB=bcosA;④. 其中恒成立的等式序号为______________
14. 在等腰三角形 ABC中,已知sinA∶sinB=1∶2,底边BC=10,则△ABC的周长是 。
15. 在△ABC中,已知sinA∶sinB∶sinC=3∶5∶7,则此三角形的最大内角的度数等于________.
16. 已知△ABC的三边分别是a、b、c,且面积,则角C=____________.
三、解答题
17. 已知在△ABC中,A=450,AB=,BC=2,求解此三角形.
18. 在△ABC中,已知a-b=4,a+c=2b,且最大角为120°,求△ABC的三边长.
19. 在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积.
20. 在△ABC中,已知边c=10, 又知==,求a、b。
21.在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。
22.如图,测量河对岸的塔高时,可以选与塔底在
同一水平面内的两个测点与,测得,
,米,并在点测得塔顶的
仰角为,求塔高
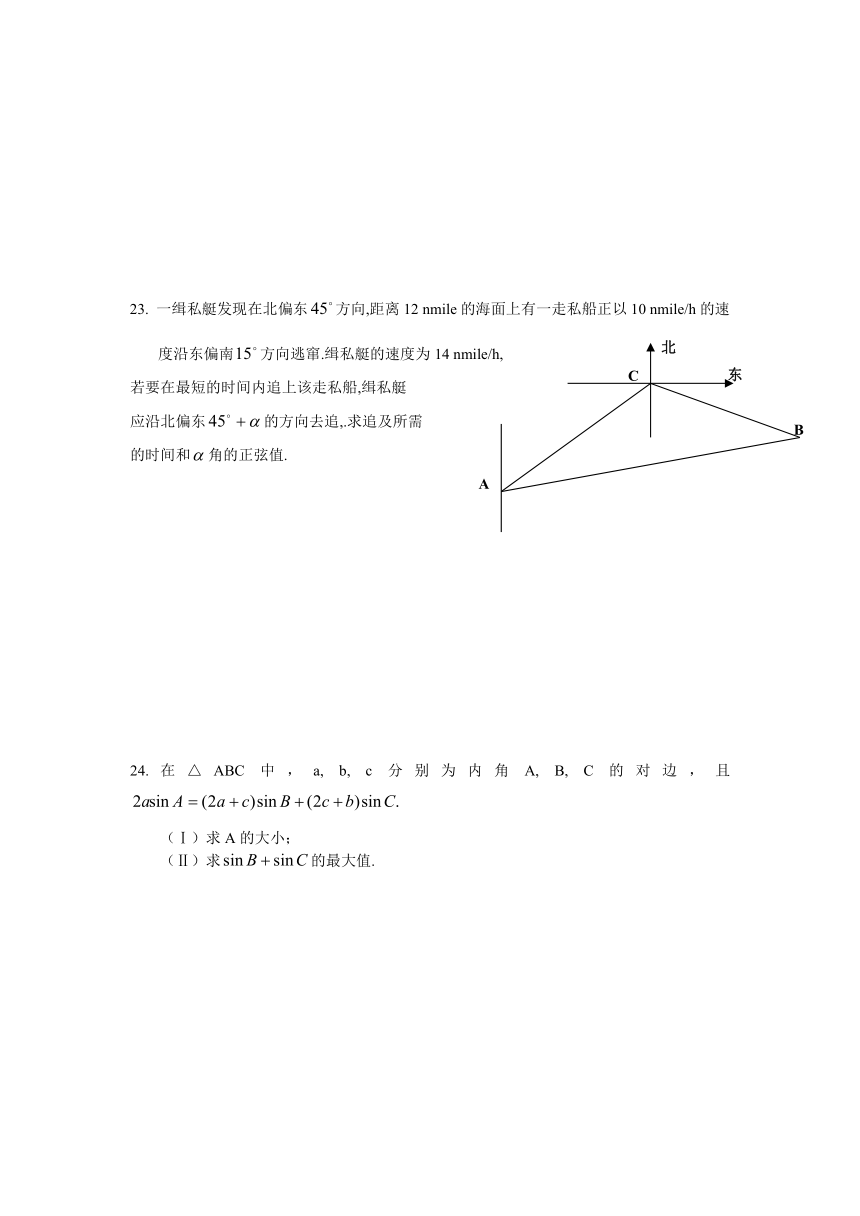
23. 一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h,
若要在最短的时间内追上该走私船,缉私艇
应沿北偏东的方向去追,.求追及所需
的时间和角的正弦值.
24.在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
25.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南方向300km的海面P处,并以20km/h的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
正余弦定理单元测试参考答案
A 2.C 3. A 4. B 5. D 6. A 7. B 8.B 9.D 10.A
13. ②④ 14.50, 15.1200,16. 450
17. 解答:C=120 B=15 AC=或C=60 B=75
18. 解答:a=14,b=10,c=6
19. 解答:解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, S△ABC=absinC=×2×= .
20.解答:由=,=,可得 =,变形为sinAcosA=sinBcosB
∴sin2A=sin2B, 又∵a≠b, ∴2A=π-2B, ∴A+B=. ∴△ABC为直角三角形.
由a2+b2=102和=,解得a=6, b=8,
21. 解答:由tanA+tanB=tanA·tanB-可得=-,即tan(A+B)=-
∴tan(π-C)= -, ∴-tanC=-, ∴tanC=∵C∈(0, π), ∴C=又△ABC的面积为S△ABC=,∴absinC=即ab×=, ∴ab=6又由余弦定理可得c2=a2+b2-2abcosC
∴()2= a2+b2-2abcos∴()2= a2+b2-ab=(a+b)2-3ab∴(a+b)2=, ∵a+b>0, ∴a+b=
23.解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, 则有
,
所以所需时间2小时,
24.解:(Ⅰ)由已知,根据正弦定理得
即 由余弦定理得
故 ,A=120°
(Ⅱ)由(Ⅰ)得:
故当B=30°时,sinB+sinC取得最大值1。
25.解:设在t时刻台风中心位于点Q,此时|OP|=300,|PQ|=20t,
台风侵袭范围的圆形区域半径为r(t)=10t+60,
由,可知,
cos∠OPQ=cos(θ-45o)= cosθcos45o+ sinθsin45o
=
在 △OPQ中,由余弦定理,得
=
=
若城市O受到台风的侵袭,则有|OQ|≤r(t),即
,
整理,得,解得12≤t≤24,
答:12小时后该城市开始受到台风的侵袭.
一、选择题:
1. △ABC中,sin2A=sin2B+sin2C,则△ABC为( )?
A直角三角形? B等腰直角三角形?C等边三角形 D等腰三角形
2. 在△ABC中,b=,c=3,B=300,则a等于( )
A. B.12 C.或2 D.2
3. 已知△ABC的周长为9,且,则cosC的值为 ( )
A. B. C. D.
4. 在△ABC中,A=60°,b=1,其面积为,则等于( )
A.3 B. C. D.
5. 在△ABC中,AB=5,BC=7,AC=8,则的值为( )
A.79 B.69 C.5 D.-5
6.关于x的方程有一个根为1,则△ABC一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
7. 设m、m+1、m+2是钝角三角形的三边长,则实数m的取值范围是( )
A.0<m<3 B.1<m<3 C.3<m<4 D.4<m<6
8. △ABC中,若c=,则角C的度数是( )
A.60° B.120° C.60°或120° D.45°
9.在△ABC中,,那么△ABC一定是 ( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.等腰三角形或直角三角形
10. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定
二、填空题
13.在△ABC中,有等式:①asinA=bsinB;②asinB=bsinA;③acosB=bcosA;④. 其中恒成立的等式序号为______________
14. 在等腰三角形 ABC中,已知sinA∶sinB=1∶2,底边BC=10,则△ABC的周长是 。
15. 在△ABC中,已知sinA∶sinB∶sinC=3∶5∶7,则此三角形的最大内角的度数等于________.
16. 已知△ABC的三边分别是a、b、c,且面积,则角C=____________.
三、解答题
17. 已知在△ABC中,A=450,AB=,BC=2,求解此三角形.
18. 在△ABC中,已知a-b=4,a+c=2b,且最大角为120°,求△ABC的三边长.
19. 在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积.
20. 在△ABC中,已知边c=10, 又知==,求a、b。
21.在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。
22.如图,测量河对岸的塔高时,可以选与塔底在
同一水平面内的两个测点与,测得,
,米,并在点测得塔顶的
仰角为,求塔高
23. 一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h,
若要在最短的时间内追上该走私船,缉私艇
应沿北偏东的方向去追,.求追及所需
的时间和角的正弦值.
24.在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
25.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南方向300km的海面P处,并以20km/h的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
正余弦定理单元测试参考答案
A 2.C 3. A 4. B 5. D 6. A 7. B 8.B 9.D 10.A
13. ②④ 14.50, 15.1200,16. 450
17. 解答:C=120 B=15 AC=或C=60 B=75
18. 解答:a=14,b=10,c=6
19. 解答:解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, S△ABC=absinC=×2×= .
20.解答:由=,=,可得 =,变形为sinAcosA=sinBcosB
∴sin2A=sin2B, 又∵a≠b, ∴2A=π-2B, ∴A+B=. ∴△ABC为直角三角形.
由a2+b2=102和=,解得a=6, b=8,
21. 解答:由tanA+tanB=tanA·tanB-可得=-,即tan(A+B)=-
∴tan(π-C)= -, ∴-tanC=-, ∴tanC=∵C∈(0, π), ∴C=又△ABC的面积为S△ABC=,∴absinC=即ab×=, ∴ab=6又由余弦定理可得c2=a2+b2-2abcosC
∴()2= a2+b2-2abcos∴()2= a2+b2-ab=(a+b)2-3ab∴(a+b)2=, ∵a+b>0, ∴a+b=
23.解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, 则有
,
所以所需时间2小时,
24.解:(Ⅰ)由已知,根据正弦定理得
即 由余弦定理得
故 ,A=120°
(Ⅱ)由(Ⅰ)得:
故当B=30°时,sinB+sinC取得最大值1。
25.解:设在t时刻台风中心位于点Q,此时|OP|=300,|PQ|=20t,
台风侵袭范围的圆形区域半径为r(t)=10t+60,
由,可知,
cos∠OPQ=cos(θ-45o)= cosθcos45o+ sinθsin45o
=
在 △OPQ中,由余弦定理,得
=
=
若城市O受到台风的侵袭,则有|OQ|≤r(t),即
,
整理,得,解得12≤t≤24,
答:12小时后该城市开始受到台风的侵袭.
