24.1.1圆 课件(共29张PPT)
图片预览





文档简介
(共29张PPT)
24.1.1圆
人教版九年级上册
教学目标
教学目标:1.理解圆的本质属性.
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与
圆有关的概念,并了解它们之间的区别和联系.
3.初步了解点与圆的位置关系.
教学重点:理解圆的本质属性.
教学难点:认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆
有关的概念,并了解它们之间的区别和联系.
新知导入
情境引入
问题: 观察下列图片,找出共同的图形来.
你还能举出生活中的圆的图形吗?
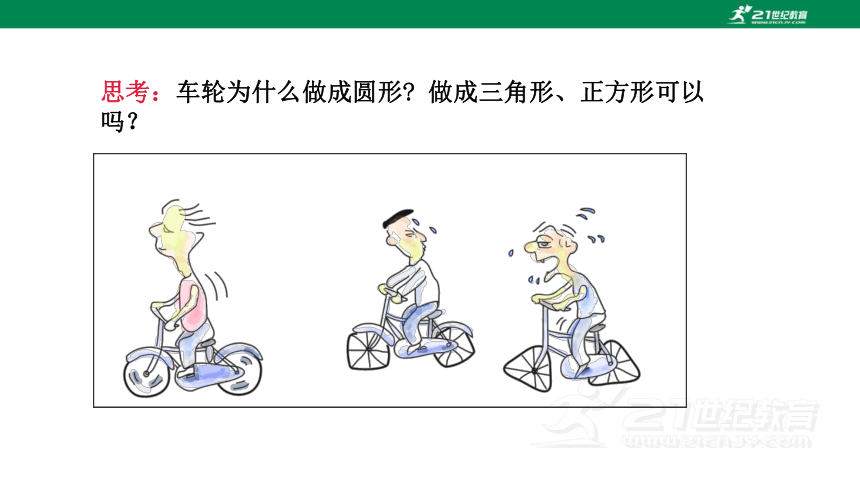
思考:车轮为什么做成圆形 做成三角形、正方形可以吗?
新知讲解
合作学习
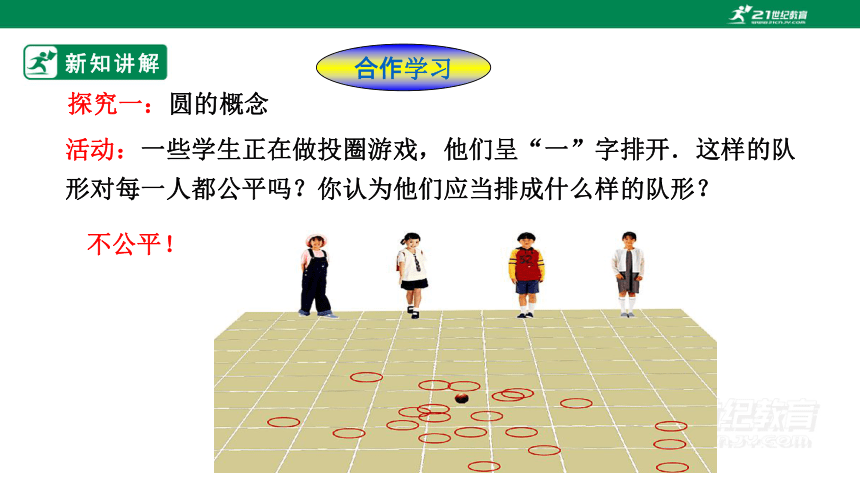
活动:一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
探究一:圆的概念
不公平!
甲
丙
乙
丁
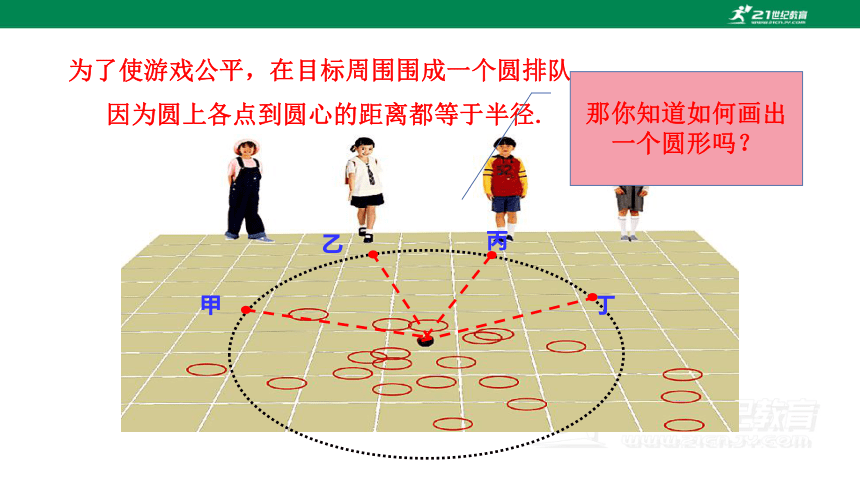
为了使游戏公平,在目标周围围成一个圆排队,
因为圆上各点到圆心的距离都等于半径.
那你知道如何画出一个圆形吗?
思考1:如何在操场上画一个半径是5m的圆?说出你的理由。
·
r
O
A
★圆的旋转定义:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
★相关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
思考2:观察画圆的过程,你能说出圆是如何画出来的吗?
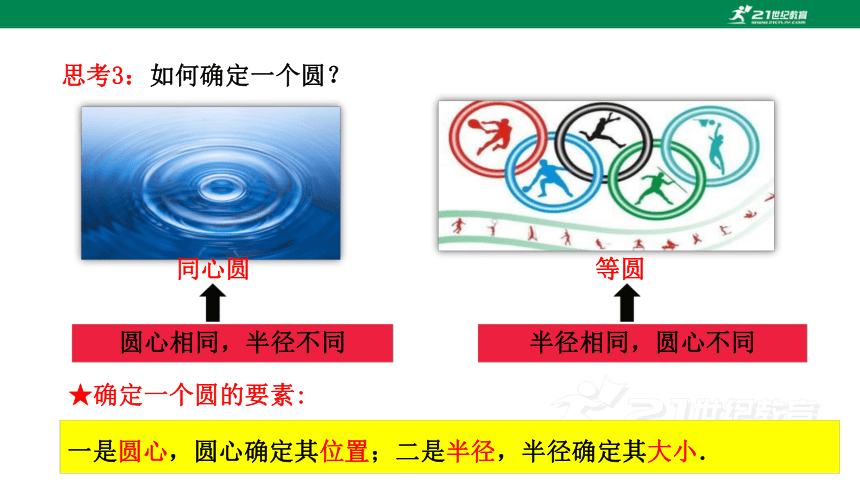
思考3:如何确定一个圆?
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
半径相同,圆心不同
圆心相同,半径不同
★确定一个圆的要素:
同心圆
等圆
合作探究
思考4:从集合角度认识圆,圆是由什么图形构成的?
有间隙吗?
圆也可以看成是由多个点(到定点距离等于定长的)组成的
思考5:反过来,到定点的距离等于定长的点都在同一个圆上吗?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
思考6:从集合的角度看圆,组成圆的图形由什么特点?
提炼概念
★动态:
★静态:
归纳总结:圆的两种定义
在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
圆心为 O,半径为 r 的圆可以看成是所有到定点 O 的距离等于定长 r 的点的集合.
典例精讲
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
又∵AC=BD,
∴OA=OB=OC=OD.
∴AO=OC= AC,OB=OD= BD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
小结 用定义证明几个点在同一个圆上的方法:只要证明这几个点到圆心的距离相等即可 .
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变.因此,当车辆在平坦的路上行驶时,骑车的人会感觉到非常平稳,这就是车轮都做成圆形的数学道理.
趣味生活:自行车的为什么车轮是圆的?
探究二:圆的相关概念
★弦:
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
知识点拨:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,
但弦不一定是直径.
归纳概念
★弧:
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
★劣弧与优弧
★半圆
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
O
A
B
C
O
A
B
★等圆:
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:
等圆是两个半径相等的圆.
★等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
思考7:长度相等的弧是等弧吗?
课堂练习
1.下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm
B.圆心在点O处
C.半径是1 cm,且经过点P
D.圆心在点O处,且直径是2 cm
2.如图,点A,B,C在⊙O上,点O在线段AC上,点D在 线段AB上,下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
3.判断下列说法的正误:
(1)弦是直径;(2)半圆是弧;
(3)过圆心的线段是直径;
(4)半圆是最长的弧;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个半圆是等弧.
×,√,×,×,×,√
4.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
直径
半径
一
二
四
四
5.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
A
B
C
D
O
F
E
6. 如图.
(1)请写出以点B为端点的劣弧及优弧;
(2)请写出以点B为端点的弦及直径;
弦BD, AB, BE.其中弦AB又是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦DF,它所对的弧是 .
A
B
C
E
F
D
O
劣弧:
优弧:
BF,
(
BD,
(
BC,
(
BE.
(
BFE,
(
BFC,
(
BCD,
(
BCF.
(
DF
(
综合演练
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,求∠AOD的度数.
解:∵AD∥OC,
∴∠AOC=∠DAO=70°.
又∵OD=OA,
∴∠ADO=∠DAO=70°.
∴∠AOD=180-70°-70°=40°.
课堂总结
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半 圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.1.1圆
人教版九年级上册
教学目标
教学目标:1.理解圆的本质属性.
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与
圆有关的概念,并了解它们之间的区别和联系.
3.初步了解点与圆的位置关系.
教学重点:理解圆的本质属性.
教学难点:认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆
有关的概念,并了解它们之间的区别和联系.
新知导入
情境引入
问题: 观察下列图片,找出共同的图形来.
你还能举出生活中的圆的图形吗?
思考:车轮为什么做成圆形 做成三角形、正方形可以吗?
新知讲解
合作学习
活动:一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
探究一:圆的概念
不公平!
甲
丙
乙
丁
为了使游戏公平,在目标周围围成一个圆排队,
因为圆上各点到圆心的距离都等于半径.
那你知道如何画出一个圆形吗?
思考1:如何在操场上画一个半径是5m的圆?说出你的理由。
·
r
O
A
★圆的旋转定义:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
★相关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
思考2:观察画圆的过程,你能说出圆是如何画出来的吗?
思考3:如何确定一个圆?
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
半径相同,圆心不同
圆心相同,半径不同
★确定一个圆的要素:
同心圆
等圆
合作探究
思考4:从集合角度认识圆,圆是由什么图形构成的?
有间隙吗?
圆也可以看成是由多个点(到定点距离等于定长的)组成的
思考5:反过来,到定点的距离等于定长的点都在同一个圆上吗?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
思考6:从集合的角度看圆,组成圆的图形由什么特点?
提炼概念
★动态:
★静态:
归纳总结:圆的两种定义
在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
圆心为 O,半径为 r 的圆可以看成是所有到定点 O 的距离等于定长 r 的点的集合.
典例精讲
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
又∵AC=BD,
∴OA=OB=OC=OD.
∴AO=OC= AC,OB=OD= BD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
小结 用定义证明几个点在同一个圆上的方法:只要证明这几个点到圆心的距离相等即可 .
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变.因此,当车辆在平坦的路上行驶时,骑车的人会感觉到非常平稳,这就是车轮都做成圆形的数学道理.
趣味生活:自行车的为什么车轮是圆的?
探究二:圆的相关概念
★弦:
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
知识点拨:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,
但弦不一定是直径.
归纳概念
★弧:
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
★劣弧与优弧
★半圆
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
O
A
B
C
O
A
B
★等圆:
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:
等圆是两个半径相等的圆.
★等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
思考7:长度相等的弧是等弧吗?
课堂练习
1.下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm
B.圆心在点O处
C.半径是1 cm,且经过点P
D.圆心在点O处,且直径是2 cm
2.如图,点A,B,C在⊙O上,点O在线段AC上,点D在 线段AB上,下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
3.判断下列说法的正误:
(1)弦是直径;(2)半圆是弧;
(3)过圆心的线段是直径;
(4)半圆是最长的弧;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个半圆是等弧.
×,√,×,×,×,√
4.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
直径
半径
一
二
四
四
5.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
A
B
C
D
O
F
E
6. 如图.
(1)请写出以点B为端点的劣弧及优弧;
(2)请写出以点B为端点的弦及直径;
弦BD, AB, BE.其中弦AB又是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦DF,它所对的弧是 .
A
B
C
E
F
D
O
劣弧:
优弧:
BF,
(
BD,
(
BC,
(
BE.
(
BFE,
(
BFC,
(
BCD,
(
BCF.
(
DF
(
综合演练
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,求∠AOD的度数.
解:∵AD∥OC,
∴∠AOC=∠DAO=70°.
又∵OD=OA,
∴∠ADO=∠DAO=70°.
∴∠AOD=180-70°-70°=40°.
课堂总结
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半 圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
