6.2.4组合数1 课件(共12张PPT)
文档属性
| 名称 | 6.2.4组合数1 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 356.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 12:00:48 | ||
图片预览





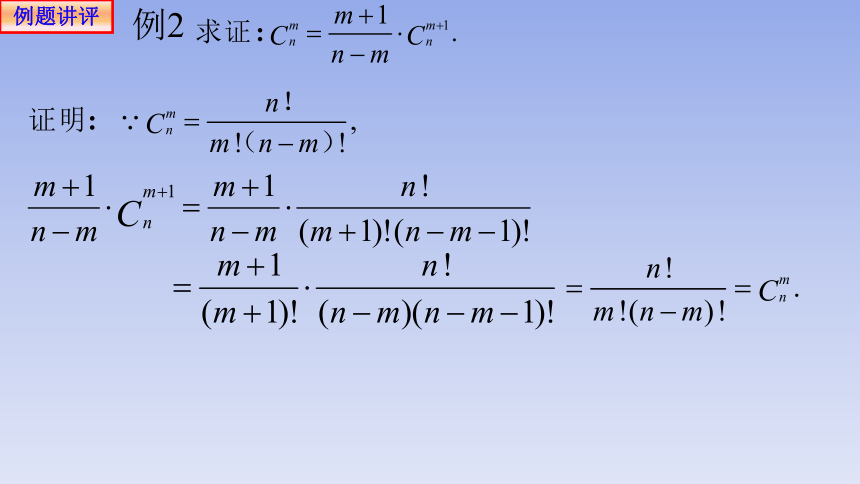
文档简介
(共12张PPT)
6.2.4组合数
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
(1)组合的定义?
复习引入
(2)如何判断一个计数问题是排列问题还是组合问题?
(1)判断是否为组合问题;(2)是否分类或分步;(3)根据组合的相关知识进行求解.
(3).求一个组合问题的所有组合个数的基本方法:
组合数公式:
从 n 个不同元中取出m个元素的排列数
复习引入
组合数公式
1.计算:
复习练习
例1.计算:
解:
例题讲评
例2
例题讲评
巩固练习
1.满足条件>的正整数n的个数是( )
A.10 B.9 C.4 D.3
巩固练习
解:由>得>
所以(n-4)(n-5)<30,所以n -9n-10<0,解得-1由题意,n可取的值是6,7,8,9,共四个,
C
2. + ++···+的值等于( )
A.7351 B.7355 C.7513 D.7315
【解析】原式= + ++···+
= + ++···+= + ++···+=7315,
故选D.
【思路点拨】利用组合数公式和组合数的性质解决.
巩固练习
例3 求证:
例题讲评
练习巩固
例4:在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2)从2件次品中抽出1件的抽法有种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
(3)方法1:从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
方法2:抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
6.2.4组合数
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
(1)组合的定义?
复习引入
(2)如何判断一个计数问题是排列问题还是组合问题?
(1)判断是否为组合问题;(2)是否分类或分步;(3)根据组合的相关知识进行求解.
(3).求一个组合问题的所有组合个数的基本方法:
组合数公式:
从 n 个不同元中取出m个元素的排列数
复习引入
组合数公式
1.计算:
复习练习
例1.计算:
解:
例题讲评
例2
例题讲评
巩固练习
1.满足条件>的正整数n的个数是( )
A.10 B.9 C.4 D.3
巩固练习
解:由>得>
所以(n-4)(n-5)<30,所以n -9n-10<0,解得-1
C
2. + ++···+的值等于( )
A.7351 B.7355 C.7513 D.7315
【解析】原式= + ++···+
= + ++···+= + ++···+=7315,
故选D.
【思路点拨】利用组合数公式和组合数的性质解决.
巩固练习
例3 求证:
例题讲评
练习巩固
例4:在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2)从2件次品中抽出1件的抽法有种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
(3)方法1:从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
方法2:抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
