人教版(2019)高中物理必修一3.5共点力平衡 学案(有解析)
文档属性
| 名称 | 人教版(2019)高中物理必修一3.5共点力平衡 学案(有解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 601.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-02 00:00:00 | ||
图片预览


文档简介
3.5共点力平衡
共点力
作用在物体的同一点,或作用线的延长线交于一点的力。如图所示均是共点力。
甲 乙 丙
共点力合成的方法
(1)作图法:
(2)计算法(三种特殊情况的计算法应用):
类型 作图 合力的计算
互相垂直 F= tan θ=
两力等大, 夹角为θ F=2F1cos F与F1夹角为
两力等大, 夹角为120° 合力与分力等大 F′与F夹角为60°
一、单选题
1.如图,一物块在水平拉力F的作用下沿水平桌面做匀速直线运动.若保持F的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动.物块与桌面间的动摩擦因数为( )
A.2- B. C. D.
【答案】C
【解析】当拉力水平时,物体匀速运动,则拉力等于摩擦力,即:,当拉力倾斜时,物体受力分析如图
由平衡条件得:,,又,得摩擦力为:,联立解得:,故选C.
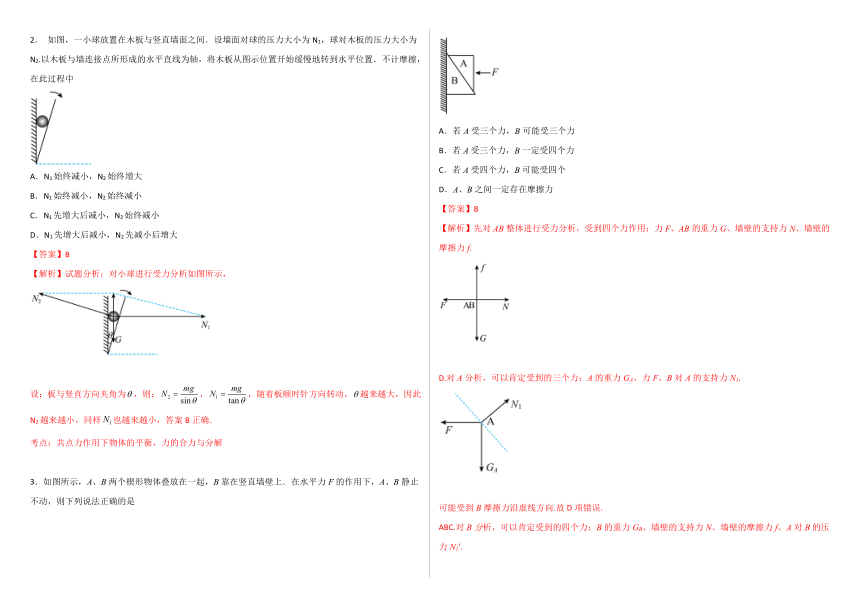
2. 如图,一小球放置在木板与竖直墙面之间.设墙面对球的压力大小为N1,球对木板的压力大小为N2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中
A.N1始终减小,N2始终增大
B.N1始终减小,N2始终减小
C.N1先增大后减小,N2始终减小
D.N1先增大后减小,N2先减小后增大
【答案】B
【解析】试题分析:对小球进行受力分析如图所示,
设:板与竖直方向夹角为,则:,,随着板顺时针方向转动,越来越大,因此N2越来越小,同样也越来越小,答案B正确.
考点:共点力作用下物体的平衡,力的合力与分解
3.如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上.在水平力F的作用下,A、B静止不动,则下列说法正确的是
A.若A受三个力,B可能受三个力
B.若A受三个力,B一定受四个力
C.若A受四个力,B可能受四个
D.A、B之间一定存在摩擦力
【答案】B
【解析】先对AB整体进行受力分析,受到四个力作用:力F、AB的重力G、墙壁的支持力N、墙壁的摩擦力f.
D.对A分析,可以肯定受到的三个力:A的重力GA、力F、B对A的支持力N1.
可能受到B摩擦力沿虚线方向.故D项错误.
ABC.对B分析,可以肯定受到的四个力:B的重力GB、墙壁的支持力N、墙壁的摩擦力f、A对B的压力N1'.
可能受到A摩擦力沿虚线方向.故A项错误,C项错误,B项正确.
4.如图,滑块A置于水平地面上,滑块B在一水平力作用下紧靠滑块(A、B接触面竖直,此时A恰好不滑动,B刚好不下滑,已知A与B间的动摩擦因数为,A与地面间的动摩擦因数为,最大静摩擦力等于滑动摩擦力,与B的质量之比为
A. B. C. D.
【答案】B
【解析】试题分析:对A、B整体分析,受重力、支持力、推力和最大静摩擦力,根据平衡条件,有:
F=μ2(m1+m2)g ①
再对物体B分析,受推力、重力、向左的支持力和向上的最大静摩擦力,根据平衡条件,有:
水平方向:F=N
竖直方向:m2g=f
其中:f=μ1N
联立有:m2g=μ1F ②
联立①②解得:
故选B。
5.在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3.若F缓慢增大而整个装置仍保持静止,截面如图所示,在此过程中( )
A.F1保持不变,F3缓慢增大
B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大
D.F2缓慢增大,F3保持不变
【答案】C
【解析】对B分析,可知墙对B的作用力及A对球的作用力的合力与F及重力的合力大小相等,方向相反,故当F增大时,B对A的压力增大;即F2增大;同理可知,墙对B的作用力F1增大;
对整体分析,整体受重力、支持力、摩擦力及压力F而处于平衡,故当F增大时,地面对A的支持力增大;故F3增大;但水平方向力不变;故选C.
6.如图所示,小球用细绳系住,绳的另一端固定于O点,现用水平F缓慢推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力FN,以及绳对小球的拉力FT的变化情况是( )
A.FN保持不变,FT不断增大 B.FN不断增大,FT不断减小
C.FN保持不变,FT先增大后减小 D.FN不断增大,FT先减小后增大
【答案】D
【解析】对小球进行受力分析,重力、支持力FN、拉力FT组成一个闭合的矢量三角形,由于重力不变、支持力FN方向不变,斜面向左移动的过程中,拉力FT与水平方向的夹角β减小,当β=θ时,FT⊥FN,细绳的拉力FT最小,由图可知,随β的减小,斜面的支持力FN不断增大,FT先减小后增大.故D正确,ABC错误.
7.如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等。系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=70°,则β等于( )
A.45° B.55° C.60° D.70°
【答案】B
【解析】甲物体是拴牢在O点,且甲、乙两物体的质量相等,则甲、乙绳的拉力大小相等,O点处于平衡状态,则左侧绳子拉力的方向在甲、乙绳子的角平分线上,如图所示
根据几何关系有
解得。
故选B。
8.质量为的凹槽静止在水平地面上,内壁为半圆柱面,截面如图所示,为半圆的最低点,为半圆水平直径的端点。凹槽恰好与竖直墙面接触,内有一质量为的小滑块。用推力推动小滑块由A点向点缓慢移动,力的方向始终沿圆弧的切线方向,在此过程中所有摩擦均可忽略,下列说法正确的是( )
A.推力先增大后减小
B.凹槽对滑块的支持力先减小后增大
C.墙面对凹槽的压力先增大后减小
D.水平地面对凹槽的支持力先减小后增大
【答案】C
【解析】AB .对滑块受力分析,由平衡条件有
滑块从A缓慢移动B点时,越来越大,则推力F越来越大,支持力N越来越小,所以AB错误;
C.对凹槽与滑块整体分析,有墙面对凹槽的压力为
则越来越大时,墙面对凹槽的压力先增大后减小,所以C正确;
D.水平地面对凹槽的支持力为
则越来越大时,水平地面对凹槽的支持力越来越小,所以D错误;
故选C。
二、解答题
9.如图甲所示,轻杆OB可绕B点自由转动,另一端O点用细绳拉住,固定在左侧墙壁上,质量为m的重物用细绳OC悬挂在轻杆的O点,OA与轻杆的夹角∠BOA=30°。乙图中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根绳跨过滑轮后悬挂一质量为m的重物,图中∠BOA=30°,求:
(1)甲、乙两图中细绳OA的拉力各是多大?
(2)甲图中轻杆受到的弹力是多大?
(3)乙图中轻杆对滑轮的作用力是多大?
【答案】(1)2mg,mg;(2);(3)mg
【解析】 (1)图甲中,以O点为研究对象,受力分析得
根据平衡条件得
,
图乙中,对绳子上的O点分析
受力平衡,有
(2)由牛顿第三定律:图甲中OB杆受到的弹力
(3)乙图中,根据题意可得,对O点受力分析
滑轮受到绳子的作用力应为图中两段绳中拉力F1和F2的合力F,因同一根绳张力处处相等,都等于物体的重量,即
用平行四边形定则作图,因为拉力F1和F2的夹角为120°,则由几何知识得
乙图中,由于平衡,则 轻杆对滑轮的作用力和轻绳对滑轮的作用力大小相等,方向相反,即
10.如图所示,质量为的木板B放在水平地面上,质量为的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面绳绷紧时与水平面的夹角为.已知货箱A与木板B之间的动摩擦因数,木板B与地面之间的动摩擦因数.重力加速度g取.现用水平力F将木板B从货箱A下面匀速抽出,试求:(,)
(1)绳上张力T的大小;
(2)拉力F的大小.
【答案】(1)100N (2)200N
【解析】 (1)对物体A受力分析如图所示:
A静止,受力平衡,则在x轴上:Tcosθ=f1
在y轴上:N1=Tsinθ+mAg
又f1=μ1 N1
联立解得:
T=100 N
f=80N
即绳上张力T的大小为100N.
(2)对物体B受力分析如图所示:
B处于静止,根据平衡条件可得:
在x轴上:F=f1+f2
在y轴上:N2=N1+mBg
又有:f2=μ2N2
联立解得:
F=200 N
即拉力F的大小为200N.
11.如图所示,质量M=5.5kg的木块套在水平固定杆上,并用轻绳与质量m=1kg的小球相连。今用跟水平方向成60°角的力F=10N拉着球并带动木块一起向右匀速运动,运动中M、m相对位置保持不变,g取10m/s2。求:
(1)轻绳与水平方向夹角θ;
(2)木块M与水平杆间的动摩擦因数μ。
【答案】(1)30°;(2)
【解析】 (1)m处于平衡状态,受到重力、拉力F和轻绳拉力FT,如图所示
以m为研究对象,由平衡条件得
水平方向
Fcos60°-FTcosθ=0①
竖直方向
Fsin60°-FTsinθ-mg=0②
①②联立解得
θ=30°
(2)以M、m整体为研究对象,设杆对M的支持力为FN,由平衡条件得
水平方向
Fcos60°-μFN=0③
竖直方向
FN+Fsin60°-Mg-mg=0④
由③④解得
12.如图所示,质量为m的物体放在一固定斜面上,当斜面倾角为30°时恰能沿斜面匀速下滑.对物体施加一大小为F、方向水平向右的恒力,物体可沿斜面匀速向上滑行.设最大静摩擦力等于滑动摩擦力,当斜面倾角增大并超过某一临界角θ0时,不论水平恒力F多大,都不能使物体沿斜面向上滑行,试求:
(1)物体与斜面间的动摩擦因数;
(2)这一临界角θ0的大小.
【答案】(1)(2)60°
【解析】试题分析:(1)斜面倾角为30°时,物体恰能匀速下滑,满足
解得
(2)设斜面倾角为α,由匀速直线运动的条件:
,
解得:
当,即时,F→∞,
即“不论水平恒力F多大”,都不能使物体沿斜面向上滑行此时,临界角
考点:考查了共点力平衡条件的应用
共点力
作用在物体的同一点,或作用线的延长线交于一点的力。如图所示均是共点力。
甲 乙 丙
共点力合成的方法
(1)作图法:
(2)计算法(三种特殊情况的计算法应用):
类型 作图 合力的计算
互相垂直 F= tan θ=
两力等大, 夹角为θ F=2F1cos F与F1夹角为
两力等大, 夹角为120° 合力与分力等大 F′与F夹角为60°
一、单选题
1.如图,一物块在水平拉力F的作用下沿水平桌面做匀速直线运动.若保持F的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动.物块与桌面间的动摩擦因数为( )
A.2- B. C. D.
【答案】C
【解析】当拉力水平时,物体匀速运动,则拉力等于摩擦力,即:,当拉力倾斜时,物体受力分析如图
由平衡条件得:,,又,得摩擦力为:,联立解得:,故选C.
2. 如图,一小球放置在木板与竖直墙面之间.设墙面对球的压力大小为N1,球对木板的压力大小为N2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中
A.N1始终减小,N2始终增大
B.N1始终减小,N2始终减小
C.N1先增大后减小,N2始终减小
D.N1先增大后减小,N2先减小后增大
【答案】B
【解析】试题分析:对小球进行受力分析如图所示,
设:板与竖直方向夹角为,则:,,随着板顺时针方向转动,越来越大,因此N2越来越小,同样也越来越小,答案B正确.
考点:共点力作用下物体的平衡,力的合力与分解
3.如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上.在水平力F的作用下,A、B静止不动,则下列说法正确的是
A.若A受三个力,B可能受三个力
B.若A受三个力,B一定受四个力
C.若A受四个力,B可能受四个
D.A、B之间一定存在摩擦力
【答案】B
【解析】先对AB整体进行受力分析,受到四个力作用:力F、AB的重力G、墙壁的支持力N、墙壁的摩擦力f.
D.对A分析,可以肯定受到的三个力:A的重力GA、力F、B对A的支持力N1.
可能受到B摩擦力沿虚线方向.故D项错误.
ABC.对B分析,可以肯定受到的四个力:B的重力GB、墙壁的支持力N、墙壁的摩擦力f、A对B的压力N1'.
可能受到A摩擦力沿虚线方向.故A项错误,C项错误,B项正确.
4.如图,滑块A置于水平地面上,滑块B在一水平力作用下紧靠滑块(A、B接触面竖直,此时A恰好不滑动,B刚好不下滑,已知A与B间的动摩擦因数为,A与地面间的动摩擦因数为,最大静摩擦力等于滑动摩擦力,与B的质量之比为
A. B. C. D.
【答案】B
【解析】试题分析:对A、B整体分析,受重力、支持力、推力和最大静摩擦力,根据平衡条件,有:
F=μ2(m1+m2)g ①
再对物体B分析,受推力、重力、向左的支持力和向上的最大静摩擦力,根据平衡条件,有:
水平方向:F=N
竖直方向:m2g=f
其中:f=μ1N
联立有:m2g=μ1F ②
联立①②解得:
故选B。
5.在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3.若F缓慢增大而整个装置仍保持静止,截面如图所示,在此过程中( )
A.F1保持不变,F3缓慢增大
B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大
D.F2缓慢增大,F3保持不变
【答案】C
【解析】对B分析,可知墙对B的作用力及A对球的作用力的合力与F及重力的合力大小相等,方向相反,故当F增大时,B对A的压力增大;即F2增大;同理可知,墙对B的作用力F1增大;
对整体分析,整体受重力、支持力、摩擦力及压力F而处于平衡,故当F增大时,地面对A的支持力增大;故F3增大;但水平方向力不变;故选C.
6.如图所示,小球用细绳系住,绳的另一端固定于O点,现用水平F缓慢推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力FN,以及绳对小球的拉力FT的变化情况是( )
A.FN保持不变,FT不断增大 B.FN不断增大,FT不断减小
C.FN保持不变,FT先增大后减小 D.FN不断增大,FT先减小后增大
【答案】D
【解析】对小球进行受力分析,重力、支持力FN、拉力FT组成一个闭合的矢量三角形,由于重力不变、支持力FN方向不变,斜面向左移动的过程中,拉力FT与水平方向的夹角β减小,当β=θ时,FT⊥FN,细绳的拉力FT最小,由图可知,随β的减小,斜面的支持力FN不断增大,FT先减小后增大.故D正确,ABC错误.
7.如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等。系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=70°,则β等于( )
A.45° B.55° C.60° D.70°
【答案】B
【解析】甲物体是拴牢在O点,且甲、乙两物体的质量相等,则甲、乙绳的拉力大小相等,O点处于平衡状态,则左侧绳子拉力的方向在甲、乙绳子的角平分线上,如图所示
根据几何关系有
解得。
故选B。
8.质量为的凹槽静止在水平地面上,内壁为半圆柱面,截面如图所示,为半圆的最低点,为半圆水平直径的端点。凹槽恰好与竖直墙面接触,内有一质量为的小滑块。用推力推动小滑块由A点向点缓慢移动,力的方向始终沿圆弧的切线方向,在此过程中所有摩擦均可忽略,下列说法正确的是( )
A.推力先增大后减小
B.凹槽对滑块的支持力先减小后增大
C.墙面对凹槽的压力先增大后减小
D.水平地面对凹槽的支持力先减小后增大
【答案】C
【解析】AB .对滑块受力分析,由平衡条件有
滑块从A缓慢移动B点时,越来越大,则推力F越来越大,支持力N越来越小,所以AB错误;
C.对凹槽与滑块整体分析,有墙面对凹槽的压力为
则越来越大时,墙面对凹槽的压力先增大后减小,所以C正确;
D.水平地面对凹槽的支持力为
则越来越大时,水平地面对凹槽的支持力越来越小,所以D错误;
故选C。
二、解答题
9.如图甲所示,轻杆OB可绕B点自由转动,另一端O点用细绳拉住,固定在左侧墙壁上,质量为m的重物用细绳OC悬挂在轻杆的O点,OA与轻杆的夹角∠BOA=30°。乙图中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根绳跨过滑轮后悬挂一质量为m的重物,图中∠BOA=30°,求:
(1)甲、乙两图中细绳OA的拉力各是多大?
(2)甲图中轻杆受到的弹力是多大?
(3)乙图中轻杆对滑轮的作用力是多大?
【答案】(1)2mg,mg;(2);(3)mg
【解析】 (1)图甲中,以O点为研究对象,受力分析得
根据平衡条件得
,
图乙中,对绳子上的O点分析
受力平衡,有
(2)由牛顿第三定律:图甲中OB杆受到的弹力
(3)乙图中,根据题意可得,对O点受力分析
滑轮受到绳子的作用力应为图中两段绳中拉力F1和F2的合力F,因同一根绳张力处处相等,都等于物体的重量,即
用平行四边形定则作图,因为拉力F1和F2的夹角为120°,则由几何知识得
乙图中,由于平衡,则 轻杆对滑轮的作用力和轻绳对滑轮的作用力大小相等,方向相反,即
10.如图所示,质量为的木板B放在水平地面上,质量为的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面绳绷紧时与水平面的夹角为.已知货箱A与木板B之间的动摩擦因数,木板B与地面之间的动摩擦因数.重力加速度g取.现用水平力F将木板B从货箱A下面匀速抽出,试求:(,)
(1)绳上张力T的大小;
(2)拉力F的大小.
【答案】(1)100N (2)200N
【解析】 (1)对物体A受力分析如图所示:
A静止,受力平衡,则在x轴上:Tcosθ=f1
在y轴上:N1=Tsinθ+mAg
又f1=μ1 N1
联立解得:
T=100 N
f=80N
即绳上张力T的大小为100N.
(2)对物体B受力分析如图所示:
B处于静止,根据平衡条件可得:
在x轴上:F=f1+f2
在y轴上:N2=N1+mBg
又有:f2=μ2N2
联立解得:
F=200 N
即拉力F的大小为200N.
11.如图所示,质量M=5.5kg的木块套在水平固定杆上,并用轻绳与质量m=1kg的小球相连。今用跟水平方向成60°角的力F=10N拉着球并带动木块一起向右匀速运动,运动中M、m相对位置保持不变,g取10m/s2。求:
(1)轻绳与水平方向夹角θ;
(2)木块M与水平杆间的动摩擦因数μ。
【答案】(1)30°;(2)
【解析】 (1)m处于平衡状态,受到重力、拉力F和轻绳拉力FT,如图所示
以m为研究对象,由平衡条件得
水平方向
Fcos60°-FTcosθ=0①
竖直方向
Fsin60°-FTsinθ-mg=0②
①②联立解得
θ=30°
(2)以M、m整体为研究对象,设杆对M的支持力为FN,由平衡条件得
水平方向
Fcos60°-μFN=0③
竖直方向
FN+Fsin60°-Mg-mg=0④
由③④解得
12.如图所示,质量为m的物体放在一固定斜面上,当斜面倾角为30°时恰能沿斜面匀速下滑.对物体施加一大小为F、方向水平向右的恒力,物体可沿斜面匀速向上滑行.设最大静摩擦力等于滑动摩擦力,当斜面倾角增大并超过某一临界角θ0时,不论水平恒力F多大,都不能使物体沿斜面向上滑行,试求:
(1)物体与斜面间的动摩擦因数;
(2)这一临界角θ0的大小.
【答案】(1)(2)60°
【解析】试题分析:(1)斜面倾角为30°时,物体恰能匀速下滑,满足
解得
(2)设斜面倾角为α,由匀速直线运动的条件:
,
解得:
当,即时,F→∞,
即“不论水平恒力F多大”,都不能使物体沿斜面向上滑行此时,临界角
考点:考查了共点力平衡条件的应用
