人教版(2019)高中物理必修一4.5牛顿运动定律的应用 学案(有解析)
文档属性
| 名称 | 人教版(2019)高中物理必修一4.5牛顿运动定律的应用 学案(有解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-02 18:06:36 | ||
图片预览



文档简介
4.5牛顿运动定律的应用
一、动力学两类基本问题
1.动力学的两类基本问题
第一类:已知物体的受力情况求运动情况;
第二类:已知物体的运动情况求受力情况。
2.解决两类基本问题的方法
以加速度为“桥梁”,由运动学公式和牛顿运动定律列方程求解,具体逻辑关系如图:
1.问题类型
2.解决动力学两类问题的两个关键点
3.动力学基本问题中力的处理方法
(1)合成法:在物体受力个数较少(2个或3个)时一般采用“合成法”。
(2)正交分解法:若物体的受力个数较多(3个或3个以上),则采用“正交分解法”。
一、单选题
1.如图所示,2022北京冬奥会冰壶比赛时某运动员将冰壶(可视为质点)以速度从栏线P沿虚线推出,假设冰壶沿虚线做匀减速直线运动,栏线P到营垒圆心O的距离是,营垒是由4个直径分别为和的同心圆组成。冰壶与冰面的动摩擦因数,运动员把冰壶推进直径是的圆内,重力加速度g取,则可能是( )
A. B.
C. D.
【答案】C
【解析】冰壶在冰面上沿虚线做减速直线运动,把冰壶推进直径是的圆内,冰壶匀减速运动到0的位移
也就是位移满足
加速度大小
根据运动学公式
代入数据得
故选C。
2.中欧班列在欧亚大陆开辟了“生命之路”,为国际抗疫贡献了中国力量。某运送防疫物资的班列由40节质量相等的车厢组成,在车头牵引下,列车沿平直轨道匀加速行驶时,第2节对第3节车厢的牵引力为F。若每节车厢所受摩擦力、空气阻力均相等,则倒数第3节对倒数第2节车厢的牵引力为( )
A.F B. C. D.
【答案】C
【解析】根据题意可知第2节车厢对第3节车厢的牵引力为F,因为每节车厢质量相等,阻力相同,故第2节对第3节车厢根据牛顿第二定律有
设倒数第3节车厢对倒数第2节车厢的牵引力为F1,则根据牛顿第二定律有
联立解得。
故选C。
3.一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图像如图所示。乘客所受支持力的大小用FN表示,速度大小用v表示。重力加速度大小为g。以下判断正确的是( )
A.0~t1时间内,v增大,FN>mg B.t1~t2时间内,v减小,FNC.t2~t3时间内,v增大,FN mg
【答案】D
【解析】A.由于s-t图像的斜率表示速度,可知在0~t1时间内速度增加,即乘客的加速度向下,处于失重状态,则FNB.在t1~t2时间内速度不变,即乘客的匀速下降,则FN=mg,选项B错误;
CD.在t2~t3时间内速度减小,即乘客的减速下降,超重,则FN>mg,选项C错误,D正确;
故选D。
4.如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是
A.小车静止时,,方向沿杆向上
B.小车静止时,,方向垂直杆向上
C.小车向右以加速度a运动时,一定有
D.小车向左以加速度a运动时,
【答案】D
【解析】当小车静止时,球处于平衡状态,则杆对小球的作用力F=mg,方向竖直向上.故AB错误.当小车向右以加速度a运动时,则球的合力为F合=ma,根据平行四边形定则知,杆对球的作用力F=,因为杆对球的作用力方向不一定沿杆,则作用力不一定等于.故C错误,D正确.故选D.
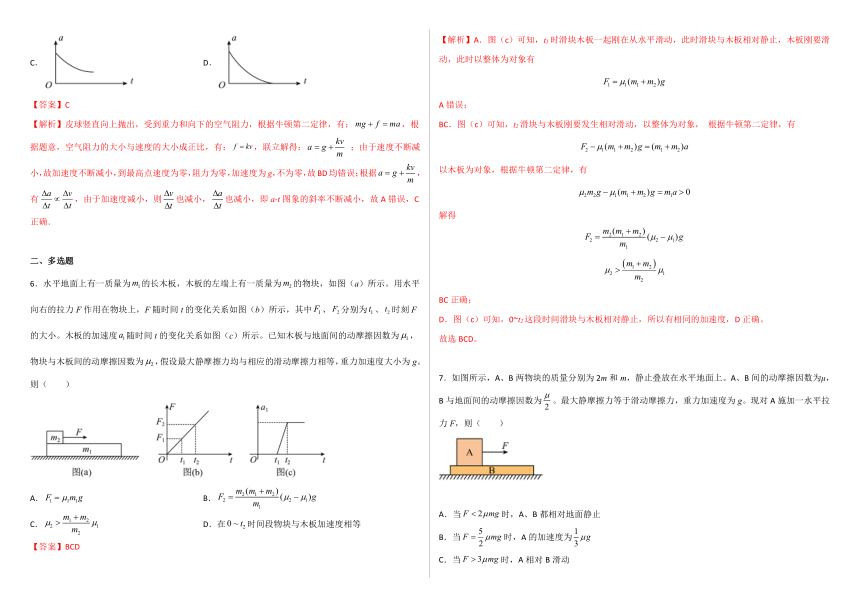
5.将一只皮球竖直向上抛出,皮球运动时受到空气阻力的大小与速度的大小成正比.下列描绘皮球在上升过程中加速度大小a与时间t关系的图象,可能正确的是
A. B.
C. D.
【答案】C
【解析】皮球竖直向上抛出,受到重力和向下的空气阻力,根据牛顿第二定律,有:,根据题意,空气阻力的大小与速度的大小成正比,有:,联立解得: ;由于速度不断减小,故加速度不断减小,到最高点速度为零,阻力为零,加速度为g,不为零,故BD均错误;根据,有,由于加速度减小,则也减小,也减小,即a-t图象的斜率不断减小,故A错误,C正确.
二、多选题
6.水平地面上有一质量为的长木板,木板的左端上有一质量为的物块,如图(a)所示。用水平向右的拉力F作用在物块上,F随时间t的变化关系如图(b)所示,其中、分别为、时刻F的大小。木板的加速度随时间t的变化关系如图(c)所示。已知木板与地面间的动摩擦因数为,物块与木板间的动摩擦因数为,假设最大静摩擦力均与相应的滑动摩擦力相等,重力加速度大小为g。则( )
A. B.
C. D.在时间段物块与木板加速度相等
【答案】BCD
【解析】A.图(c)可知,t1时滑块木板一起刚在从水平滑动,此时滑块与木板相对静止,木板刚要滑动,此时以整体为对象有
A错误;
BC.图(c)可知,t2滑块与木板刚要发生相对滑动,以整体为对象, 根据牛顿第二定律,有
以木板为对象,根据牛顿第二定律,有
解得
BC正确;
D.图(c)可知,0~t2这段时间滑块与木板相对静止,所以有相同的加速度,D正确。
故选BCD。
7.如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上。A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为。最大静摩擦力等于滑动摩擦力,重力加速度为g。现对A施加一水平拉力F,则( )
A.当时,A、B都相对地面静止
B.当时,A的加速度为
C.当时,A相对B滑动
D.无论F为何值,B的加速度不会超过
【答案】BCD
【解析】A.根据题意可知,B与地面间的最大静摩擦力为
因此要使B能够相对地面滑动,A对B所施加的摩擦力至少为
A、B间的最大静摩擦力为
故时,A、B都相对地面静止,A错误;
B.A、B恰好不相对滑动时,根据牛顿第二定律可知应当满足
且
即
则当≤F<3μmg,A、B将一起向右加速滑动。当时,对A和B整体受力分析有
解得
故B正确。
CD.当F≥3μmg时,A、B将以不同的加速度向右滑动,根据牛顿第二定律有
F-2μmg=2maA,
解得
,
故CD正确。
故选BCD。
8.如图所示,将两相同的木块a、b至于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁,开始时a、b均静止。弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力,b所受摩擦力,现将右侧细绳剪断,则剪断瞬间 ( )
A.大小不变 B.方向改变
C.仍然为零 D.方向向右
【答案】AD
【解析】初始状态,a在水平方向上受绳子拉力、弹簧的弹力还有摩擦力处于平衡,b受弹簧的弹力和绳子的拉力处于平衡,右侧细绳剪断的瞬间,弹簧的弹力不变,a仍然受三个力作用,摩擦力的大小和方向不变,而b受到向左的弹力,将受到向右的摩擦力,故选AD。
三、解答题
9.如图所示,一倾斜固定的传送带与水平面间夹角θ=37°,上下两端间距L=2.0m,传送带以v=1.0m/s的速率沿顺时针方向匀速运行。从距离传送带底端x0=1.0m的O点由静止释放一质量m=1.0kg的小滑块,滑块运动到传送带底端时与固定挡板P碰撞,碰撞时间极短且碰撞前后速率相等。滑块与传送带间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,取g=10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求:
(1)滑块与挡板P第一次碰撞时的速度大小v1;
(2)滑块与挡板P碰撞后离开挡板的最大距离xm;
(3)若滑块与挡板P第一次碰撞后立即在滑块上加一方向沿传送带斜向上、大小F=4.0N的恒力,一段时间后撤去。要使滑块能滑至传送带最上端,恒力持续作用的最短时间t。
【答案】(1)2m/s;(2)0.4m;(3)
【解析】(1)设滑块向下运动的加速度为a1,根据牛顿第二定律可得
由匀变速运动规律有
联立解得
v1=2m/s
(2)滑块第一次与挡板碰撞后速度大于传送带速度,滑块减速上滑,设碰后运动的加速度大小为a2,则
减速至与皮带速度相等时运动的距离为x1,则
之后滑块继续减速上滑至速度为零,加速度大小为a1,则
离开挡板的最大距离为
xm=x1+x2
联立解得
xm=0.4m
(3)滑块与挡板碰撞后,在恒力作用下的加速度大小设为a3,根据牛顿第二定律有
设该过程向上运动的距离为x3,运动时间为t1,则
解得
,
接着滑块向上匀速运动,最后撤去拉力再以a1向上减速,减速的距离应为x2,设匀
速运动的时间为t2,则
恒力持续作用的最短时间为
联立解得
10.如图,两个滑块A和B的质量分别为mA=1 kg和mB=5 kg,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4 kg,与地面间的动摩擦因数为μ2=0.1。某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3 m/s,A、B相遇时,A与木板恰好相对静止。设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10 m/s2,求:
(1)B与木板相对静止时,木板的速度;
(2)A、B开始运动时,两者之间的距离。
【答案】(1)1m/s;(2)1.9m。
【解析】(1)滑块A和B在木板上滑动时,木板也在地面上滑动,设A、B和木板所受的摩擦力大小分别为f1、f2和f3,A和B相对于地面的加速度大小分别是aA和aB,木板相对于地面的加速度大小为a1,在物块B与木板达到共同速度前有
①
②
③
由牛顿第二定律得
④
⑤
⑥
设在t1时刻,B与木板达到共同速度,设大小为v1。由运动学公式有
⑦
⑧
联立①②③④⑤⑥⑦⑧式,代入已知数据,可得B与木板相对静止时,木板的速度
⑨
(2)在t1时间间隔内,B相对于地面移动的距离为
⑩
设在B与木板达到共同速度v1后,木板的加速度大小为a2,对于B与木板组成的体系,由牛顿第二定律有
由①②④⑤式知,aA=aB;再由⑦⑧可知,B与木板达到共同速度时,A的速度大小也为v1,但运动方向与木板相反;由题意知,A和B相遇时,A与木板的速度相同,设其大小为v2,设A的速度大小从v1变到v2所用时间为t2,则由运动学公式,对木板有
对A有
在t2时间间隔内,B(以及木板)相对地面移动的距离为
在(t1+t2)时间间隔内,A相对地面移动的距离为
A和B相遇时,A与木板的速度也恰好相同,因此A和B开始运动时,两者之间的距离为
联立以上各式,代入数据,A、B开始运动时,两者之间的距离
答:(1)B与木板相对静止时,木板的速度为1m/s;(2)A、B开始运动时,两者之间的距离为1.9m。
11.一长木板置于粗糙水平地面上,木板左端放置一小物块,在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示.时刻开始,小物块与木板一起以共同速度向右运动,直至时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的图线如图(b)所示.木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求
(1)木板与地面间的动摩擦因数及小物块与木板间的动摩擦因数;
(2)木板的最小长度;
(3)木板右端离墙壁的最终距离.
【答案】(1),;(2);(3)
【解析】(1)根据图像可以判定碰撞前木块与木板共同速度为
碰撞后木板速度水平向左,大小也是
木块受到滑动摩擦力而向右做匀减速,根据牛顿第二定律有
解得
木板与墙壁碰撞前,匀减速运动时间,位移,末速度
其逆运动则为匀加速直线运动可得
带入可得
木块和木板整体受力分析,滑动摩擦力提供合外力,即
可得
(2)碰撞后,木板向左匀减速,依据牛顿第二定律有
可得
对滑块,则有加速度
滑块速度先减小到0,此时碰后时间为
此时,木板向左的位移为末速度
滑块向右位移
此后,木块开始向左加速,加速度仍为
木块继续减速,加速度仍为
假设又经历二者速度相等,则有
解得
此过程,木板位移末速度
滑块位移
此后木块和木板一起匀减速.
二者的相对位移最大为
滑块始终没有离开木板,所以木板最小的长度为
(3)最后阶段滑块和木板一起匀减速直到停止,整体加速度
位移
所以木板右端离墙壁最远的距离为
12.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为m的小物块a相连,如图所示。质量为的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0,从t=0时开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。求:
(1)弹簧的劲度系数;
(2)物块b加速度的大小;
(3)在物块a、b分离前,外力大小随时间变化的关系式。
【答案】(1) (2) (3)
【解析】 (1)对整体分析,根据平衡条件可知,沿斜面方向上重力的分力与弹簧弹力平衡,则有:
kx0=(m+ m)gsinθ
解得
k=
(2)由题意可知,b经两段相等的时间位移为x0;
由匀变速直线运动相邻相等时间内位移关系的规律可知
说明当形变量为时二者分离;
对m分析,因分离时ab间没有弹力,则根据牛顿第二定律可知
kx1-mgsinθ=ma
联立解得
a=
(3)设时间为t,则经时间t时,ab前进的位移
x=at2=
则形变量变为
△x=x0-x
对整体分析可知,由牛顿第二定律有
F+k△x-(m+m)gsinθ=(m+m)a
解得
F= mgsinθ+t2
因分离时位移x=由
x==at2
解得
故应保证0≤t<,F表达式才能成立。
13.如图甲所示,质量为2kg的木板B静止在水平面上.某时刻物块A(可视为质点)从木板的左侧沿木板上表面滑上木板,初速度v0=4m/s.此后A和B运动的v-t图象如图乙所示,取重力加速度g=10m/s2,求:
(1)A与B上表面之间的动摩擦因数μ1;
(2)B与水平面间的动摩擦因数μ2;
(3)A的质量.
【答案】(1)0.2 (2)0.1 (3)6kg
【解析】A滑上B做匀减速直线运动,根据速度时间图线得出匀减速运动的加速度大小,根据牛顿第二定律求出A与B之间的动摩擦因数;A、B速度相同后,一起做匀减速运动,根据速度时间图线求出匀减速运动的加速度大小,结合牛顿第二定律求出与水平面间的动摩擦因数;隔离对M分析,根据速度时间图线得出B的加速度,根据牛顿第二定律求出A的质量.
(1)由图象可知,A在0~1 s内的加速度
对A由牛顿第二定律得,-μ1mg=ma1
解得:μ1=0.2
(2)由图象知,A、B在1~3 s内的加速度
对A、B整体由牛顿第二定律得:-(M+m)gμ2=(M+m)a3
解得:μ2=0.1
(3)由图象可知B在0~1 s内的加速度
对B由牛顿第二定律得,μ1mg-μ2(M+m)g=Ma2
代入数据解得:m=6 kg
14.如图所示,一沿水平方向做匀加速直线运动的车厢中,悬挂小球的悬线偏离竖直方向的夹角,小球和车厢相对静止,小球的质量为,取,,,求:
(1)车厢运动的加速度;
(2)悬线对小球的拉力大小.
【答案】(1),方向水平向右(2)12.5N
【解析】解法一 矢量合成法
(1)选小球为研究对象,对其进行受力分析如图所示,有
又由牛顿第二定律得
则小球的加速度大小为
小球和车厢相对静止,故车厢的加速度大小也为,方向水平向右.
(2)悬线对小球的拉力大小为
.
解法二 正交分解法
建立直角坐标系,并将悬线对小球的拉力正交分解,因小球和车厢相对静止,则沿水平方向有
(为车厢的加速度)
沿竖直方向有
联立以上两式得, ,的方向水平向右.
车厢的加速度大小也为,方向水平向右.
一、动力学两类基本问题
1.动力学的两类基本问题
第一类:已知物体的受力情况求运动情况;
第二类:已知物体的运动情况求受力情况。
2.解决两类基本问题的方法
以加速度为“桥梁”,由运动学公式和牛顿运动定律列方程求解,具体逻辑关系如图:
1.问题类型
2.解决动力学两类问题的两个关键点
3.动力学基本问题中力的处理方法
(1)合成法:在物体受力个数较少(2个或3个)时一般采用“合成法”。
(2)正交分解法:若物体的受力个数较多(3个或3个以上),则采用“正交分解法”。
一、单选题
1.如图所示,2022北京冬奥会冰壶比赛时某运动员将冰壶(可视为质点)以速度从栏线P沿虚线推出,假设冰壶沿虚线做匀减速直线运动,栏线P到营垒圆心O的距离是,营垒是由4个直径分别为和的同心圆组成。冰壶与冰面的动摩擦因数,运动员把冰壶推进直径是的圆内,重力加速度g取,则可能是( )
A. B.
C. D.
【答案】C
【解析】冰壶在冰面上沿虚线做减速直线运动,把冰壶推进直径是的圆内,冰壶匀减速运动到0的位移
也就是位移满足
加速度大小
根据运动学公式
代入数据得
故选C。
2.中欧班列在欧亚大陆开辟了“生命之路”,为国际抗疫贡献了中国力量。某运送防疫物资的班列由40节质量相等的车厢组成,在车头牵引下,列车沿平直轨道匀加速行驶时,第2节对第3节车厢的牵引力为F。若每节车厢所受摩擦力、空气阻力均相等,则倒数第3节对倒数第2节车厢的牵引力为( )
A.F B. C. D.
【答案】C
【解析】根据题意可知第2节车厢对第3节车厢的牵引力为F,因为每节车厢质量相等,阻力相同,故第2节对第3节车厢根据牛顿第二定律有
设倒数第3节车厢对倒数第2节车厢的牵引力为F1,则根据牛顿第二定律有
联立解得。
故选C。
3.一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图像如图所示。乘客所受支持力的大小用FN表示,速度大小用v表示。重力加速度大小为g。以下判断正确的是( )
A.0~t1时间内,v增大,FN>mg B.t1~t2时间内,v减小,FN
【答案】D
【解析】A.由于s-t图像的斜率表示速度,可知在0~t1时间内速度增加,即乘客的加速度向下,处于失重状态,则FN
CD.在t2~t3时间内速度减小,即乘客的减速下降,超重,则FN>mg,选项C错误,D正确;
故选D。
4.如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是
A.小车静止时,,方向沿杆向上
B.小车静止时,,方向垂直杆向上
C.小车向右以加速度a运动时,一定有
D.小车向左以加速度a运动时,
【答案】D
【解析】当小车静止时,球处于平衡状态,则杆对小球的作用力F=mg,方向竖直向上.故AB错误.当小车向右以加速度a运动时,则球的合力为F合=ma,根据平行四边形定则知,杆对球的作用力F=,因为杆对球的作用力方向不一定沿杆,则作用力不一定等于.故C错误,D正确.故选D.
5.将一只皮球竖直向上抛出,皮球运动时受到空气阻力的大小与速度的大小成正比.下列描绘皮球在上升过程中加速度大小a与时间t关系的图象,可能正确的是
A. B.
C. D.
【答案】C
【解析】皮球竖直向上抛出,受到重力和向下的空气阻力,根据牛顿第二定律,有:,根据题意,空气阻力的大小与速度的大小成正比,有:,联立解得: ;由于速度不断减小,故加速度不断减小,到最高点速度为零,阻力为零,加速度为g,不为零,故BD均错误;根据,有,由于加速度减小,则也减小,也减小,即a-t图象的斜率不断减小,故A错误,C正确.
二、多选题
6.水平地面上有一质量为的长木板,木板的左端上有一质量为的物块,如图(a)所示。用水平向右的拉力F作用在物块上,F随时间t的变化关系如图(b)所示,其中、分别为、时刻F的大小。木板的加速度随时间t的变化关系如图(c)所示。已知木板与地面间的动摩擦因数为,物块与木板间的动摩擦因数为,假设最大静摩擦力均与相应的滑动摩擦力相等,重力加速度大小为g。则( )
A. B.
C. D.在时间段物块与木板加速度相等
【答案】BCD
【解析】A.图(c)可知,t1时滑块木板一起刚在从水平滑动,此时滑块与木板相对静止,木板刚要滑动,此时以整体为对象有
A错误;
BC.图(c)可知,t2滑块与木板刚要发生相对滑动,以整体为对象, 根据牛顿第二定律,有
以木板为对象,根据牛顿第二定律,有
解得
BC正确;
D.图(c)可知,0~t2这段时间滑块与木板相对静止,所以有相同的加速度,D正确。
故选BCD。
7.如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上。A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为。最大静摩擦力等于滑动摩擦力,重力加速度为g。现对A施加一水平拉力F,则( )
A.当时,A、B都相对地面静止
B.当时,A的加速度为
C.当时,A相对B滑动
D.无论F为何值,B的加速度不会超过
【答案】BCD
【解析】A.根据题意可知,B与地面间的最大静摩擦力为
因此要使B能够相对地面滑动,A对B所施加的摩擦力至少为
A、B间的最大静摩擦力为
故时,A、B都相对地面静止,A错误;
B.A、B恰好不相对滑动时,根据牛顿第二定律可知应当满足
且
即
则当≤F<3μmg,A、B将一起向右加速滑动。当时,对A和B整体受力分析有
解得
故B正确。
CD.当F≥3μmg时,A、B将以不同的加速度向右滑动,根据牛顿第二定律有
F-2μmg=2maA,
解得
,
故CD正确。
故选BCD。
8.如图所示,将两相同的木块a、b至于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁,开始时a、b均静止。弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力,b所受摩擦力,现将右侧细绳剪断,则剪断瞬间 ( )
A.大小不变 B.方向改变
C.仍然为零 D.方向向右
【答案】AD
【解析】初始状态,a在水平方向上受绳子拉力、弹簧的弹力还有摩擦力处于平衡,b受弹簧的弹力和绳子的拉力处于平衡,右侧细绳剪断的瞬间,弹簧的弹力不变,a仍然受三个力作用,摩擦力的大小和方向不变,而b受到向左的弹力,将受到向右的摩擦力,故选AD。
三、解答题
9.如图所示,一倾斜固定的传送带与水平面间夹角θ=37°,上下两端间距L=2.0m,传送带以v=1.0m/s的速率沿顺时针方向匀速运行。从距离传送带底端x0=1.0m的O点由静止释放一质量m=1.0kg的小滑块,滑块运动到传送带底端时与固定挡板P碰撞,碰撞时间极短且碰撞前后速率相等。滑块与传送带间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,取g=10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求:
(1)滑块与挡板P第一次碰撞时的速度大小v1;
(2)滑块与挡板P碰撞后离开挡板的最大距离xm;
(3)若滑块与挡板P第一次碰撞后立即在滑块上加一方向沿传送带斜向上、大小F=4.0N的恒力,一段时间后撤去。要使滑块能滑至传送带最上端,恒力持续作用的最短时间t。
【答案】(1)2m/s;(2)0.4m;(3)
【解析】(1)设滑块向下运动的加速度为a1,根据牛顿第二定律可得
由匀变速运动规律有
联立解得
v1=2m/s
(2)滑块第一次与挡板碰撞后速度大于传送带速度,滑块减速上滑,设碰后运动的加速度大小为a2,则
减速至与皮带速度相等时运动的距离为x1,则
之后滑块继续减速上滑至速度为零,加速度大小为a1,则
离开挡板的最大距离为
xm=x1+x2
联立解得
xm=0.4m
(3)滑块与挡板碰撞后,在恒力作用下的加速度大小设为a3,根据牛顿第二定律有
设该过程向上运动的距离为x3,运动时间为t1,则
解得
,
接着滑块向上匀速运动,最后撤去拉力再以a1向上减速,减速的距离应为x2,设匀
速运动的时间为t2,则
恒力持续作用的最短时间为
联立解得
10.如图,两个滑块A和B的质量分别为mA=1 kg和mB=5 kg,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4 kg,与地面间的动摩擦因数为μ2=0.1。某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3 m/s,A、B相遇时,A与木板恰好相对静止。设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10 m/s2,求:
(1)B与木板相对静止时,木板的速度;
(2)A、B开始运动时,两者之间的距离。
【答案】(1)1m/s;(2)1.9m。
【解析】(1)滑块A和B在木板上滑动时,木板也在地面上滑动,设A、B和木板所受的摩擦力大小分别为f1、f2和f3,A和B相对于地面的加速度大小分别是aA和aB,木板相对于地面的加速度大小为a1,在物块B与木板达到共同速度前有
①
②
③
由牛顿第二定律得
④
⑤
⑥
设在t1时刻,B与木板达到共同速度,设大小为v1。由运动学公式有
⑦
⑧
联立①②③④⑤⑥⑦⑧式,代入已知数据,可得B与木板相对静止时,木板的速度
⑨
(2)在t1时间间隔内,B相对于地面移动的距离为
⑩
设在B与木板达到共同速度v1后,木板的加速度大小为a2,对于B与木板组成的体系,由牛顿第二定律有
由①②④⑤式知,aA=aB;再由⑦⑧可知,B与木板达到共同速度时,A的速度大小也为v1,但运动方向与木板相反;由题意知,A和B相遇时,A与木板的速度相同,设其大小为v2,设A的速度大小从v1变到v2所用时间为t2,则由运动学公式,对木板有
对A有
在t2时间间隔内,B(以及木板)相对地面移动的距离为
在(t1+t2)时间间隔内,A相对地面移动的距离为
A和B相遇时,A与木板的速度也恰好相同,因此A和B开始运动时,两者之间的距离为
联立以上各式,代入数据,A、B开始运动时,两者之间的距离
答:(1)B与木板相对静止时,木板的速度为1m/s;(2)A、B开始运动时,两者之间的距离为1.9m。
11.一长木板置于粗糙水平地面上,木板左端放置一小物块,在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示.时刻开始,小物块与木板一起以共同速度向右运动,直至时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的图线如图(b)所示.木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求
(1)木板与地面间的动摩擦因数及小物块与木板间的动摩擦因数;
(2)木板的最小长度;
(3)木板右端离墙壁的最终距离.
【答案】(1),;(2);(3)
【解析】(1)根据图像可以判定碰撞前木块与木板共同速度为
碰撞后木板速度水平向左,大小也是
木块受到滑动摩擦力而向右做匀减速,根据牛顿第二定律有
解得
木板与墙壁碰撞前,匀减速运动时间,位移,末速度
其逆运动则为匀加速直线运动可得
带入可得
木块和木板整体受力分析,滑动摩擦力提供合外力,即
可得
(2)碰撞后,木板向左匀减速,依据牛顿第二定律有
可得
对滑块,则有加速度
滑块速度先减小到0,此时碰后时间为
此时,木板向左的位移为末速度
滑块向右位移
此后,木块开始向左加速,加速度仍为
木块继续减速,加速度仍为
假设又经历二者速度相等,则有
解得
此过程,木板位移末速度
滑块位移
此后木块和木板一起匀减速.
二者的相对位移最大为
滑块始终没有离开木板,所以木板最小的长度为
(3)最后阶段滑块和木板一起匀减速直到停止,整体加速度
位移
所以木板右端离墙壁最远的距离为
12.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为m的小物块a相连,如图所示。质量为的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0,从t=0时开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。求:
(1)弹簧的劲度系数;
(2)物块b加速度的大小;
(3)在物块a、b分离前,外力大小随时间变化的关系式。
【答案】(1) (2) (3)
【解析】 (1)对整体分析,根据平衡条件可知,沿斜面方向上重力的分力与弹簧弹力平衡,则有:
kx0=(m+ m)gsinθ
解得
k=
(2)由题意可知,b经两段相等的时间位移为x0;
由匀变速直线运动相邻相等时间内位移关系的规律可知
说明当形变量为时二者分离;
对m分析,因分离时ab间没有弹力,则根据牛顿第二定律可知
kx1-mgsinθ=ma
联立解得
a=
(3)设时间为t,则经时间t时,ab前进的位移
x=at2=
则形变量变为
△x=x0-x
对整体分析可知,由牛顿第二定律有
F+k△x-(m+m)gsinθ=(m+m)a
解得
F= mgsinθ+t2
因分离时位移x=由
x==at2
解得
故应保证0≤t<,F表达式才能成立。
13.如图甲所示,质量为2kg的木板B静止在水平面上.某时刻物块A(可视为质点)从木板的左侧沿木板上表面滑上木板,初速度v0=4m/s.此后A和B运动的v-t图象如图乙所示,取重力加速度g=10m/s2,求:
(1)A与B上表面之间的动摩擦因数μ1;
(2)B与水平面间的动摩擦因数μ2;
(3)A的质量.
【答案】(1)0.2 (2)0.1 (3)6kg
【解析】A滑上B做匀减速直线运动,根据速度时间图线得出匀减速运动的加速度大小,根据牛顿第二定律求出A与B之间的动摩擦因数;A、B速度相同后,一起做匀减速运动,根据速度时间图线求出匀减速运动的加速度大小,结合牛顿第二定律求出与水平面间的动摩擦因数;隔离对M分析,根据速度时间图线得出B的加速度,根据牛顿第二定律求出A的质量.
(1)由图象可知,A在0~1 s内的加速度
对A由牛顿第二定律得,-μ1mg=ma1
解得:μ1=0.2
(2)由图象知,A、B在1~3 s内的加速度
对A、B整体由牛顿第二定律得:-(M+m)gμ2=(M+m)a3
解得:μ2=0.1
(3)由图象可知B在0~1 s内的加速度
对B由牛顿第二定律得,μ1mg-μ2(M+m)g=Ma2
代入数据解得:m=6 kg
14.如图所示,一沿水平方向做匀加速直线运动的车厢中,悬挂小球的悬线偏离竖直方向的夹角,小球和车厢相对静止,小球的质量为,取,,,求:
(1)车厢运动的加速度;
(2)悬线对小球的拉力大小.
【答案】(1),方向水平向右(2)12.5N
【解析】解法一 矢量合成法
(1)选小球为研究对象,对其进行受力分析如图所示,有
又由牛顿第二定律得
则小球的加速度大小为
小球和车厢相对静止,故车厢的加速度大小也为,方向水平向右.
(2)悬线对小球的拉力大小为
.
解法二 正交分解法
建立直角坐标系,并将悬线对小球的拉力正交分解,因小球和车厢相对静止,则沿水平方向有
(为车厢的加速度)
沿竖直方向有
联立以上两式得, ,的方向水平向右.
车厢的加速度大小也为,方向水平向右.
