6.3.1二项式定理2 课件(共14张PPT)
文档属性
| 名称 | 6.3.1二项式定理2 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 11:59:54 | ||
图片预览



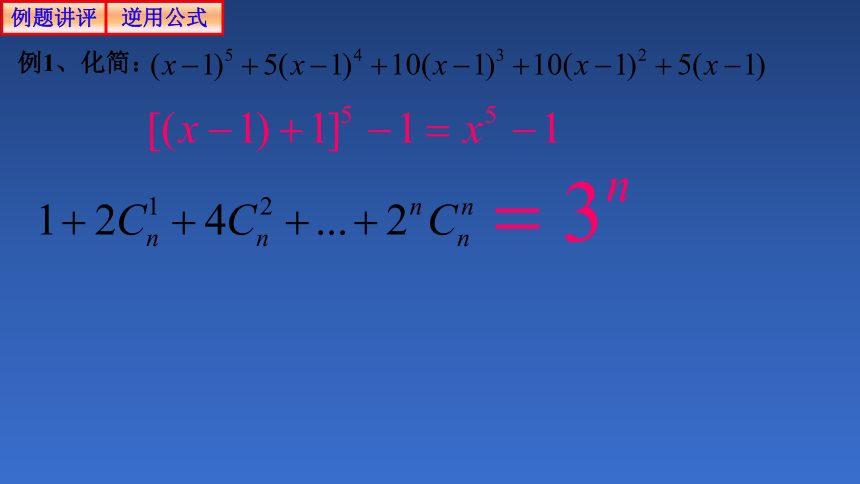



文档简介
(共14张PPT)
6.3.1二项式定理(二)
1.二项式定理是什么?二项展开式有哪些基本特征?
(3) 各项的二项式系数依次为,,,…,, 且与a,b无关.
温故而知新
二项展开式有以下特征:
(1)共有n+1项。
(2)各项里a的指数从n起依次减小1,直到0为止;b的指数从0起依次增加1,直到n为止。每一项里a、b的指数和均为n。
(a+b)n=an+an-1b+an-2b2+…+abn-1+ bn
2.二项展开式的通项是什么?
解:
(1)
(2)
(3)
巩固练习
例1、化简:
例题讲评
逆用公式
【思路点拨】 可先借助通项公式,利用第6项为常数项求n,然后再根据通项公式即可求得(2)、(3).
例题讲评
例题讲评
求展开式中特定项
学习新知
对于常数项,隐含条件是字母的指数为0(即0次项); 对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.
若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.另外,在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
思维总结
例3、若 展开式中前三项系数成等差数列,
求(1)展开式中含x的一次幂的项;
(2)展开式中系数最大的项。
练习: 的展开式中,无理项的个数是( )
A .83 B.84 C.85 D.86
B
例题讲评
解:
所以,展开式的常数项为
例题讲评
例5.
解:
例题讲评
2.已知 的第5项的二项式系数与第3 项的二项式系数比
为14:3,求展开式中不含x 的项。
3.已知 的展开式中,第5项的系数与第3 项的系数比为
56:3,求展开式中的常数项。
1、已知 展开式中第2项大于它的相邻两项,求x的范围。
巩固练习
1、求 的展开式中的 系数.
2、求 展开式中的常数项.
提高练习
A.10 B.20 C.30 D.40
1.二项式定理:
2.通项:
3.二项式系数:
第(r+1)项
4.特殊地:
注:项的系数与二项式系数是两个不同的概念
令以x=1得
课堂小结
6.3.1二项式定理(二)
1.二项式定理是什么?二项展开式有哪些基本特征?
(3) 各项的二项式系数依次为,,,…,, 且与a,b无关.
温故而知新
二项展开式有以下特征:
(1)共有n+1项。
(2)各项里a的指数从n起依次减小1,直到0为止;b的指数从0起依次增加1,直到n为止。每一项里a、b的指数和均为n。
(a+b)n=an+an-1b+an-2b2+…+abn-1+ bn
2.二项展开式的通项是什么?
解:
(1)
(2)
(3)
巩固练习
例1、化简:
例题讲评
逆用公式
【思路点拨】 可先借助通项公式,利用第6项为常数项求n,然后再根据通项公式即可求得(2)、(3).
例题讲评
例题讲评
求展开式中特定项
学习新知
对于常数项,隐含条件是字母的指数为0(即0次项); 对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.
若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.另外,在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
思维总结
例3、若 展开式中前三项系数成等差数列,
求(1)展开式中含x的一次幂的项;
(2)展开式中系数最大的项。
练习: 的展开式中,无理项的个数是( )
A .83 B.84 C.85 D.86
B
例题讲评
解:
所以,展开式的常数项为
例题讲评
例5.
解:
例题讲评
2.已知 的第5项的二项式系数与第3 项的二项式系数比
为14:3,求展开式中不含x 的项。
3.已知 的展开式中,第5项的系数与第3 项的系数比为
56:3,求展开式中的常数项。
1、已知 展开式中第2项大于它的相邻两项,求x的范围。
巩固练习
1、求 的展开式中的 系数.
2、求 展开式中的常数项.
提高练习
A.10 B.20 C.30 D.40
1.二项式定理:
2.通项:
3.二项式系数:
第(r+1)项
4.特殊地:
注:项的系数与二项式系数是两个不同的概念
令以x=1得
课堂小结
