6.3.2二项式系数的性质 课件(共16张PPT)
文档属性
| 名称 | 6.3.2二项式系数的性质 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 459.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 21:07:03 | ||
图片预览





文档简介
(共16张PPT)
6.3.2二项式系数的性质
1.二项式定理是什么?二项展开式有哪些基本特征?
(3) 各项的二项式系数依次为 且与a,b无关.
温故而知新
(1)共有n+1项。
(2)各项里a的指数从n起依次减小1,直到0为止;b的指数从0起依次增加1,直到n为止。每一项里a、b的指数和均为n。
2.二项展开式的通项是什么?
3.组合数有哪两个基本性质?
二项展开式有以下特征:
杨辉三角
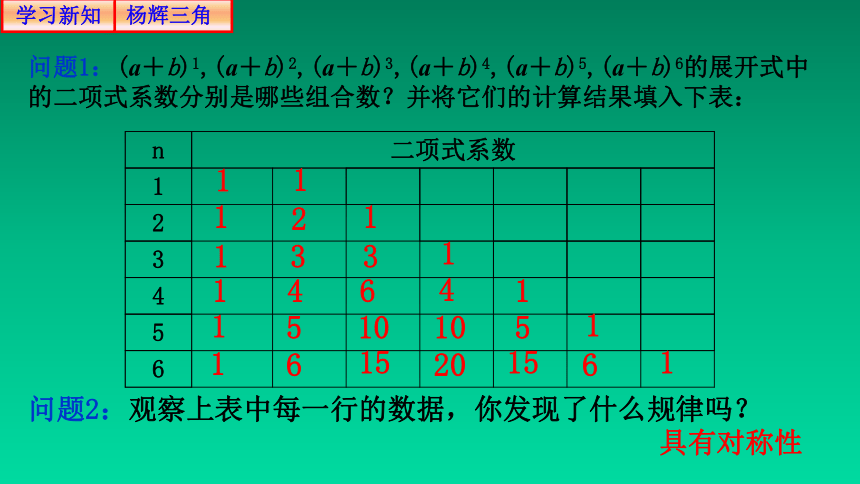
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
15
20
6
学习新知
问题2:观察上表中每一行的数据,你发现了什么规律吗?
具有对称性
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
问题3:将上表写成如下形式,你又能发现这些数据有什么新的规律吗
学习新知
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
(3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
学习新知
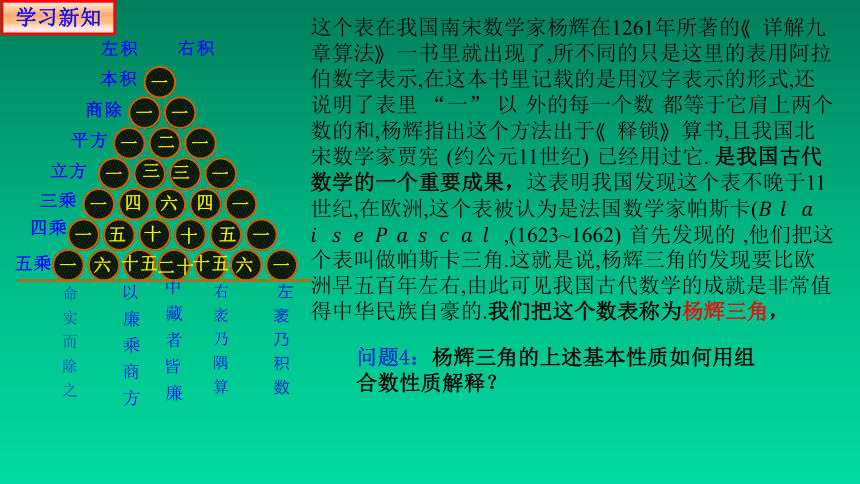
这个表在我国南宋数学家杨辉在1261年所著的 详解九章算法 一书里就出现了,所不同的只是这里的表用阿拉伯数字表示,在这本书里记载的是用汉字表示的形式,还说明了表里 “一” 以 外的每一个数 都等于它肩上两个数的和,杨辉指出这个方法出于 释锁 算书,且我国北宋数学家贾宪 (约公元11世纪) 已经用过它. 是我国古代数学的一个重要成果,这表明我国发现这个表不晚于11世纪,在欧洲,这个表被认为是法国数学家帕斯卡( ,(1623~1662) 首先发现的 ,他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.我们把这个数表称为杨辉三角,
问题4:杨辉三角的上述基本性质如何用组合数性质解释?
二项式系数的性质
问题1:对给定的正整数n,设函数 ,
r∈{0,1,2,…,n},
当n=6时,函数f(r)的图象是什么?
学习新知
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
问题2:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
问题3:在二项式系数
中,哪些二项式系数是相等的?
与首末两端“等距离”的两个二项式系数相等.
学习新知
问题4:相邻两个二项式系数的大小关系如何?从理论上如何确定 与 的大小?
问题5:通过上述分析,二项式系数的增减性与最大值分别是什么?
二项式系数的前半部分是递增的,后半部分是递减的,且在中间取得最大值.
学习新知
问题6:当n分别为偶数和奇数时,第几项的二项式系数最大?
当n为偶数时,第 项的二项式系数 为最大;
当n为奇数时,第 的二项式系数 和第 项的
二项式系数 相等,且同时为最大.
学习新知
问题7:在二项式定理中,a,b可以任意取值,特别地,当a=b=1时,可得什么结论?
例1:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
性质三:二项式系数之和
因此,我们可以通过对a,b适当赋值来得到上述两个系数和。
典型例题
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
即
问题8:上述结果表明,所有二项式系数之和等于2n,所有奇数项的二项式系数之和与所有偶数项的二项式系数之和相等,且都等于2n-1.那么,如何求(3+2x)n的展开式中各项的系数之和?
令x=1,得各项的系数之和为5n.
学习新知
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
巩固练习
a+b
126
21
例1 填空:
(1)(x-y)11的展开式中系数最大的项第 项,系数最小的项第 项;
(2) ,
7
6
1023
512
典型例题
例2 已知(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项.
例3 求集合A={a1,a2,…,an}共有多少个子集?
典型例题
例4、已知(1-2x)7=a0+ a1x + a2x2 + …+ a7x7 ,则
(1)a1+a2+a3+…+a7=_______
(2)a1+a3+a5+a7 =_________
(3)a0+a2+a4+a6 =_________
赋值法
练习:
若已知(1+2x)200= a0+ a1(x-1) + a2(x-1)2 + …+ a200(x-1)200
求a1+a3+a5+a7+…+a199的值。
例题讲评
2
1093
-1094
一般地, 展开式的二项式系 有如下性质:
(1)
(2)
(4)
(3)当n为偶数时, 最大
当n为奇数时, = 且最大
(对称性)
课堂小结
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
课堂小结
1.杨辉三角反映了二项式系数的变化规律,其理论依据是组合数的两个性质.杨辉三角中还有许多有趣性质,可作为一个研究性课题进行探究.
2.二项式系数的性质实质是组合数的一些性质,常作为解决组合数问题的理论依据,但这些性质不能类推到二项展开式的系数.
3.令x=1,可求得(a+bx)n的展开式中各项的系数之和,当x取其它值时,还可以得出一些相关结论,这是一种赋值的方法.
6.3.2二项式系数的性质
1.二项式定理是什么?二项展开式有哪些基本特征?
(3) 各项的二项式系数依次为 且与a,b无关.
温故而知新
(1)共有n+1项。
(2)各项里a的指数从n起依次减小1,直到0为止;b的指数从0起依次增加1,直到n为止。每一项里a、b的指数和均为n。
2.二项展开式的通项是什么?
3.组合数有哪两个基本性质?
二项展开式有以下特征:
杨辉三角
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
15
20
6
学习新知
问题2:观察上表中每一行的数据,你发现了什么规律吗?
具有对称性
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
问题3:将上表写成如下形式,你又能发现这些数据有什么新的规律吗
学习新知
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
(3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
学习新知
这个表在我国南宋数学家杨辉在1261年所著的 详解九章算法 一书里就出现了,所不同的只是这里的表用阿拉伯数字表示,在这本书里记载的是用汉字表示的形式,还说明了表里 “一” 以 外的每一个数 都等于它肩上两个数的和,杨辉指出这个方法出于 释锁 算书,且我国北宋数学家贾宪 (约公元11世纪) 已经用过它. 是我国古代数学的一个重要成果,这表明我国发现这个表不晚于11世纪,在欧洲,这个表被认为是法国数学家帕斯卡( ,(1623~1662) 首先发现的 ,他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.我们把这个数表称为杨辉三角,
问题4:杨辉三角的上述基本性质如何用组合数性质解释?
二项式系数的性质
问题1:对给定的正整数n,设函数 ,
r∈{0,1,2,…,n},
当n=6时,函数f(r)的图象是什么?
学习新知
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
问题2:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
问题3:在二项式系数
中,哪些二项式系数是相等的?
与首末两端“等距离”的两个二项式系数相等.
学习新知
问题4:相邻两个二项式系数的大小关系如何?从理论上如何确定 与 的大小?
问题5:通过上述分析,二项式系数的增减性与最大值分别是什么?
二项式系数的前半部分是递增的,后半部分是递减的,且在中间取得最大值.
学习新知
问题6:当n分别为偶数和奇数时,第几项的二项式系数最大?
当n为偶数时,第 项的二项式系数 为最大;
当n为奇数时,第 的二项式系数 和第 项的
二项式系数 相等,且同时为最大.
学习新知
问题7:在二项式定理中,a,b可以任意取值,特别地,当a=b=1时,可得什么结论?
例1:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
性质三:二项式系数之和
因此,我们可以通过对a,b适当赋值来得到上述两个系数和。
典型例题
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
即
问题8:上述结果表明,所有二项式系数之和等于2n,所有奇数项的二项式系数之和与所有偶数项的二项式系数之和相等,且都等于2n-1.那么,如何求(3+2x)n的展开式中各项的系数之和?
令x=1,得各项的系数之和为5n.
学习新知
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
巩固练习
a+b
126
21
例1 填空:
(1)(x-y)11的展开式中系数最大的项第 项,系数最小的项第 项;
(2) ,
7
6
1023
512
典型例题
例2 已知(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项.
例3 求集合A={a1,a2,…,an}共有多少个子集?
典型例题
例4、已知(1-2x)7=a0+ a1x + a2x2 + …+ a7x7 ,则
(1)a1+a2+a3+…+a7=_______
(2)a1+a3+a5+a7 =_________
(3)a0+a2+a4+a6 =_________
赋值法
练习:
若已知(1+2x)200= a0+ a1(x-1) + a2(x-1)2 + …+ a200(x-1)200
求a1+a3+a5+a7+…+a199的值。
例题讲评
2
1093
-1094
一般地, 展开式的二项式系 有如下性质:
(1)
(2)
(4)
(3)当n为偶数时, 最大
当n为奇数时, = 且最大
(对称性)
课堂小结
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
课堂小结
1.杨辉三角反映了二项式系数的变化规律,其理论依据是组合数的两个性质.杨辉三角中还有许多有趣性质,可作为一个研究性课题进行探究.
2.二项式系数的性质实质是组合数的一些性质,常作为解决组合数问题的理论依据,但这些性质不能类推到二项展开式的系数.
3.令x=1,可求得(a+bx)n的展开式中各项的系数之和,当x取其它值时,还可以得出一些相关结论,这是一种赋值的方法.
