7.1.1条件概率 课件(共26张PPT)
文档属性
| 名称 | 7.1.1条件概率 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
7.1.1 条件概率
复习引入
彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验,它们具有如下共同特征;
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
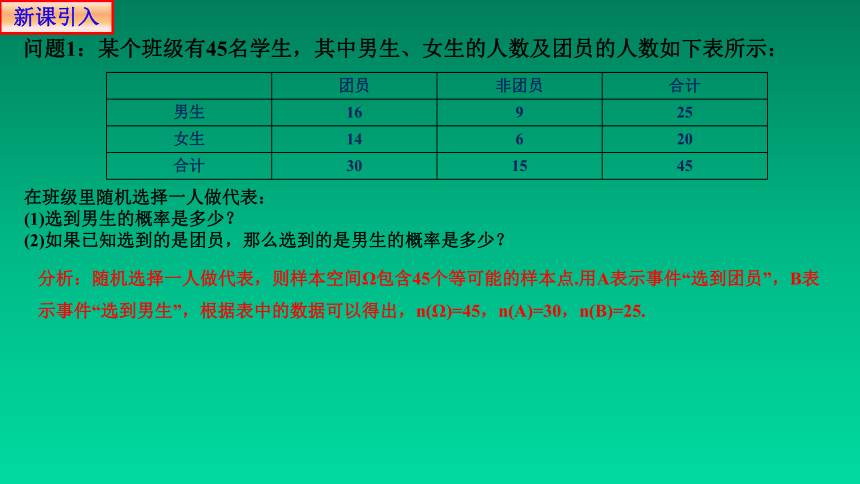
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
新课引入
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
新课引入
解:(1)根据古典概型知识可知,选到男生的概率
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
你能算吗?
新课引入
某日你妈妈带你到她的一个朋友家做客,闲谈间正巧碰到她的女儿回家,这时主人介绍说:“这是我的一个女儿,我还有一个孩子呢。”这个家庭中有两个孩子,已知其中有一个是女孩,问这时另一个孩子也是女孩的概率为多大?
问题2 : 这个家庭中有两个孩子,已知其中有一个是女孩,问这时另一个小孩也是女孩的概率为多大?
解:
“在家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时A成为样本空间,事件B就是积事件AB.根据古典概型知识可知,
在上面两个问题中,在事件A发生的条件下,事件B发生的概率都是
问题变式: 这个家庭中有两个孩子,已知老大是女孩,问这时另一个小孩也是女孩的概率为多大?
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
1、定义
条件概率 Conditional Probability
一般把 P(B|A)读作 A 发生的条件下 B 的概率。
学习新知
2条件概率的性质:
(通常适用古典概率模型)
(适用于一般的概率模型)
学习新知
学习新知
条件概率与事件独立性的关系
问题3:在问题1和问题2中,都有P(B|A)≠P(B).一般地, P(B|A)与P(B)不一定相等。如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件?
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,
这等价于P(B|A)=P(B)成立.
=
思考:对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式(multiplication formula).
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的 题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
典型例题
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”。
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即。
因为n(AB)=
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率。显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,
这时还余下4道试题,其中代数题和几何题各2道.
因此,事件A发生的条件下,事件B发生的概率为
P(B|A)=
又P(A)= ,利用乘法公式可得
P(AB)=P(A) P(B|A)= =
某次数学考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,其中甲班10名同学中有4人及格,乙班10名同学有5人及格,现从两班10名同学中各抽取1人,已知有人及格,求乙班同学不及格的概率.
巩固练习
例2:已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
:用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关。
典型例题
例3: 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率。
解:(1)设Ai=“第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为A=A1UA2.
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P(A2)= P(A1)+P()P(A2|)=
因此,任意按最后1位数字,不超过2次就按对的概率为.
典型例题
(2)设B=“最后1位密码为偶数”,则P(A|B)=P(A1|B)+P(A2|B)== ;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
C
B
巩固练习
在某次外交谈判中,中外双方都为了自身的利益而互不相让,这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理,否则按中方的决议处理,假如你在现场,你会如何抉择?
B={出现的点数是奇数} ={1,3,5}
设A={出现的点数不超过3}={1,2,3}
只需求事件 A 发生的条件下,事件 B 的概率即P(B|A)
解法一(减缩样本空间法)
解1:
典型例题
2
1
3
4,6
5
解法2(条件概率定义法)
1.掷两颗均匀骰子,已知第一颗掷出6点条件下, 问“掷出点数之和不小于10”的概率是多少
解: 设A={掷出点数之和不小于10},B={第一颗掷出6点}
巩固练习
B
3.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则
所求概率为
0.56
0.7
5
巩固练习
一盒子装有4 只产品,其中有3 只一等品,1只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件A为“第一次取到的是一等品” ,事件B 为“第二次取到的是一等品”,试求条件概率P(B|A).
解
由条件概率的公式得
巩固练习
巩固练习
已知某产品的次品率为4%,其合格品中75%为一级品,则任选一件为一级品的概率为 ( )
A.75% B.96% C.72% D.78.125%
巩固练习
C
巩固练习
现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
1. 条件概率的定义.
课堂小结
2. 条件概率的性质.
3. 条件概率的计算方法.
(1)减缩样本空间法
(2)条件概率定义法
4.条件概率需注意以下几点
(1)事件B在事件A已发生这个附加条件下的概率与没有这个附加条件的概率是不同的.
(2)所谓条件概率,是当试验结果的一部分信息已知(即在原随机试验的条件下,再加上一定的条件),求另一事件在此条件下的概率.
(3)已知事件A发生,在此条件下B发生,相当于AB发生,求P(B|A)时,可把A看做新的基本事件空间来计算B发生的概率,
课堂小结
5.如何理解条件概率公式?
(1)前提条件:P(A)>0
(2)条件概率公式揭示了条件概率P(B|A)与事件P(A),P(AB)三者之间的关系,由条件概率公式可以解决下列两类问题.
①已知P(A),P(AB),求P(B|A);
②已知P(A),P(B|A),求P(AB).
课堂小结
课堂小结
送给同学们一段话:
在概率的世界里充满着和我们直觉截然不同的事物。面对表象同学们要坚持实事求是的态度、锲而不舍的精神。尽管我们的学习生活充满艰辛,但我相信只要同学们不断进取、挑战自我,我们一定会达到成功的彼岸!
7.1.1 条件概率
复习引入
彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验,它们具有如下共同特征;
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
新课引入
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
新课引入
解:(1)根据古典概型知识可知,选到男生的概率
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
你能算吗?
新课引入
某日你妈妈带你到她的一个朋友家做客,闲谈间正巧碰到她的女儿回家,这时主人介绍说:“这是我的一个女儿,我还有一个孩子呢。”这个家庭中有两个孩子,已知其中有一个是女孩,问这时另一个孩子也是女孩的概率为多大?
问题2 : 这个家庭中有两个孩子,已知其中有一个是女孩,问这时另一个小孩也是女孩的概率为多大?
解:
“在家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).此时A成为样本空间,事件B就是积事件AB.根据古典概型知识可知,
在上面两个问题中,在事件A发生的条件下,事件B发生的概率都是
问题变式: 这个家庭中有两个孩子,已知老大是女孩,问这时另一个小孩也是女孩的概率为多大?
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
1、定义
条件概率 Conditional Probability
一般把 P(B|A)读作 A 发生的条件下 B 的概率。
学习新知
2条件概率的性质:
(通常适用古典概率模型)
(适用于一般的概率模型)
学习新知
学习新知
条件概率与事件独立性的关系
问题3:在问题1和问题2中,都有P(B|A)≠P(B).一般地, P(B|A)与P(B)不一定相等。如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件?
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,
这等价于P(B|A)=P(B)成立.
=
思考:对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式(multiplication formula).
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的 题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
典型例题
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”。
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即。
因为n(AB)=
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率。显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,
这时还余下4道试题,其中代数题和几何题各2道.
因此,事件A发生的条件下,事件B发生的概率为
P(B|A)=
又P(A)= ,利用乘法公式可得
P(AB)=P(A) P(B|A)= =
某次数学考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,其中甲班10名同学中有4人及格,乙班10名同学有5人及格,现从两班10名同学中各抽取1人,已知有人及格,求乙班同学不及格的概率.
巩固练习
例2:已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
:用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关。
典型例题
例3: 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率。
解:(1)设Ai=“第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为A=A1UA2.
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P(A2)= P(A1)+P()P(A2|)=
因此,任意按最后1位数字,不超过2次就按对的概率为.
典型例题
(2)设B=“最后1位密码为偶数”,则P(A|B)=P(A1|B)+P(A2|B)== ;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
C
B
巩固练习
在某次外交谈判中,中外双方都为了自身的利益而互不相让,这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理,否则按中方的决议处理,假如你在现场,你会如何抉择?
B={出现的点数是奇数} ={1,3,5}
设A={出现的点数不超过3}={1,2,3}
只需求事件 A 发生的条件下,事件 B 的概率即P(B|A)
解法一(减缩样本空间法)
解1:
典型例题
2
1
3
4,6
5
解法2(条件概率定义法)
1.掷两颗均匀骰子,已知第一颗掷出6点条件下, 问“掷出点数之和不小于10”的概率是多少
解: 设A={掷出点数之和不小于10},B={第一颗掷出6点}
巩固练习
B
3.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则
所求概率为
0.56
0.7
5
巩固练习
一盒子装有4 只产品,其中有3 只一等品,1只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件A为“第一次取到的是一等品” ,事件B 为“第二次取到的是一等品”,试求条件概率P(B|A).
解
由条件概率的公式得
巩固练习
巩固练习
已知某产品的次品率为4%,其合格品中75%为一级品,则任选一件为一级品的概率为 ( )
A.75% B.96% C.72% D.78.125%
巩固练习
C
巩固练习
现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
1. 条件概率的定义.
课堂小结
2. 条件概率的性质.
3. 条件概率的计算方法.
(1)减缩样本空间法
(2)条件概率定义法
4.条件概率需注意以下几点
(1)事件B在事件A已发生这个附加条件下的概率与没有这个附加条件的概率是不同的.
(2)所谓条件概率,是当试验结果的一部分信息已知(即在原随机试验的条件下,再加上一定的条件),求另一事件在此条件下的概率.
(3)已知事件A发生,在此条件下B发生,相当于AB发生,求P(B|A)时,可把A看做新的基本事件空间来计算B发生的概率,
课堂小结
5.如何理解条件概率公式?
(1)前提条件:P(A)>0
(2)条件概率公式揭示了条件概率P(B|A)与事件P(A),P(AB)三者之间的关系,由条件概率公式可以解决下列两类问题.
①已知P(A),P(AB),求P(B|A);
②已知P(A),P(B|A),求P(AB).
课堂小结
课堂小结
送给同学们一段话:
在概率的世界里充满着和我们直觉截然不同的事物。面对表象同学们要坚持实事求是的态度、锲而不舍的精神。尽管我们的学习生活充满艰辛,但我相信只要同学们不断进取、挑战自我,我们一定会达到成功的彼岸!
