7.2离散型随机变量及其分布列2 课件(共21张PPT)
文档属性
| 名称 | 7.2离散型随机变量及其分布列2 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 694.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 21:14:19 | ||
图片预览








文档简介
(共21张PPT)
离散型随机变量的分布列
随着试验结果变化而变化的变量称为随机变量,常用大写英文字母X,Y,Z…表示。
1、随机变量定义
2、随机变量的分类
①离散型随机变量:
X的取值可一、一列出
②连续型随机变量:
X可以取某个区间内的一切值
3、古典概型:
①试验中所有可能出现的基本事件只有有限个;
②每个基本事件出现的可能性相等。
复习引入
X
1
2
6
5
4
3
该表不仅列出了随机变量X的所有取值而且列出了X的每一个取值的概率.
列成表的形式
思考:抛掷一枚骰子,所得的点数X有哪些值?取每个值的概率是多少?
X可能的取值有1,2,3,4,5,6
学习新知
离散型随机变量的分布列
为随机变量X的概率分布列,简称X的分布列。
我们称X取每一个值 ( =1,2, )的概率 ( = )= ,i=1,2,3 xn
设离散型随机变量X可能取的值为
1、概率分布列(分布列)
学习新知
离散型随机变量的分布列具有下述两个性质:
注意:①.列出随机变量的所有可能取值;
②.求出随机变量的每一个值发生的概率.
求随机变量X的分布列的步骤如下:
(1).确定 X 的可能取值 xi ;
(2).求出相应的概率 P=(X=xi)= pi ;
(3).列成表格的形式.
学习新知
抛掷一枚骰子,向上一面的点数是一个随机变量X其可能取的值是 ;它取各个不同值的概率都等于________.
1,2,3,4,5,6
离散型随机变量分布列的变化情况可以用图象表示.如在掷骰子试验中,掷出的点数X的分布列在直角坐标系中的图象如图所示.
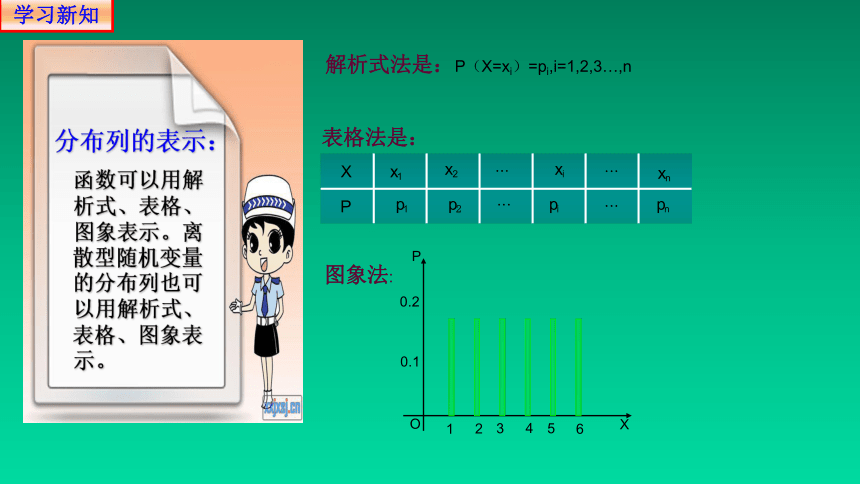
函数可以用解析式、表格、图象表示。离散型随机变量的分布列也可以用解析式、表格、图象表示。
解析式法是:P(X=xi)=pi,i=1,2,3…,n
表格法是:
图象法:
分布列的表示:
学习新知
一般地,离散型随机变量在某一范围内的概率等于它取这个范围内各个值的概率之和。
例1、某一射手射击所得环数的分布列如下:
ξ 4 5 6 7 8 9 10
p 0.02 0.04 0.06 0.09 0.28 0.29 0.22
求此射手“射击一次命中环数≥7”的概率
典型例题
例2.从标有数字1,2,3,4,5,6的6张卡片中任取2张,所取卡片上的数字之和的概率分布列.
设所取卡片上的数字之和为X,则X=3,4,5,…,11.
X=3,表示取出标有1,2的两张卡片;
X=4,表示取出标有1,3的两张卡片;
X=5,表示取出标有2,3或1,4的两张卡片;
X=6,表示取出标有2,4或1,5的两张卡片;
X=7,表示取出标有3,4或2,5或1,6的两张卡片;
X=8,表示取出标有2,6或3,5的两张卡片;
X=9,表示取出标有3,6或4,5的两张卡片;
X=10,表示取出标有4,6的两张卡片;
X=11,表示取出标有5,6的两张卡片.
从标有数字1,2,3,4,5,6的6张卡片中任取2张,所取卡片上的数字之和的概率分布列.
随机变量X的分布列为
X -1 0 1 2 3
p 0.16 a/10 a2 a/5 0.3
求常数a。
解:由离散型随机变量的分布列的性质有
解得:
(舍)或
巩固练习
例3.在掷一枚图钉的随机试验中,令
如果尖向上的概率为p,试写出随机变量X的分布列
解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:
X 0 1
P 1—p p
例题讲评
解:
X 0 1
P 0.95 0.05
例4.一批产品中次品率为5%,随机抽取1件,定义
X 0 1
P 1-P P
两点分布列
学习新知
对于只有两个可能结果的随机试验,用 表示“成功”,
表示“失败”,定义
X 2 3
P 0.3 0.7
思考:随机变量X的分布列由下表给出,它服从两点分布吗
注: 只取两个不同值的随机变量并不一定服从两点分布
不服从两点分布,因为X的取值不是0或1
例5.某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如下表所示.
等级 不及格 及格 中等 良好 优秀
分数 1 2 3 4 5
人数 20 50 60 40 30
解:
X 1 2 3 4 5
例题讲评
从这200名学生中任意选取1人,求所选同学分数 的分布列以及 ( ≥4).
由题意知, 是一个离散型随机变量,其可能取值为1,2,3,4,5,且{ =1}=“不及格”,{ =2}=“及格”,
根据古典概型的知识,可得 的分布列
例6 一批笔记本电脑共有10台,其中A品牌3台 ,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
例题讲评
解:设挑选的2台电脑中 品牌的台数为 ,则 的可能取值为0,1,2.根据古典概型的知识,可得 的分布列
一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以X表示取出的3个球中的最小号码,试写出X的分布列.
解: 随机变量X的可取值为 1,2,3.
当X=1时,即取出的三只球中的最小号码为1,则其它两只球只能在编号为2,3,4,5的四只球中任取两只,故有P(X=1)= =3/5;
同理可得P(X=2)=3/10;P(X=3)=1/10.
因此,X的分布列如下表所示
X 1 2 3
p 3/5 3/10 1/10
巩固练习
1、下列A、B、C、D四个表,其中能成为随机变量X的分布列的是( )
A
X 0 1
P 0.6 0.3
B
X 0 1 2
P 0 0.8 0.2
C
D
B
X 1 2 3
P 0.5 0.4 0.2
X -1 1 2
P 0.5 0.8 -0.3
2.设随机变量ξ的分布列如下:
则a的值为 .
3.设随机变量ξ的分布列:
巩固练习
1、在射击的随机试验中,令X= 如
果射中的概率为0.8,求随机变量X的分布列.
0,射中,
1,未射中
2、设某项试验的成功率是失败率的2倍,用随机变量X去描述1次试验的成功次数,则失败率p等于( )
A.0 B. C. D.
C
巩固练习
X 0 1
P 0.8 0.2
例6.已知随机变量X的分布列如下:
X
-2
-1
3
2
1
0
分别求出随机变量⑴Y1= X
(2)Y2= X2的分布列.
例题讲评
解:
且相应取值的概率没有变化
∴Y1的分布列为:
Y1
P
-1
1
0
⑴由
可得Y1
的取值为
,0,
,1,
例6.已知随机变量X的分布列如下:
X
-2
-1
3
2
1
0
分别求出随机变量⑴Y1= X
(2)Y2= X2的分布列.
解:
∴
Y2的分布列为:
⑵由Y2= X2可得Y2的取值为0、1、4、9
0
9
4
1
例题讲评
一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以X表示取出的3个球中的最小号码,试写出X的分布列.
解: 随机变量X的可取值为 1,2,3.
当X=1时,即取出的三只球中的最小号码为1,则其它两只球只能在编号为2,3,4,5的四只球中任取两只,故有P(X=1)= =3/5;
同理可得 P(X=2)=3/10;P(X=3)=1/10.
因此,X 的分布列如下表所示
X 1 2 3
P 3/5 3/10 1/10
注:在写出X的分布列后,要及时检查所有的概率之和是否为1.
巩固练习
分布列的概念:
课堂小结
上表称为离散型随机变量 的概率分布列,简称为 的分布列.有时为了表达简单,也用等式 ( = )= , =1,2, , 表示 的分布列.
求分布列的步骤:
(1)找出随机变量X的所有可能的取值
(2)求出各取值的概率P(X=xi)=Pi
(3)列成表格。
1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单问题;
3 、两点分布
4 、超几何分布
课堂小结
离散型随机变量的分布列
随着试验结果变化而变化的变量称为随机变量,常用大写英文字母X,Y,Z…表示。
1、随机变量定义
2、随机变量的分类
①离散型随机变量:
X的取值可一、一列出
②连续型随机变量:
X可以取某个区间内的一切值
3、古典概型:
①试验中所有可能出现的基本事件只有有限个;
②每个基本事件出现的可能性相等。
复习引入
X
1
2
6
5
4
3
该表不仅列出了随机变量X的所有取值而且列出了X的每一个取值的概率.
列成表的形式
思考:抛掷一枚骰子,所得的点数X有哪些值?取每个值的概率是多少?
X可能的取值有1,2,3,4,5,6
学习新知
离散型随机变量的分布列
为随机变量X的概率分布列,简称X的分布列。
我们称X取每一个值 ( =1,2, )的概率 ( = )= ,i=1,2,3 xn
设离散型随机变量X可能取的值为
1、概率分布列(分布列)
学习新知
离散型随机变量的分布列具有下述两个性质:
注意:①.列出随机变量的所有可能取值;
②.求出随机变量的每一个值发生的概率.
求随机变量X的分布列的步骤如下:
(1).确定 X 的可能取值 xi ;
(2).求出相应的概率 P=(X=xi)= pi ;
(3).列成表格的形式.
学习新知
抛掷一枚骰子,向上一面的点数是一个随机变量X其可能取的值是 ;它取各个不同值的概率都等于________.
1,2,3,4,5,6
离散型随机变量分布列的变化情况可以用图象表示.如在掷骰子试验中,掷出的点数X的分布列在直角坐标系中的图象如图所示.
函数可以用解析式、表格、图象表示。离散型随机变量的分布列也可以用解析式、表格、图象表示。
解析式法是:P(X=xi)=pi,i=1,2,3…,n
表格法是:
图象法:
分布列的表示:
学习新知
一般地,离散型随机变量在某一范围内的概率等于它取这个范围内各个值的概率之和。
例1、某一射手射击所得环数的分布列如下:
ξ 4 5 6 7 8 9 10
p 0.02 0.04 0.06 0.09 0.28 0.29 0.22
求此射手“射击一次命中环数≥7”的概率
典型例题
例2.从标有数字1,2,3,4,5,6的6张卡片中任取2张,所取卡片上的数字之和的概率分布列.
设所取卡片上的数字之和为X,则X=3,4,5,…,11.
X=3,表示取出标有1,2的两张卡片;
X=4,表示取出标有1,3的两张卡片;
X=5,表示取出标有2,3或1,4的两张卡片;
X=6,表示取出标有2,4或1,5的两张卡片;
X=7,表示取出标有3,4或2,5或1,6的两张卡片;
X=8,表示取出标有2,6或3,5的两张卡片;
X=9,表示取出标有3,6或4,5的两张卡片;
X=10,表示取出标有4,6的两张卡片;
X=11,表示取出标有5,6的两张卡片.
从标有数字1,2,3,4,5,6的6张卡片中任取2张,所取卡片上的数字之和的概率分布列.
随机变量X的分布列为
X -1 0 1 2 3
p 0.16 a/10 a2 a/5 0.3
求常数a。
解:由离散型随机变量的分布列的性质有
解得:
(舍)或
巩固练习
例3.在掷一枚图钉的随机试验中,令
如果尖向上的概率为p,试写出随机变量X的分布列
解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:
X 0 1
P 1—p p
例题讲评
解:
X 0 1
P 0.95 0.05
例4.一批产品中次品率为5%,随机抽取1件,定义
X 0 1
P 1-P P
两点分布列
学习新知
对于只有两个可能结果的随机试验,用 表示“成功”,
表示“失败”,定义
X 2 3
P 0.3 0.7
思考:随机变量X的分布列由下表给出,它服从两点分布吗
注: 只取两个不同值的随机变量并不一定服从两点分布
不服从两点分布,因为X的取值不是0或1
例5.某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如下表所示.
等级 不及格 及格 中等 良好 优秀
分数 1 2 3 4 5
人数 20 50 60 40 30
解:
X 1 2 3 4 5
例题讲评
从这200名学生中任意选取1人,求所选同学分数 的分布列以及 ( ≥4).
由题意知, 是一个离散型随机变量,其可能取值为1,2,3,4,5,且{ =1}=“不及格”,{ =2}=“及格”,
根据古典概型的知识,可得 的分布列
例6 一批笔记本电脑共有10台,其中A品牌3台 ,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
例题讲评
解:设挑选的2台电脑中 品牌的台数为 ,则 的可能取值为0,1,2.根据古典概型的知识,可得 的分布列
一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以X表示取出的3个球中的最小号码,试写出X的分布列.
解: 随机变量X的可取值为 1,2,3.
当X=1时,即取出的三只球中的最小号码为1,则其它两只球只能在编号为2,3,4,5的四只球中任取两只,故有P(X=1)= =3/5;
同理可得P(X=2)=3/10;P(X=3)=1/10.
因此,X的分布列如下表所示
X 1 2 3
p 3/5 3/10 1/10
巩固练习
1、下列A、B、C、D四个表,其中能成为随机变量X的分布列的是( )
A
X 0 1
P 0.6 0.3
B
X 0 1 2
P 0 0.8 0.2
C
D
B
X 1 2 3
P 0.5 0.4 0.2
X -1 1 2
P 0.5 0.8 -0.3
2.设随机变量ξ的分布列如下:
则a的值为 .
3.设随机变量ξ的分布列:
巩固练习
1、在射击的随机试验中,令X= 如
果射中的概率为0.8,求随机变量X的分布列.
0,射中,
1,未射中
2、设某项试验的成功率是失败率的2倍,用随机变量X去描述1次试验的成功次数,则失败率p等于( )
A.0 B. C. D.
C
巩固练习
X 0 1
P 0.8 0.2
例6.已知随机变量X的分布列如下:
X
-2
-1
3
2
1
0
分别求出随机变量⑴Y1= X
(2)Y2= X2的分布列.
例题讲评
解:
且相应取值的概率没有变化
∴Y1的分布列为:
Y1
P
-1
1
0
⑴由
可得Y1
的取值为
,0,
,1,
例6.已知随机变量X的分布列如下:
X
-2
-1
3
2
1
0
分别求出随机变量⑴Y1= X
(2)Y2= X2的分布列.
解:
∴
Y2的分布列为:
⑵由Y2= X2可得Y2的取值为0、1、4、9
0
9
4
1
例题讲评
一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以X表示取出的3个球中的最小号码,试写出X的分布列.
解: 随机变量X的可取值为 1,2,3.
当X=1时,即取出的三只球中的最小号码为1,则其它两只球只能在编号为2,3,4,5的四只球中任取两只,故有P(X=1)= =3/5;
同理可得 P(X=2)=3/10;P(X=3)=1/10.
因此,X 的分布列如下表所示
X 1 2 3
P 3/5 3/10 1/10
注:在写出X的分布列后,要及时检查所有的概率之和是否为1.
巩固练习
分布列的概念:
课堂小结
上表称为离散型随机变量 的概率分布列,简称为 的分布列.有时为了表达简单,也用等式 ( = )= , =1,2, , 表示 的分布列.
求分布列的步骤:
(1)找出随机变量X的所有可能的取值
(2)求出各取值的概率P(X=xi)=Pi
(3)列成表格。
1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单问题;
3 、两点分布
4 、超几何分布
课堂小结
