7.3.1离散型随机变量的均值2 课件(共22张PPT)
文档属性
| 名称 | 7.3.1离散型随机变量的均值2 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 608.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
7.3.1离散型随机变量的均值2
离散型随机变量的分布列
为随机变量X的概率分布列,简称X的分布列。
我们称X取每一个值 ( =1,2, )的概率 ( = )= ,i=1,2,3 xn
设离散型随机变量X可能取的值为 1, 2, 3, ,
1、概率分布列(分布列)
注意:①.列出随机变量的所有可能取值;
②.求出随机变量的每一个值发生的概率.
求随机变量X的分布列的步骤如下:
(1).确定 X 的可能取值 xi ;
(2).求出相应的概率 P=(X=xi)= pi ;
(3).列成表格的形式.
复习引入
≥
1
概率之和
2、离散型随机变量分布列的性质:
1. 期望的概念E(X)=x1p1+x2p2+…+xipi+…+xnpn
2. 期望的意义离散型随机变量的期望,反映了随机变量取值的平均水平.
3.求离散型随机变量X的期望的基本步骤
(1)理解X的实际意义,写出X全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式求出均值
4.特殊随机变量的均值: 两点分布的期望:E(X)=p.
复习引入
设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) EY=?
思考:
···
···
···
···
学习新知
···
···
···
···
···
···
···
···
···
···
学习新知
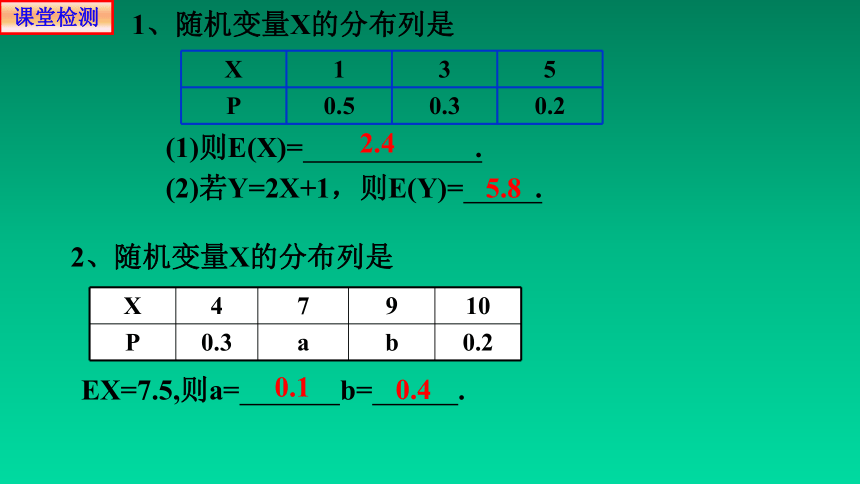
1、随机变量X的分布列是
X 1 3 5
P 0.5 0.3 0.2
(1)则E(X)= .
2、随机变量X的分布列是
2.4
(2)若Y=2X+1,则E(Y)= .
5.8
X 4 7 9 10
P 0.3 a b 0.2
EX=7.5,则a= b= .
0.4
0.1
课堂检测
已知X的概率分布列为
练习提高
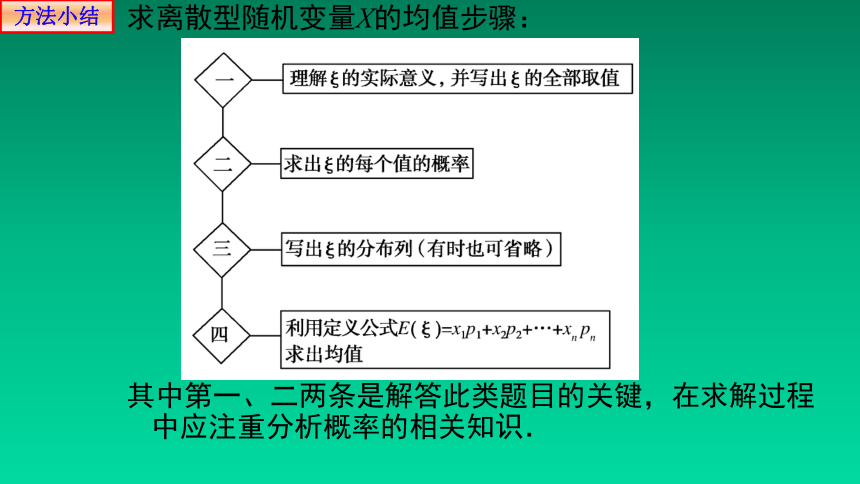
求离散型随机变量X的均值步骤:
其中第一、二两条是解答此类题目的关键,在求解过程中应注重分析概率的相关知识.
方法小结
如图所示,A,B两点之间有6条并联网线,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中取三条网线.
(1)设从A到B可通过的信息总量为x,当x≥6时,可保证使网线通过最大信息量信息畅通,求线路信息畅通的概率;
典型例题
如图所示,A,B两点之间有6条并联网线,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中取三条网线.
(2)求通过的信息总量的数学期望.
练习提高
1.某工厂为检验产品质量,从第一天生产的产品中随机抽取5件作为甲组样品,从第二天生产的产品中随机抽取10件作为乙组样品.经检验两组样品中均有2件次品,其他均为正品.现采用分层抽样从甲、乙两组样品中共抽取3件作为标本进行详细的技术分析.设抽取的标本中次品件数为X,求X的分布列和期望E(X).
练习提高
∴X的分布列为
已知随机变量X的分布列如下:
典型例题
求均值的关键是求出分布列,只要求出了随机变量的分布列,就可以套用均值的公式求解,对于aX+b型随机变量的均值,可以利用E(aX+b)=aE(X)+b求解,当然也可以先求出aX+b的分布列,再用定义求解.
某学校为调查高二年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作用后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高二学生中抽取了50名学生进行问卷调查.问卷调查完成后,学校从学生每天晚自习自主支配学习时间在[20,30)和[30,40)分钟的学生中分别抽取3人和4人,共7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取2名学生聘为学情调查联系人,设[20,30)分钟的学生被聘的人数为X,求X的分布列与数学期望.
练习提高
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果.
指标值分组 [90,94) [94,98) [98,102) [102,106) [106,110]
A配方的频数 8 20 42 22 8
B配方的频数 4 12 42 32 10
练习提高
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
解:(1)由试验结果知,用A配方生产的产品中优质品的频率为=0.3,所以用A配方生产的产品的优质品率的估计值为0.3.
X -2 2 4
P 0.04 0.54 0.42
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
练习提高
X 6 2 1 -2
P 0.63 0.25 0.1 0.02
(2)E(X)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为
E(X)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01
=4.76-x(0≤x≤0.29) 依题意,E(X)≥4.73,即4.76-x≥4.73.
解得x≤0.03,所以三等品率最多为3%.
4.某城市出租汽车的起步价为10元,行驶路不超出4 km时租车费为10元,若行驶路程超出4 km,则按每超出1 km加收2元计费(超出不足1 km的部分按1 km计).从这个城市的民航机场到某宾馆的路程为15 km.某司机经常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按1 km路程计费,不足5分钟的部分不计费),这个司机一次接送旅客的转换后的行车路程X是一个随机变量.设他所收租车费为Y.
练习提高
(1)求租车费Y关于行车路程X的关系式;
(2)若随机变量X的分布列为
求所收租车费Y的数学期望.
(3)已知某旅客实付租车费38元,而出租汽车实际行驶了15 km,问出租车在途中因故停车累计多长时间?
X 15 16 17 18
P 0.1 0.5 0.3 0.1
解析: (1)依题意得Y=2(X-4)+10,
即Y=2X+2,X≥15,X∈N;
(2)E(X)=15×0.1+16×0.5+17×0.3+18×0.1=16.4.
∵Y=2X+2,∴E(Y)=E(2X+2)=2E(X)+2=34.8(元),
故所收租车费Y的数学期望为34.8元.
(3)由38=2X+2,解得X=18,
故停车时间t转换的行车路程为18-15=3 km,∴3×5<t<4×5,
即出租车在途中因故停车累计时间t∈(15,20).
0.03
0.97
P
1000-a
1000
X
E(X)= 1000-0.03a≥0.07a
得a≤10000
故最大定为10000元。
巩固练习
每人交保险费1000元,出险概率为3%,若保险公司的赔偿金为a(a>1000)元,为使保险公司收益的期望值不低于a的百分之七,则保险公司应将最大赔偿金定为多少元?
2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)
0.34
0.33×0.7
0.32×0.7
0.3×0.7
0.7
p
5
4
3
2
1
X
E(X)=1.43
1.离散型随机变量的均值或数学期望
(1)定义:若离散型随机变量X的分布列为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
则称E(X)= 随机变量X的均值或数学期望.
(2)意义:它反映了离散型随机变量取值的 .
(3)性质:如果X为(离散型)随机变量,则Y=aX+b(其中a,b为常数)也是随机变量,且 =P(X=xi),i=1,2,3,…,n.
E(Y)= = .
x1p1+x2p2+…+xnpn
平均水平
P(Y=ax+b)
E(aX+b)
aE(X)+b
课堂小结
如果随机变量X服从两点分布,
X 1 0
P p 1-p
则
7.3.1离散型随机变量的均值2
离散型随机变量的分布列
为随机变量X的概率分布列,简称X的分布列。
我们称X取每一个值 ( =1,2, )的概率 ( = )= ,i=1,2,3 xn
设离散型随机变量X可能取的值为 1, 2, 3, ,
1、概率分布列(分布列)
注意:①.列出随机变量的所有可能取值;
②.求出随机变量的每一个值发生的概率.
求随机变量X的分布列的步骤如下:
(1).确定 X 的可能取值 xi ;
(2).求出相应的概率 P=(X=xi)= pi ;
(3).列成表格的形式.
复习引入
≥
1
概率之和
2、离散型随机变量分布列的性质:
1. 期望的概念E(X)=x1p1+x2p2+…+xipi+…+xnpn
2. 期望的意义离散型随机变量的期望,反映了随机变量取值的平均水平.
3.求离散型随机变量X的期望的基本步骤
(1)理解X的实际意义,写出X全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式求出均值
4.特殊随机变量的均值: 两点分布的期望:E(X)=p.
复习引入
设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) EY=?
思考:
···
···
···
···
学习新知
···
···
···
···
···
···
···
···
···
···
学习新知
1、随机变量X的分布列是
X 1 3 5
P 0.5 0.3 0.2
(1)则E(X)= .
2、随机变量X的分布列是
2.4
(2)若Y=2X+1,则E(Y)= .
5.8
X 4 7 9 10
P 0.3 a b 0.2
EX=7.5,则a= b= .
0.4
0.1
课堂检测
已知X的概率分布列为
练习提高
求离散型随机变量X的均值步骤:
其中第一、二两条是解答此类题目的关键,在求解过程中应注重分析概率的相关知识.
方法小结
如图所示,A,B两点之间有6条并联网线,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中取三条网线.
(1)设从A到B可通过的信息总量为x,当x≥6时,可保证使网线通过最大信息量信息畅通,求线路信息畅通的概率;
典型例题
如图所示,A,B两点之间有6条并联网线,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中取三条网线.
(2)求通过的信息总量的数学期望.
练习提高
1.某工厂为检验产品质量,从第一天生产的产品中随机抽取5件作为甲组样品,从第二天生产的产品中随机抽取10件作为乙组样品.经检验两组样品中均有2件次品,其他均为正品.现采用分层抽样从甲、乙两组样品中共抽取3件作为标本进行详细的技术分析.设抽取的标本中次品件数为X,求X的分布列和期望E(X).
练习提高
∴X的分布列为
已知随机变量X的分布列如下:
典型例题
求均值的关键是求出分布列,只要求出了随机变量的分布列,就可以套用均值的公式求解,对于aX+b型随机变量的均值,可以利用E(aX+b)=aE(X)+b求解,当然也可以先求出aX+b的分布列,再用定义求解.
某学校为调查高二年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作用后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高二学生中抽取了50名学生进行问卷调查.问卷调查完成后,学校从学生每天晚自习自主支配学习时间在[20,30)和[30,40)分钟的学生中分别抽取3人和4人,共7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取2名学生聘为学情调查联系人,设[20,30)分钟的学生被聘的人数为X,求X的分布列与数学期望.
练习提高
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果.
指标值分组 [90,94) [94,98) [98,102) [102,106) [106,110]
A配方的频数 8 20 42 22 8
B配方的频数 4 12 42 32 10
练习提高
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
解:(1)由试验结果知,用A配方生产的产品中优质品的频率为=0.3,所以用A配方生产的产品的优质品率的估计值为0.3.
X -2 2 4
P 0.04 0.54 0.42
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
练习提高
X 6 2 1 -2
P 0.63 0.25 0.1 0.02
(2)E(X)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为
E(X)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01
=4.76-x(0≤x≤0.29) 依题意,E(X)≥4.73,即4.76-x≥4.73.
解得x≤0.03,所以三等品率最多为3%.
4.某城市出租汽车的起步价为10元,行驶路不超出4 km时租车费为10元,若行驶路程超出4 km,则按每超出1 km加收2元计费(超出不足1 km的部分按1 km计).从这个城市的民航机场到某宾馆的路程为15 km.某司机经常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按1 km路程计费,不足5分钟的部分不计费),这个司机一次接送旅客的转换后的行车路程X是一个随机变量.设他所收租车费为Y.
练习提高
(1)求租车费Y关于行车路程X的关系式;
(2)若随机变量X的分布列为
求所收租车费Y的数学期望.
(3)已知某旅客实付租车费38元,而出租汽车实际行驶了15 km,问出租车在途中因故停车累计多长时间?
X 15 16 17 18
P 0.1 0.5 0.3 0.1
解析: (1)依题意得Y=2(X-4)+10,
即Y=2X+2,X≥15,X∈N;
(2)E(X)=15×0.1+16×0.5+17×0.3+18×0.1=16.4.
∵Y=2X+2,∴E(Y)=E(2X+2)=2E(X)+2=34.8(元),
故所收租车费Y的数学期望为34.8元.
(3)由38=2X+2,解得X=18,
故停车时间t转换的行车路程为18-15=3 km,∴3×5<t<4×5,
即出租车在途中因故停车累计时间t∈(15,20).
0.03
0.97
P
1000-a
1000
X
E(X)= 1000-0.03a≥0.07a
得a≤10000
故最大定为10000元。
巩固练习
每人交保险费1000元,出险概率为3%,若保险公司的赔偿金为a(a>1000)元,为使保险公司收益的期望值不低于a的百分之七,则保险公司应将最大赔偿金定为多少元?
2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)
0.34
0.33×0.7
0.32×0.7
0.3×0.7
0.7
p
5
4
3
2
1
X
E(X)=1.43
1.离散型随机变量的均值或数学期望
(1)定义:若离散型随机变量X的分布列为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
则称E(X)= 随机变量X的均值或数学期望.
(2)意义:它反映了离散型随机变量取值的 .
(3)性质:如果X为(离散型)随机变量,则Y=aX+b(其中a,b为常数)也是随机变量,且 =P(X=xi),i=1,2,3,…,n.
E(Y)= = .
x1p1+x2p2+…+xnpn
平均水平
P(Y=ax+b)
E(aX+b)
aE(X)+b
课堂小结
如果随机变量X服从两点分布,
X 1 0
P p 1-p
则
