7.5正态分布 课件(共26张PPT)
文档属性
| 名称 | 7.5正态分布 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 21:25:07 | ||
图片预览








文档简介
(共26张PPT)
7.5 正态分布
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文明影响最大的是正态分布.
那么,什么是正态分布?正态分布的曲线有什么特征?
新课引入
正态分布在统计学中是很重要的分布。我们知道,离散型随机变量最多取可列个不同值,它等于某一特定实数的概率可能大于0,人们感兴趣的是它取某些特定值的概率,即感兴趣的是其分布列;连续型随机变量可能取某个区间上的任何值,它等于任何一个实数的概率都为0,所以通常感兴趣的是它落在某个区间的概率。我们称这类随机变量为连续型随机变量(continuous random variable).离散型随机变量的概率分布规律用分布列描述,而连续型随机变量的概率分布规律用密度函数(曲线)描述。
新课引入
问题:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控的因素,任意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员在一次产品检验中, 随机抽取了100袋食盐,获得误差X (单位:g)的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1).如何描述这100个样本误差数据的分布
(2).如何构建适当的概率模型刻画误差X的分布
新课引入
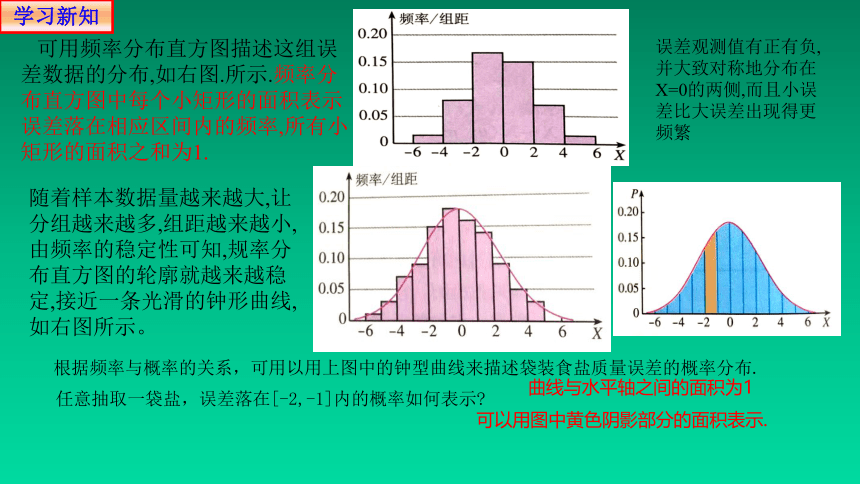
可用频率分布直方图描述这组误差数据的分布,如右图.所示.频率分布直方图中每个小矩形的面积表示误差落在相应区间内的频率,所有小矩形的面积之和为1.
根据频率与概率的关系,可用以用上图中的钟型曲线来描述袋装食盐质量误差的概率分布.
曲线与水平轴之间的面积为1
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示
可以用图中黄色阴影部分的面积表示.
学习新知
误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,规率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如右图所示。
2.正态密度曲线(简称正态曲线)
0
Y
X
相应的函数解析式为:
称为正态密度函数
学习新知
正态分布的定义
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
学习新知
对任意的x∈R,f(x)>0,它的图象在x轴的上方.
可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如上图所示.
若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal dis-tribution),记为X~N(u,σ2).特别地,当u=0, σ=1时,称随机变量X服从标准正态分布.
若X~N(u,σ2),则如上图所示,
X取值不超过x的概率P(X)为图中区域A的面积,
而P(a≤X正态分布在概率和统计中占有重要地位,它广泛存在于自然现象、生产和生活实践之中.在现实生活中,很多随机变量都服从或近似服从正态分布
例如,某些物理量的测量误差某一地区同年龄人群的身高、体重、肺活量等一定条件下生长的小麦的株高、穗长、单位面积产量自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容)某地每年7月的平均气温、平均湿度、降水量等
一般都近似服从正态分布
右图所示的就是一块高尔顿板示意图.在一块木板上钉上若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃让一个
高尔顿板
小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内
如果把球槽编号,就可以考察到底是落在第几号球槽中.重复进行高尔顿板试验,随着试验次数的增加,掉入各个球槽内的小球的个数就 越来越多 ,堆积的高度也会越来越高 .各个球槽的堆积高度反映了小球掉入各球槽的个数多少
例1、下列函数是正态密度函数的是( )
A.
B.
C. D.
B
典型例题
正态密度的函数表示式
具有两头低、中间高、左右对称的基本特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
思考:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
正态曲线的性质
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
x=m
x=m
x=m
(3)当 无限增大时,曲线无限接近 轴.
当x∈(-∞,μ]时,为增函数.
当x∈[μ,+∞)时,为减函数.
值域为
正态曲线的性质
参数 含义及对正态曲线的形状的影响
一个正态分布由参数 和 完全确定,这两个参数对
正态曲线的形状有何影响 它们反映正态分布的哪些特征
学习新知
3
1
2
σ=1
μ= -1
μ=0
μ=1
若 固定, 随 值的 变化而沿x轴平移, 故 称为位置参数;
x
y
(1).当参数 取定值时
=0.5
=1
=2
μ=0
若 固定,
大时, 曲线“矮而胖”;
小时, 曲线“瘦而高”,
故称 为形状参数.
所以σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
x
y
(2).当参数 取定值时
例:李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布。
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38min可用,李明应选择哪种交通工具 如果某天只有34min可用,又应该选择哪种交通工具 请说明理由。
分析:对于第(1)问,正态分布由参数μ和σ 完全确定,根据正态分布参数的意义可以分别用样本均值和样本标准差来估计.
对于第(3)问,这是一个概率决策问题,首先要明确决策的准则,在给定的时间内选择不迟到概率大的交通工具;然后结合图形,相据概率的表示,比较概率的大小,作出判断
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ.用样本标准差估计参数σ,可以得到X~N(30,6),Y~N(34,2).
(2)X和Y的分布密度曲线如图所示,
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图可知,Y的密度曲线X的密度曲线P(X≤38)P(Y ≤ 34).
所以,如果有38min可用,那么骑自行车不迟到的概率大,应选择骑自行车;
如果只有34min可用,那么坐公交车不迟到的概率大,应选择坐公交车,
26
30
34
38
t
y
典型例题
正态分布的3σ原则
学习新知
尽管正态变量的取值范围是( ∞,+∞),但在一次试验中, 的取值几乎总落在区间[ 3 , +3 ]内,而在此区间外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布 ( , 2)的随机变量 只取[ 3 , +3 ]中的值,这在统计学中称为3 原则.
例3.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人
解:(1)依题意,X~N(90,100),
即考试成绩在(80,100)间的概率为0.6827.
考试成绩在(80,100)间的考生大约有
例4.若X~N(5,1),求P(6解:因为X~N(5,1),
故正态密度曲线关于直线 x=5 对称,
例2、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
D
典型例题
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
巩固练习
2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9545 B.0.0456 C.0.9772 D.0.02275
3、设离散型随机变量X~N(0,1),则 = ,
= .
D
0.5
0.9545
1、已知一次考试共有60名同学参加,考生的成绩X~N(100,52) ,据此估计,大约应有57人的分数在下列哪个区间内?( )
(90,110] B. (95,125] C. (100,120] D.(105,115]
A
巩固练习
课堂小结
1.正态曲线及正态密度函数
2.正态分布
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
3、正态曲线的性质
(4)曲线与x轴之间的面积为1
(3)曲线在x=μ处达到峰值(最高点)
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越矮胖,表示总体的分布越分散;
σ越小,曲线越瘦高,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
4.正态分布的 原则
7.5 正态分布
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文明影响最大的是正态分布.
那么,什么是正态分布?正态分布的曲线有什么特征?
新课引入
正态分布在统计学中是很重要的分布。我们知道,离散型随机变量最多取可列个不同值,它等于某一特定实数的概率可能大于0,人们感兴趣的是它取某些特定值的概率,即感兴趣的是其分布列;连续型随机变量可能取某个区间上的任何值,它等于任何一个实数的概率都为0,所以通常感兴趣的是它落在某个区间的概率。我们称这类随机变量为连续型随机变量(continuous random variable).离散型随机变量的概率分布规律用分布列描述,而连续型随机变量的概率分布规律用密度函数(曲线)描述。
新课引入
问题:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控的因素,任意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员在一次产品检验中, 随机抽取了100袋食盐,获得误差X (单位:g)的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1).如何描述这100个样本误差数据的分布
(2).如何构建适当的概率模型刻画误差X的分布
新课引入
可用频率分布直方图描述这组误差数据的分布,如右图.所示.频率分布直方图中每个小矩形的面积表示误差落在相应区间内的频率,所有小矩形的面积之和为1.
根据频率与概率的关系,可用以用上图中的钟型曲线来描述袋装食盐质量误差的概率分布.
曲线与水平轴之间的面积为1
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示
可以用图中黄色阴影部分的面积表示.
学习新知
误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,规率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如右图所示。
2.正态密度曲线(简称正态曲线)
0
Y
X
相应的函数解析式为:
称为正态密度函数
学习新知
正态分布的定义
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
学习新知
对任意的x∈R,f(x)>0,它的图象在x轴的上方.
可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如上图所示.
若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal dis-tribution),记为X~N(u,σ2).特别地,当u=0, σ=1时,称随机变量X服从标准正态分布.
若X~N(u,σ2),则如上图所示,
X取值不超过x的概率P(X)为图中区域A的面积,
而P(a≤X
例如,某些物理量的测量误差某一地区同年龄人群的身高、体重、肺活量等一定条件下生长的小麦的株高、穗长、单位面积产量自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容)某地每年7月的平均气温、平均湿度、降水量等
一般都近似服从正态分布
右图所示的就是一块高尔顿板示意图.在一块木板上钉上若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃让一个
高尔顿板
小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内
如果把球槽编号,就可以考察到底是落在第几号球槽中.重复进行高尔顿板试验,随着试验次数的增加,掉入各个球槽内的小球的个数就 越来越多 ,堆积的高度也会越来越高 .各个球槽的堆积高度反映了小球掉入各球槽的个数多少
例1、下列函数是正态密度函数的是( )
A.
B.
C. D.
B
典型例题
正态密度的函数表示式
具有两头低、中间高、左右对称的基本特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
思考:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
正态曲线的性质
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
x=m
x=m
x=m
(3)当 无限增大时,曲线无限接近 轴.
当x∈(-∞,μ]时,为增函数.
当x∈[μ,+∞)时,为减函数.
值域为
正态曲线的性质
参数 含义及对正态曲线的形状的影响
一个正态分布由参数 和 完全确定,这两个参数对
正态曲线的形状有何影响 它们反映正态分布的哪些特征
学习新知
3
1
2
σ=1
μ= -1
μ=0
μ=1
若 固定, 随 值的 变化而沿x轴平移, 故 称为位置参数;
x
y
(1).当参数 取定值时
=0.5
=1
=2
μ=0
若 固定,
大时, 曲线“矮而胖”;
小时, 曲线“瘦而高”,
故称 为形状参数.
所以σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
x
y
(2).当参数 取定值时
例:李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布。
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38min可用,李明应选择哪种交通工具 如果某天只有34min可用,又应该选择哪种交通工具 请说明理由。
分析:对于第(1)问,正态分布由参数μ和σ 完全确定,根据正态分布参数的意义可以分别用样本均值和样本标准差来估计.
对于第(3)问,这是一个概率决策问题,首先要明确决策的准则,在给定的时间内选择不迟到概率大的交通工具;然后结合图形,相据概率的表示,比较概率的大小,作出判断
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ.用样本标准差估计参数σ,可以得到X~N(30,6),Y~N(34,2).
(2)X和Y的分布密度曲线如图所示,
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图可知,Y的密度曲线X的密度曲线P(X≤38)
所以,如果有38min可用,那么骑自行车不迟到的概率大,应选择骑自行车;
如果只有34min可用,那么坐公交车不迟到的概率大,应选择坐公交车,
26
30
34
38
t
y
典型例题
正态分布的3σ原则
学习新知
尽管正态变量的取值范围是( ∞,+∞),但在一次试验中, 的取值几乎总落在区间[ 3 , +3 ]内,而在此区间外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布 ( , 2)的随机变量 只取[ 3 , +3 ]中的值,这在统计学中称为3 原则.
例3.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人
解:(1)依题意,X~N(90,100),
即考试成绩在(80,100)间的概率为0.6827.
考试成绩在(80,100)间的考生大约有
例4.若X~N(5,1),求P(6
故正态密度曲线关于直线 x=5 对称,
例2、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
D
典型例题
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
巩固练习
2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9545 B.0.0456 C.0.9772 D.0.02275
3、设离散型随机变量X~N(0,1),则 = ,
= .
D
0.5
0.9545
1、已知一次考试共有60名同学参加,考生的成绩X~N(100,52) ,据此估计,大约应有57人的分数在下列哪个区间内?( )
(90,110] B. (95,125] C. (100,120] D.(105,115]
A
巩固练习
课堂小结
1.正态曲线及正态密度函数
2.正态分布
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
3、正态曲线的性质
(4)曲线与x轴之间的面积为1
(3)曲线在x=μ处达到峰值(最高点)
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越矮胖,表示总体的分布越分散;
σ越小,曲线越瘦高,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
4.正态分布的 原则
