8.3.2独立性检验 课件(共30张PPT)
文档属性
| 名称 | 8.3.2独立性检验 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-02 22:50:53 | ||
图片预览









文档简介
(共30张PPT)
8.3列联表与独立性检验
8.3.2 独立性检验
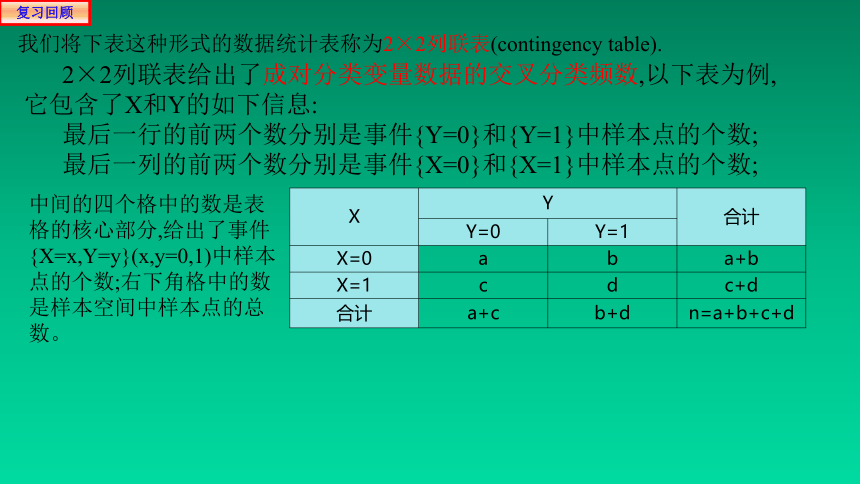
我们将下表这种形式的数据统计表称为2×2列联表(contingency table).
复习回顾
2×2列联表给出了成对分类变量数据的交叉分类频数,以下表为例,它包含了X和Y的如下信息:
最后一行的前两个数分别是事件{Y=0}和{Y=1}中样本点的个数;
最后一列的前两个数分别是事件{X=0}和{X=1}中样本点的个数;
中间的四个格中的数是表格的核心部分,给出了事件{X=x,Y=y}(x,y=0,1)中样本点的个数;右下角格中的数是样本空间中样本点的总数。
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
复习回顾
两个分类变量之间关联关系的定性分析的方法:
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
如可以通过列联表中值的大小粗略地判断分类变量x和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
考虑以Ω为样本空间的古典概型,设X和Y为定义在Ω上,取值于{0,1}的成对分类变量,我们希望判断事件{X=1}和{Y=1}之间是否有关联。注意到{X=0}和{X=1}, {Y=0}和{Y=1}都是互对立事件,与前面的讨论类似,我们需要判断下面的假定关系H0:P(Y=1|X=0)=P(Y=1|X=1)是否成立,通常称H0为零假设或原假设(null hypothesis).
P(Y=1|X=0)表示从{X=0}中随机选取一个样本点,该样本点属于{X=0,Y=1}的概率;
P(Y=1|X=1)表示从{X=1}中随机选取一个样本点,该样本点属于{X=1,Y=1}的概率。由条件概率的定义可知,零假设H0等价于=
或P(X=0,Y=1)P(X=1)=P(X=1,Y=1)P(X=0). ①
考虑以Ω为样本空间的古典概型,设X和Y为定义在Ω上,取值于{0,1}的成对分类变量,我们希望判断事件{X=1}和{Y=1}之间是否有关联。注意到{X=0}和{X=1}, {Y=0}和{Y=1}都是互对立事件,与前面的讨论类似,我们需要判断下面的假定关系H0:P(Y=1|X=0)=P(Y=1|X=1)是否成立,通常称H0为零假设或原假设(null hypothesis).
P(Y=1|X=0)表示从{X=0}中随机选取一个样本点,该样本点属于{X=0,Y=1}的概率;
P(Y=1|X=1)表示从{X=1}中随机选取一个样本点,该样本点属于{X=1,Y=1}的概率。由条件概率的定义可知,零假设H0等价于=
或P(X=0,Y=1)P(X=1)=P(X=1,Y=1)P(X=0). ①
注意到(X=0)和(X=1)为对立事件,于是P(X=0)=1-P(X=1).
再由概率的性质,我们有P(X=0,Y=1)=P(Y=1)-P(X=1,Y=1).
由此推得①式等价于P(X=1)P(Y=1)=P(X=1,Y=1).
因此,零假设H0等价于{X=1}与{Y=1}独立。
根据已经学过的概率知识,下面的四条性质彼此等价:
{X=0}与{Y=0}独立;{X=0}与{Y=1}独立;{X=1}与{Y=0}独立;{X=1}与{Y=1}独立。
学习新知
以上性质成立,我们就称分类变量X和Y独立,这相当于下面四个等式成立;
P(X=0,Y=0)=P(X=0)P(Y=0); P(X=0,Y=1)=P(X=0)P(Y=1);
P(X=1,Y=0)=P(X=1)P(Y=0); P(X=1,Y=1)=P(X=1)P(Y=1).
我们可以用概率语言,将零假设改述为H0:分类变量X和Y独立.
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,如下表所示。
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
对于随机样本,表中的频数a,b,c,d 都是随机变量,而表中的相应数据是这些随机变量的一次观测结果。
表是关于分类变量X和Y的抽样数据的2×2列联表:
最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;
最后一列的前两个数分别是事件{X=0}和{X=1}的频数;
中间的四个数a,b,c,d是事件{X=x,Y=y}(x, y=0,1)的频数;
右下角格中的数n是样本容量。
②
思考:如何基于②中的四个等式及列联表中的数据,构造适当的统计量,对成对分类变量X和Y是否相互独立作出推断
P(X=0,Y=0)=P(X=0)P(Y=0); P(X=0,Y=1)=P(X=0)P(Y=1);
P(X=1,Y=0)=P(X=1)P(Y=0); P(X=1,Y=1)=P(X=1)P(Y=1).
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
在零假设H0成立的条件下,根据频率稳定于概率的原理,由②中的第一个等式,我们可以用概率P(X=0)和P(Y=0)对应的频率的乘积估计概率P(X=0,Y=0),而把视为事件{X=0.Y=0}发生的频数的期望值(或预期值).
这样,该频数的观测值a和期望值应该比较接近.
综合②中的四个式子,如果零假设H0成立,下面四个量的取值都不应该太大:
|, |, |, | ③
反之,当这些量的取值较大时,就可以推断H0不成立。
分别考虑③中的四个差的绝对值很困难,我们需要找到一个既合理又能够计算分布的统计量,来推断H0是否成立.
一般来说,若频数的期望值较大,则③中相应的差的绝对值也会较大;
而若频数的期望值较小,则③中相应的差的绝对值也会较小.
为了合理地平衡这种影响,我们将四个差的绝对值取平方后分别除以相应的期望值再求和,得到如下的统计量:
该表达式可化简为
.
统计学家建议,用随机变量取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立.
那么,究竟大到什么程度,可以推断H0不成立呢 或者说,怎样确定判断大小的标准呢
根据小概率事件在一次试验中不大可能发生的规律, 可以通过确定一个与H0相矛盾的小概率事件来实现,在假定H0的条件下,对于有放回简单随机抽样,当样本容量n充分大时,统计学家得到了的近似分布,忽略的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得下面关系成立:P(≥xα)=α ④
我们称xα为α的临界值,这个临界值就可作为判断大小的标准,概率值α越小,临界值xα越大,当总体很大时,抽样有、无放回对的分布影响较小.因此,在应用中往往不严格要求抽样必须是有放回的.
由④式可知,只要把概率值α取得充分小,在假设H0成立的情况下,事件不大可能发生的.根据这个规律,如果该事件发生,我们就可以推断H0不成立.不过这个推断有可能犯错误,但犯错误的概率不会超过α.
独立性检验公式及定义:
提出零假设(原假设)H0:分类变量X和Y独立
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,在列联表中,如果零假设H0成立,则应满足,即ad-bc≈0.因此|ad bc|越小,说明两个分类变量之间关系越弱;|ad bc|越大,说明两个分类变量之间关系越强.
2 =
χ
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
学习新知
χ2独立性检验中几个常用的小概率值和相应的临界值.
10.828
7.879
6.635
3.841
2.706
xα
0.001
0.005
0.01
0.05
0.1
α
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
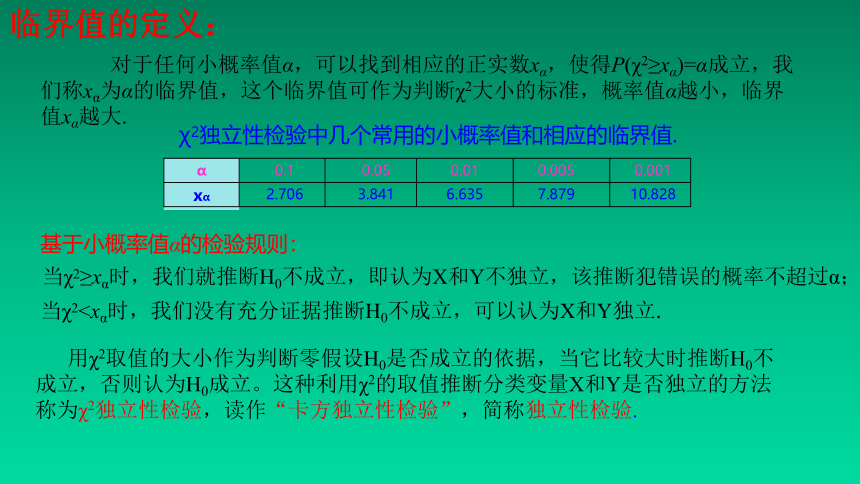
临界值的定义:
对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2≥xα)=α成立,我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
χ2独立性检验中几个常用的小概率值和相应的临界值.
基于小概率值α的检验规则:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ210.828
7.879
6.635
3.841
2.706
xα
0.001
0.005
0.01
0.05
0.1
α
用χ2取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立。这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
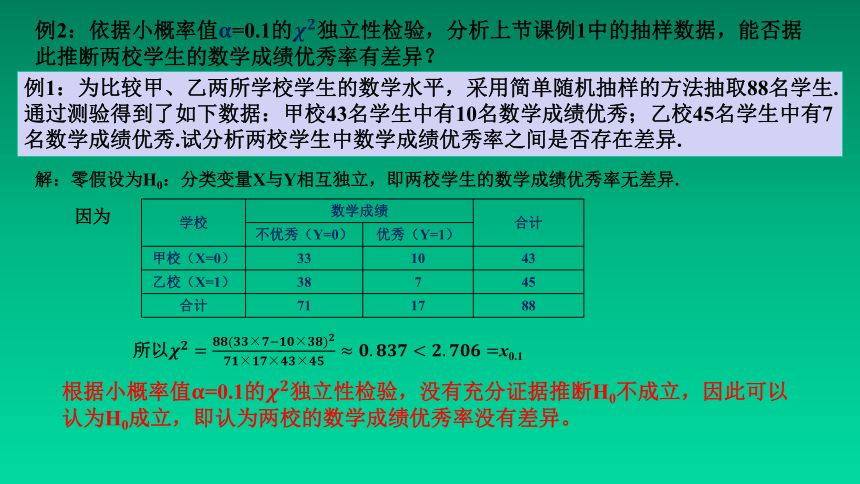
例2:依据小概率值=0.1的独立性检验,分析上节课例1中的抽样数据,能否据此推断两校学生的数学成绩优秀率有差异?
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:零假设为H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异.
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
因为
所以x0.1
根据小概率值=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为两校的数学成绩优秀率没有差异。
思考例1和例2都是基于同一组数据的分析,但却得出了不同的结论,你能说明其中的原因吗
例1只是根据一个样本的两个频率间存在差异得出两校学生数学成绩优秀率有差异的结论,并没有考虑由样本随机性可能导致的错误,所以那里的推断依据不太充分,在本例中,我们用独立性检验对零假设H0进行了检验,通过计算,发现≈0.837小于α=0.1所对应的临界值2.706,因此认为没有充分证据推断H0不成立,所以接受H0,推断出两校学生的数学优秀率没有显著差异的结论,
这个检验结果意味着,抽样数据中两个频率的差异很有可能是由样本随机性导致的,因此,只根据频率的差异得出两校学生的数学成绩优秀率有差异的结论是不可靠的。
由此可见,相对于简单比较两个频率的推断,用独立性检验得到的结果更理性、更全面,理论依据也更充分。
当我们接受零假设H0时,也可能犯错误。我们不知道犯这类错误的概率p的大小,但是知道,若α越大,则p越小
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
根据列联表中的数据,经计算得到
根据小概率值=0.005的独立性检验,没有充分证据推断 H0不成立,因此可以认为 H0成立,即认为两种疗法效果没有差异.
追问1:若对调两种疗法的位置或对调两种疗效的位置,这样做会影响取值的计算结果吗?
不影响
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
疗法 疗效 合计
未治愈 治愈 乙 6 63 69
甲 15 52 67
合计 21 115 136
疗法 疗效 合计
治愈 未治愈 甲 52 15 67
乙 63 6 69
合计 115 21 136
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
追问2:根据小概率值=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
根据小概率值=0.05的独立性检验,我们推断 H0不成立,即可以认为两种疗法效果有差异,该推断犯错误的概率不超过0.05.
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
根据列联表中的数据,经计算得到
追问2:根据小概率值=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:
甲种疗法未治愈和治愈的频率分别是和
乙种疗法未治愈和治愈的频率分别是和0.913.
因此可以推断乙种疗法的效果比甲种疗法好。
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
例4:为了调查吸烟是否对肺癌有影响,某肿瘤研究所采取有放回简单随机抽样,调查了9965人,得到如下结果(单位:人)依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险。
解:零假设为H0:吸烟和患肺癌之间没有关系根据列联表中的数据,经计算的
χ2 =
>
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为吸 烟与患肺癌有关联,此推断犯错误的概率不大于0.001,即我们有99.9%的把握认为“吸烟与患肺癌有关系”.
吸烟 肺癌 合计
非肺癌患者 肺癌患者 非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
根据表中的数据计算不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的评率分别为
由
可见,在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌频率的4倍以上。于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌概率,即吸烟更容易引发肺癌。
方法总结
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
应用独立性检验解决实际问题大致应包括以下几个主要环节:
注意:上述几个环节的内容可以根据不同情况进行调整,
例如,在有些时候,分类变量的抽样数据列联表是问题中给定的.
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
0.1%把握认
为A与B无关
1%把握认为A与B无关
99.9%把握认
为A与B有关
99%把握认
为A与B有关
90%把握认
为A与B有关
10%把握认为
A与B无关
没有充分的依据显示A与B有关,但也不能显示A与B无关
例如
学习新知
在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示。问:该种血清能否起到预防感冒的作用?
未感冒 感冒 合计
使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1000
解:设H0:感冒与是否使用该血清没有关系。
因当H0成立时, χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用。
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
典型例题
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
有效 无效 合计
口服 58 40 98
注射 64 31 95
合计 122 71 193
解:设H0:药的效果与给药方式没有关系。
因当H0成立时, 2≥1.3896的概率大于15%,故不能否定假设H0,即不能作出药的效果与给药方式有关的结论。
<2.072
为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查的结果列在表中,根据所选择的193个病人的数据,能否作出药的效果和给药方式有关的结论?
典型例题
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
气管炎是一种常见的呼吸道疾病,医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比,所得数据如表所示,问:它们的疗效有无差异?
有效 无效 合计
复方江剪刀草 184 61 245
胆黄片 91 9 100
合计 275 70 345
解:设H0:两种中草药的治疗效果没有差异。
因当H0成立时, 2≥10.828的概率为0.001,故有99.9%的把握认为,两种药物的疗效有差异。
典型例题
某校对学生的课外活动进行调查,结果整理成下表:
体育 文娱 总计
男生 21 23 44
女生 6 29 35
总计 27 52 79
试用你所学过的知识分析:能否在犯错误的概率不超过0.005的前提下,认为“喜欢体育还是文娱与性别有关系”?
巩固练习
∵a=21,b=23,c=6,d=29,n=79,
即我们得到的K2的观测值k≈8.106超过7.879这就意味着:“喜欢体育还是文娱与性别没有关系”这一结论成立的可能性小于0.005,即在犯错误的概率不超过0.005的前提下认为“喜欢体育还是喜欢文娱与性别有关.”
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
巩固练习
某县城区常见在合法的广告牌上又贴有违法的黑广告,城管对此进行了清理,并下了通告.一周后,城管对某街道进行了检查.作了如下统计:
贴有黑广告 未贴有黑广告 总计
通告前 39 157 196
通告后 29 167 196
总计 68 324 392
请你判断,城管下通告对减少黑广告数是否有效?
巩固练习
巩固练习
C
先假设两个分类变量X与Y无关系,利用上述公式根据观测数据求出K2的观测值k,再得出X与Y有关系的程度.
(1)如果k≥10.828,就有______的把握认为“X与Y有关系” (2)如果k≥7.879,就有______的把握认为“X与Y有关系”;
99.9%
99.5%
(3)如果k≥_____,就有99%的把握认为“X与Y有关系” (4)如果k≥5.024,就有97.5%的把握认为“X与Y有关系” (5)如果k≥3.841,就有_____的把握认为“X与Y有关系” (6)如果k≥2.706,就有_____的把握认为“X与Y有关系”.
6.635
95%
90%
课堂小结
不渴望能够一跃千里,只希望每天能够前进一步。
1.分类变量X和Y的抽样数据的2×2列联表:
课堂小结
2.独立性检验的一般步骤:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释. (2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较. (3)根据检验规则得出推断结论. (4)在X和Y不独立的情况下,根据需要,通过比较相应的频率, 分析X和Y间的影响规律.
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
8.3列联表与独立性检验
8.3.2 独立性检验
我们将下表这种形式的数据统计表称为2×2列联表(contingency table).
复习回顾
2×2列联表给出了成对分类变量数据的交叉分类频数,以下表为例,它包含了X和Y的如下信息:
最后一行的前两个数分别是事件{Y=0}和{Y=1}中样本点的个数;
最后一列的前两个数分别是事件{X=0}和{X=1}中样本点的个数;
中间的四个格中的数是表格的核心部分,给出了事件{X=x,Y=y}(x,y=0,1)中样本点的个数;右下角格中的数是样本空间中样本点的总数。
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
复习回顾
两个分类变量之间关联关系的定性分析的方法:
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
如可以通过列联表中值的大小粗略地判断分类变量x和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
考虑以Ω为样本空间的古典概型,设X和Y为定义在Ω上,取值于{0,1}的成对分类变量,我们希望判断事件{X=1}和{Y=1}之间是否有关联。注意到{X=0}和{X=1}, {Y=0}和{Y=1}都是互对立事件,与前面的讨论类似,我们需要判断下面的假定关系H0:P(Y=1|X=0)=P(Y=1|X=1)是否成立,通常称H0为零假设或原假设(null hypothesis).
P(Y=1|X=0)表示从{X=0}中随机选取一个样本点,该样本点属于{X=0,Y=1}的概率;
P(Y=1|X=1)表示从{X=1}中随机选取一个样本点,该样本点属于{X=1,Y=1}的概率。由条件概率的定义可知,零假设H0等价于=
或P(X=0,Y=1)P(X=1)=P(X=1,Y=1)P(X=0). ①
考虑以Ω为样本空间的古典概型,设X和Y为定义在Ω上,取值于{0,1}的成对分类变量,我们希望判断事件{X=1}和{Y=1}之间是否有关联。注意到{X=0}和{X=1}, {Y=0}和{Y=1}都是互对立事件,与前面的讨论类似,我们需要判断下面的假定关系H0:P(Y=1|X=0)=P(Y=1|X=1)是否成立,通常称H0为零假设或原假设(null hypothesis).
P(Y=1|X=0)表示从{X=0}中随机选取一个样本点,该样本点属于{X=0,Y=1}的概率;
P(Y=1|X=1)表示从{X=1}中随机选取一个样本点,该样本点属于{X=1,Y=1}的概率。由条件概率的定义可知,零假设H0等价于=
或P(X=0,Y=1)P(X=1)=P(X=1,Y=1)P(X=0). ①
注意到(X=0)和(X=1)为对立事件,于是P(X=0)=1-P(X=1).
再由概率的性质,我们有P(X=0,Y=1)=P(Y=1)-P(X=1,Y=1).
由此推得①式等价于P(X=1)P(Y=1)=P(X=1,Y=1).
因此,零假设H0等价于{X=1}与{Y=1}独立。
根据已经学过的概率知识,下面的四条性质彼此等价:
{X=0}与{Y=0}独立;{X=0}与{Y=1}独立;{X=1}与{Y=0}独立;{X=1}与{Y=1}独立。
学习新知
以上性质成立,我们就称分类变量X和Y独立,这相当于下面四个等式成立;
P(X=0,Y=0)=P(X=0)P(Y=0); P(X=0,Y=1)=P(X=0)P(Y=1);
P(X=1,Y=0)=P(X=1)P(Y=0); P(X=1,Y=1)=P(X=1)P(Y=1).
我们可以用概率语言,将零假设改述为H0:分类变量X和Y独立.
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,如下表所示。
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
对于随机样本,表中的频数a,b,c,d 都是随机变量,而表中的相应数据是这些随机变量的一次观测结果。
表是关于分类变量X和Y的抽样数据的2×2列联表:
最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;
最后一列的前两个数分别是事件{X=0}和{X=1}的频数;
中间的四个数a,b,c,d是事件{X=x,Y=y}(x, y=0,1)的频数;
右下角格中的数n是样本容量。
②
思考:如何基于②中的四个等式及列联表中的数据,构造适当的统计量,对成对分类变量X和Y是否相互独立作出推断
P(X=0,Y=0)=P(X=0)P(Y=0); P(X=0,Y=1)=P(X=0)P(Y=1);
P(X=1,Y=0)=P(X=1)P(Y=0); P(X=1,Y=1)=P(X=1)P(Y=1).
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
在零假设H0成立的条件下,根据频率稳定于概率的原理,由②中的第一个等式,我们可以用概率P(X=0)和P(Y=0)对应的频率的乘积估计概率P(X=0,Y=0),而把视为事件{X=0.Y=0}发生的频数的期望值(或预期值).
这样,该频数的观测值a和期望值应该比较接近.
综合②中的四个式子,如果零假设H0成立,下面四个量的取值都不应该太大:
|, |, |, | ③
反之,当这些量的取值较大时,就可以推断H0不成立。
分别考虑③中的四个差的绝对值很困难,我们需要找到一个既合理又能够计算分布的统计量,来推断H0是否成立.
一般来说,若频数的期望值较大,则③中相应的差的绝对值也会较大;
而若频数的期望值较小,则③中相应的差的绝对值也会较小.
为了合理地平衡这种影响,我们将四个差的绝对值取平方后分别除以相应的期望值再求和,得到如下的统计量:
该表达式可化简为
.
统计学家建议,用随机变量取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立.
那么,究竟大到什么程度,可以推断H0不成立呢 或者说,怎样确定判断大小的标准呢
根据小概率事件在一次试验中不大可能发生的规律, 可以通过确定一个与H0相矛盾的小概率事件来实现,在假定H0的条件下,对于有放回简单随机抽样,当样本容量n充分大时,统计学家得到了的近似分布,忽略的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得下面关系成立:P(≥xα)=α ④
我们称xα为α的临界值,这个临界值就可作为判断大小的标准,概率值α越小,临界值xα越大,当总体很大时,抽样有、无放回对的分布影响较小.因此,在应用中往往不严格要求抽样必须是有放回的.
由④式可知,只要把概率值α取得充分小,在假设H0成立的情况下,事件不大可能发生的.根据这个规律,如果该事件发生,我们就可以推断H0不成立.不过这个推断有可能犯错误,但犯错误的概率不会超过α.
独立性检验公式及定义:
提出零假设(原假设)H0:分类变量X和Y独立
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,在列联表中,如果零假设H0成立,则应满足,即ad-bc≈0.因此|ad bc|越小,说明两个分类变量之间关系越弱;|ad bc|越大,说明两个分类变量之间关系越强.
2 =
χ
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
学习新知
χ2独立性检验中几个常用的小概率值和相应的临界值.
10.828
7.879
6.635
3.841
2.706
xα
0.001
0.005
0.01
0.05
0.1
α
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
临界值的定义:
对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2≥xα)=α成立,我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
χ2独立性检验中几个常用的小概率值和相应的临界值.
基于小概率值α的检验规则:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2
7.879
6.635
3.841
2.706
xα
0.001
0.005
0.01
0.05
0.1
α
用χ2取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立。这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
例2:依据小概率值=0.1的独立性检验,分析上节课例1中的抽样数据,能否据此推断两校学生的数学成绩优秀率有差异?
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:零假设为H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异.
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
因为
所以x0.1
根据小概率值=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为两校的数学成绩优秀率没有差异。
思考例1和例2都是基于同一组数据的分析,但却得出了不同的结论,你能说明其中的原因吗
例1只是根据一个样本的两个频率间存在差异得出两校学生数学成绩优秀率有差异的结论,并没有考虑由样本随机性可能导致的错误,所以那里的推断依据不太充分,在本例中,我们用独立性检验对零假设H0进行了检验,通过计算,发现≈0.837小于α=0.1所对应的临界值2.706,因此认为没有充分证据推断H0不成立,所以接受H0,推断出两校学生的数学优秀率没有显著差异的结论,
这个检验结果意味着,抽样数据中两个频率的差异很有可能是由样本随机性导致的,因此,只根据频率的差异得出两校学生的数学成绩优秀率有差异的结论是不可靠的。
由此可见,相对于简单比较两个频率的推断,用独立性检验得到的结果更理性、更全面,理论依据也更充分。
当我们接受零假设H0时,也可能犯错误。我们不知道犯这类错误的概率p的大小,但是知道,若α越大,则p越小
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
根据列联表中的数据,经计算得到
根据小概率值=0.005的独立性检验,没有充分证据推断 H0不成立,因此可以认为 H0成立,即认为两种疗法效果没有差异.
追问1:若对调两种疗法的位置或对调两种疗效的位置,这样做会影响取值的计算结果吗?
不影响
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
疗法 疗效 合计
未治愈 治愈 乙 6 63 69
甲 15 52 67
合计 21 115 136
疗法 疗效 合计
治愈 未治愈 甲 52 15 67
乙 63 6 69
合计 115 21 136
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
追问2:根据小概率值=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效 合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
根据小概率值=0.05的独立性检验,我们推断 H0不成立,即可以认为两种疗法效果有差异,该推断犯错误的概率不超过0.05.
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
根据列联表中的数据,经计算得到
追问2:根据小概率值=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:
甲种疗法未治愈和治愈的频率分别是和
乙种疗法未治愈和治愈的频率分别是和0.913.
因此可以推断乙种疗法的效果比甲种疗法好。
例:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
例4:为了调查吸烟是否对肺癌有影响,某肿瘤研究所采取有放回简单随机抽样,调查了9965人,得到如下结果(单位:人)依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险。
解:零假设为H0:吸烟和患肺癌之间没有关系根据列联表中的数据,经计算的
χ2 =
>
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为吸 烟与患肺癌有关联,此推断犯错误的概率不大于0.001,即我们有99.9%的把握认为“吸烟与患肺癌有关系”.
吸烟 肺癌 合计
非肺癌患者 肺癌患者 非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
根据表中的数据计算不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的评率分别为
由
可见,在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌频率的4倍以上。于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌概率,即吸烟更容易引发肺癌。
方法总结
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
应用独立性检验解决实际问题大致应包括以下几个主要环节:
注意:上述几个环节的内容可以根据不同情况进行调整,
例如,在有些时候,分类变量的抽样数据列联表是问题中给定的.
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
0.1%把握认
为A与B无关
1%把握认为A与B无关
99.9%把握认
为A与B有关
99%把握认
为A与B有关
90%把握认
为A与B有关
10%把握认为
A与B无关
没有充分的依据显示A与B有关,但也不能显示A与B无关
例如
学习新知
在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示。问:该种血清能否起到预防感冒的作用?
未感冒 感冒 合计
使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1000
解:设H0:感冒与是否使用该血清没有关系。
因当H0成立时, χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用。
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
典型例题
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
有效 无效 合计
口服 58 40 98
注射 64 31 95
合计 122 71 193
解:设H0:药的效果与给药方式没有关系。
因当H0成立时, 2≥1.3896的概率大于15%,故不能否定假设H0,即不能作出药的效果与给药方式有关的结论。
<2.072
为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查的结果列在表中,根据所选择的193个病人的数据,能否作出药的效果和给药方式有关的结论?
典型例题
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
气管炎是一种常见的呼吸道疾病,医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比,所得数据如表所示,问:它们的疗效有无差异?
有效 无效 合计
复方江剪刀草 184 61 245
胆黄片 91 9 100
合计 275 70 345
解:设H0:两种中草药的治疗效果没有差异。
因当H0成立时, 2≥10.828的概率为0.001,故有99.9%的把握认为,两种药物的疗效有差异。
典型例题
某校对学生的课外活动进行调查,结果整理成下表:
体育 文娱 总计
男生 21 23 44
女生 6 29 35
总计 27 52 79
试用你所学过的知识分析:能否在犯错误的概率不超过0.005的前提下,认为“喜欢体育还是文娱与性别有关系”?
巩固练习
∵a=21,b=23,c=6,d=29,n=79,
即我们得到的K2的观测值k≈8.106超过7.879这就意味着:“喜欢体育还是文娱与性别没有关系”这一结论成立的可能性小于0.005,即在犯错误的概率不超过0.005的前提下认为“喜欢体育还是喜欢文娱与性别有关.”
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
巩固练习
某县城区常见在合法的广告牌上又贴有违法的黑广告,城管对此进行了清理,并下了通告.一周后,城管对某街道进行了检查.作了如下统计:
贴有黑广告 未贴有黑广告 总计
通告前 39 157 196
通告后 29 167 196
总计 68 324 392
请你判断,城管下通告对减少黑广告数是否有效?
巩固练习
巩固练习
C
先假设两个分类变量X与Y无关系,利用上述公式根据观测数据求出K2的观测值k,再得出X与Y有关系的程度.
(1)如果k≥10.828,就有______的把握认为“X与Y有关系” (2)如果k≥7.879,就有______的把握认为“X与Y有关系”;
99.9%
99.5%
(3)如果k≥_____,就有99%的把握认为“X与Y有关系” (4)如果k≥5.024,就有97.5%的把握认为“X与Y有关系” (5)如果k≥3.841,就有_____的把握认为“X与Y有关系” (6)如果k≥2.706,就有_____的把握认为“X与Y有关系”.
6.635
95%
90%
课堂小结
不渴望能够一跃千里,只希望每天能够前进一步。
1.分类变量X和Y的抽样数据的2×2列联表:
课堂小结
2.独立性检验的一般步骤:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释. (2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较. (3)根据检验规则得出推断结论. (4)在X和Y不独立的情况下,根据需要,通过比较相应的频率, 分析X和Y间的影响规律.
n=a+b+c+d
b+d
a+c
合计
c+d
d
c
X=1
a+b
b
a
X=0
Y=1
Y=0
合计
Y
X
