24.1.2 垂直于弦的直径 学案
图片预览



文档简介
中小学教育资源及组卷应用平台
24.1.2 垂直于弦的直径 学案
课题 24.1.2 垂直于弦的直径 单元 第23单元 学科 数学 年级 九年级上册
学习目标 1.进一步认识圆,了解圆是轴对称图形.2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.3.灵活运用垂径定理解决有关圆的问题.
重点 1.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.2.灵活运用垂径定理解决有关圆的问题.
难点 灵活运用垂径定理解决有关圆的问题.
教学过程
导入新课 【引入思考】 环节一:探究圆的轴对称性剪一张圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明你的结论吗?猜想:圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.求证:圆是轴对称图形. 分析:要证明圆是轴对称图形,只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.环节二:探究垂径定理及推论如图, 把圆沿着直径CD折叠时,除了点A与点A'重合之外,还有哪些相等的线段和弧?试一试证明你的发现!你能用文字语言、符号语言归纳出上述结论吗?(1)垂径定理: (2)符号语言:∵是⊙的 又∵ ∴ = ; =_________ 我们把这个定理分成几个结论分别有:①CD是直径、AB是弦,②CD⊥AB③AE=BE④=⑤我们知道①②可以推出结论③④⑤,那么如果交换符号结论是否有更多的结论成立?试一试:例如:① 直径过圆心 ③ 平分弦推出② 垂直于弦④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧证明这个结论。形成推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.已知:AB不是直径,CD过圆心 ,AM=BM结论:CD⊥AB,AD=BD,AC=BC类比推论1你可以写出相应的命题吗 相信自己是最棒的!小组之间讨论思考:为什么平分的弦不是直径?如果弦AB是过圆心的弦呢 平分弦AB的直径CD一定会垂直弦AB吗?垂径定理中出现的常见三角形,用于计算:在a,d,r,h中,已知其中任意两个量,可以求出其它两个量.
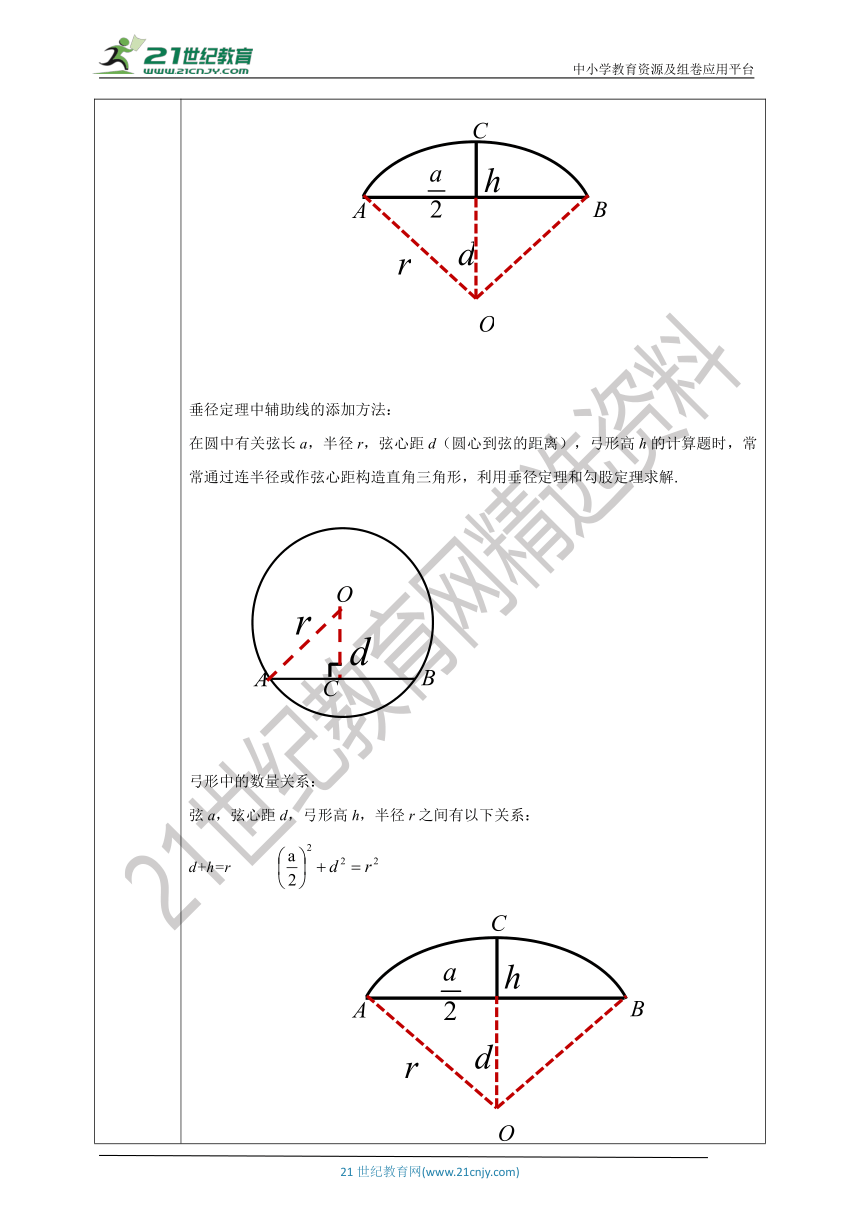
新知讲解 提炼概念根据垂径定理与推论可知对于一个圆和一条直线来说,如果具备:(1)过圆心(2)垂直于弦(3)平分弦(非直径)(4)平分弦所对的优弧(5)平分弦所对的劣弧上述五个条件中的任意两个条件,都可以推出其他三个结论.(知二推三)典例精讲 例2 赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m. 求赵州桥主桥拱的半径(结果保留小数点后一位). 垂径定理中辅助线的添加方法:在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.弓形中的数量关系:弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r
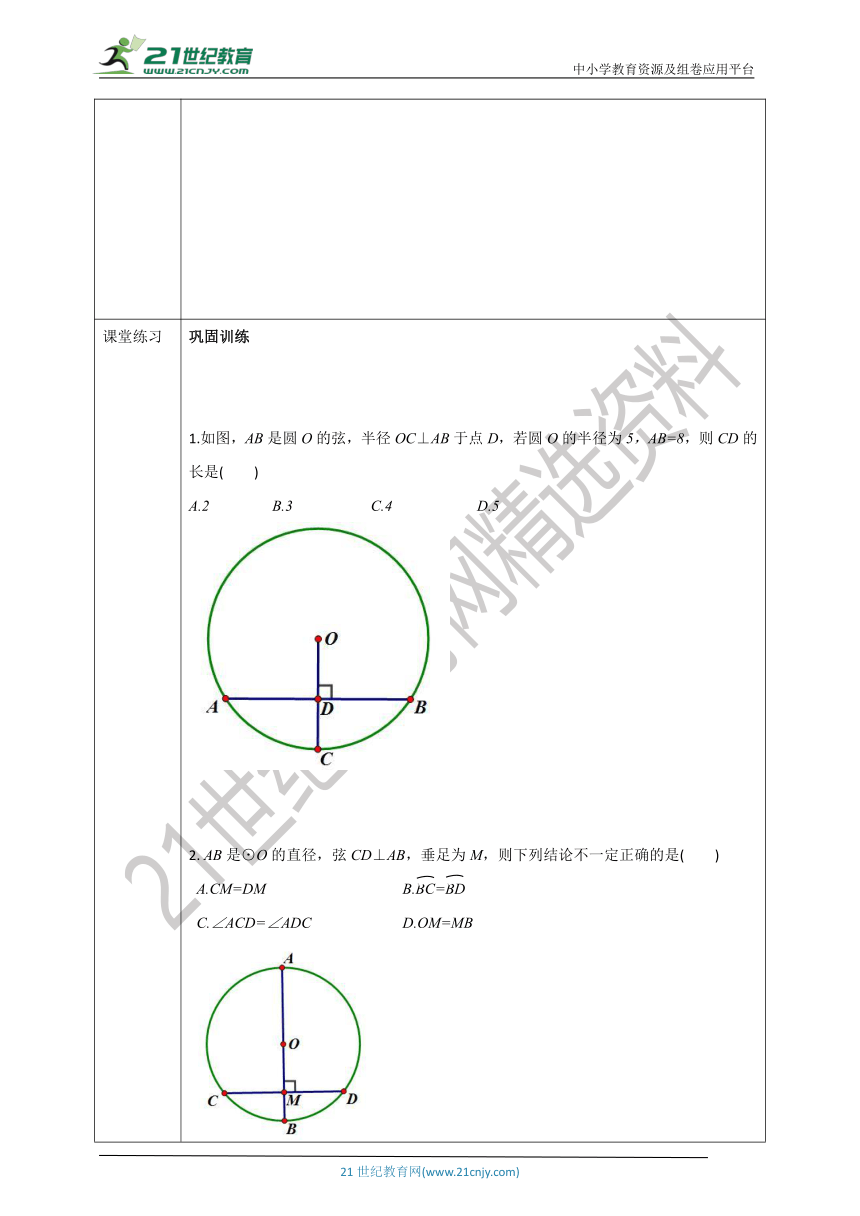
课堂练习 巩固训练 1.如图,AB是圆O的弦,半径OC⊥AB于点D,若圆O的半径为5,AB=8,则CD的长是( )A.2 B.3 C.4 D.52. AB是⊙O的直径,弦CD⊥AB,垂足为M,则下列结论不一定正确的是( ) A.CM=DM B.BC=BD C.∠ACD=∠ADC D.OM=MB3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC= 2cm,求半径OC的长.4.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.5.已知圆O的半径为10 cm,AB,CD是圆O的两条弦,AB//CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是多少?分析:弦AB、CD可能在圆心的同侧,也可能在圆心的异侧. 分类讨论 答案引入思考环节一证明:如图,CD是⊙O的任意一条直径,AA ′是弦,使AA′⊥CD,垂足为M连接OA,OA′,则OA=OA′.∵AA′⊥CD,∴CD是AA′的垂直平分线.∴对于圆上任意一点A,在圆上都有关于直线CD的对称点A′,即⊙O关于直线CD对称.圆的对称性:圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.注意:不能说圆的直径是圆的对称轴,因为对称轴是直线,而直径是线段.环节二:探究垂径定理及推论如图, 把圆沿着直径CD折叠时,除了点A与点A'重合之外,还有哪些相等的线段和弧?AM=A'M,AD=A'D,AC=A'C直径CD平分弦AA',并且平分AA' ,A'CA垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理的几个基本图形:如图, ⊙O的直径CD垂直于弦AB,垂足为M. 仔细观察,图形中有哪些相等的线段和弧?为什么?已知:CD是直径,CD⊥AB 结论:AM=A'M,AD=A'D,AC=A'C垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.已知:AB不是直径,CD过圆心 ,AM=BM结论:CD⊥AB,AD=BD,AC=BC思考:为什么平分的弦不是直径?如果弦AB是过圆心的弦呢 平分弦AB的直径CD一定会垂直弦AB吗?不会提炼概念 典例精讲 n-m例 例2 解:过点O作OC⊥AB,连接OA. 如图,设赵州桥主桥拱的半径为R m.由题意,可知AB=37m,CD=7.23m,则AD=18.5m,OD=R-7.23在Rt△OAD中,由勾股定理得R2=18.52+(R-7.23)2.解得R≈27.3.因此,赵州桥的主桥拱半径约为27.3 m.垂径定理中辅助线的添加方法:在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.弓形中的数量关系:弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r 巩固训练AD4.解 设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,5. 解:分两种情况进行讨论:①当弦AB和CD在圆心同侧时,如图1,过点O作OF⊥CD,垂足为F,交AB于点E,连接OC,OA.∵ AB//CD,∴OE⊥AB.∵AB=16cm,CD=12cm,∴AE=8cm,CF=6cm,∵OA=OC=10cm,由勾股定理,得EO=6cm,OF=8cm,∴EF=OF-OE=2 cm.②当弦AB和CD在圆心异侧时,过点O作OE⊥CD,交CD于点E,延长EO交AB于点F,连接OC、OA,如图2所示∵ AB//CD,∴ OF⊥AB∵AB=16cm,CD=12cm,∴AF=8cm,CE=6cm.∵OA=OC=10cm,由勾股定理,得OE=8cm,OF=6cm, ∴EF=OF+OE=14cm.综上所述:AB和CD之间的距离为2cm或14cm.
课堂小结
A
B
C
D
O
h
r
d
A
B
C
d
O
r
A
B
C
D
O
h
r
d
A
B
C
D
O
h
r
d
A
B
C
d
O
r
A
B
C
D
O
h
r
d
垂直于弦的直径平分弦,并且平分弦所对的两条弧
内容
①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.
推论
连半径,作弦心距
辅助线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.1.2 垂直于弦的直径 学案
课题 24.1.2 垂直于弦的直径 单元 第23单元 学科 数学 年级 九年级上册
学习目标 1.进一步认识圆,了解圆是轴对称图形.2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.3.灵活运用垂径定理解决有关圆的问题.
重点 1.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.2.灵活运用垂径定理解决有关圆的问题.
难点 灵活运用垂径定理解决有关圆的问题.
教学过程
导入新课 【引入思考】 环节一:探究圆的轴对称性剪一张圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明你的结论吗?猜想:圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.求证:圆是轴对称图形. 分析:要证明圆是轴对称图形,只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.环节二:探究垂径定理及推论如图, 把圆沿着直径CD折叠时,除了点A与点A'重合之外,还有哪些相等的线段和弧?试一试证明你的发现!你能用文字语言、符号语言归纳出上述结论吗?(1)垂径定理: (2)符号语言:∵是⊙的 又∵ ∴ = ; =_________ 我们把这个定理分成几个结论分别有:①CD是直径、AB是弦,②CD⊥AB③AE=BE④=⑤我们知道①②可以推出结论③④⑤,那么如果交换符号结论是否有更多的结论成立?试一试:例如:① 直径过圆心 ③ 平分弦推出② 垂直于弦④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧证明这个结论。形成推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.已知:AB不是直径,CD过圆心 ,AM=BM结论:CD⊥AB,AD=BD,AC=BC类比推论1你可以写出相应的命题吗 相信自己是最棒的!小组之间讨论思考:为什么平分的弦不是直径?如果弦AB是过圆心的弦呢 平分弦AB的直径CD一定会垂直弦AB吗?垂径定理中出现的常见三角形,用于计算:在a,d,r,h中,已知其中任意两个量,可以求出其它两个量.
新知讲解 提炼概念根据垂径定理与推论可知对于一个圆和一条直线来说,如果具备:(1)过圆心(2)垂直于弦(3)平分弦(非直径)(4)平分弦所对的优弧(5)平分弦所对的劣弧上述五个条件中的任意两个条件,都可以推出其他三个结论.(知二推三)典例精讲 例2 赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m. 求赵州桥主桥拱的半径(结果保留小数点后一位). 垂径定理中辅助线的添加方法:在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.弓形中的数量关系:弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r
课堂练习 巩固训练 1.如图,AB是圆O的弦,半径OC⊥AB于点D,若圆O的半径为5,AB=8,则CD的长是( )A.2 B.3 C.4 D.52. AB是⊙O的直径,弦CD⊥AB,垂足为M,则下列结论不一定正确的是( ) A.CM=DM B.BC=BD C.∠ACD=∠ADC D.OM=MB3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC= 2cm,求半径OC的长.4.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.5.已知圆O的半径为10 cm,AB,CD是圆O的两条弦,AB//CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是多少?分析:弦AB、CD可能在圆心的同侧,也可能在圆心的异侧. 分类讨论 答案引入思考环节一证明:如图,CD是⊙O的任意一条直径,AA ′是弦,使AA′⊥CD,垂足为M连接OA,OA′,则OA=OA′.∵AA′⊥CD,∴CD是AA′的垂直平分线.∴对于圆上任意一点A,在圆上都有关于直线CD的对称点A′,即⊙O关于直线CD对称.圆的对称性:圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.注意:不能说圆的直径是圆的对称轴,因为对称轴是直线,而直径是线段.环节二:探究垂径定理及推论如图, 把圆沿着直径CD折叠时,除了点A与点A'重合之外,还有哪些相等的线段和弧?AM=A'M,AD=A'D,AC=A'C直径CD平分弦AA',并且平分AA' ,A'CA垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理的几个基本图形:如图, ⊙O的直径CD垂直于弦AB,垂足为M. 仔细观察,图形中有哪些相等的线段和弧?为什么?已知:CD是直径,CD⊥AB 结论:AM=A'M,AD=A'D,AC=A'C垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.已知:AB不是直径,CD过圆心 ,AM=BM结论:CD⊥AB,AD=BD,AC=BC思考:为什么平分的弦不是直径?如果弦AB是过圆心的弦呢 平分弦AB的直径CD一定会垂直弦AB吗?不会提炼概念 典例精讲 n-m例 例2 解:过点O作OC⊥AB,连接OA. 如图,设赵州桥主桥拱的半径为R m.由题意,可知AB=37m,CD=7.23m,则AD=18.5m,OD=R-7.23在Rt△OAD中,由勾股定理得R2=18.52+(R-7.23)2.解得R≈27.3.因此,赵州桥的主桥拱半径约为27.3 m.垂径定理中辅助线的添加方法:在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.弓形中的数量关系:弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r 巩固训练AD4.解 设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,5. 解:分两种情况进行讨论:①当弦AB和CD在圆心同侧时,如图1,过点O作OF⊥CD,垂足为F,交AB于点E,连接OC,OA.∵ AB//CD,∴OE⊥AB.∵AB=16cm,CD=12cm,∴AE=8cm,CF=6cm,∵OA=OC=10cm,由勾股定理,得EO=6cm,OF=8cm,∴EF=OF-OE=2 cm.②当弦AB和CD在圆心异侧时,过点O作OE⊥CD,交CD于点E,延长EO交AB于点F,连接OC、OA,如图2所示∵ AB//CD,∴ OF⊥AB∵AB=16cm,CD=12cm,∴AF=8cm,CE=6cm.∵OA=OC=10cm,由勾股定理,得OE=8cm,OF=6cm, ∴EF=OF+OE=14cm.综上所述:AB和CD之间的距离为2cm或14cm.
课堂小结
A
B
C
D
O
h
r
d
A
B
C
d
O
r
A
B
C
D
O
h
r
d
A
B
C
D
O
h
r
d
A
B
C
d
O
r
A
B
C
D
O
h
r
d
垂直于弦的直径平分弦,并且平分弦所对的两条弧
内容
①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.
推论
连半径,作弦心距
辅助线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
