2018-2019学年河北省保定市冀教版五年级下册期末质量监测数学试卷(带答案解析)
文档属性
| 名称 | 2018-2019学年河北省保定市冀教版五年级下册期末质量监测数学试卷(带答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 522.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 11:25:36 | ||
图片预览


文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
绝密★启用前
2018-2019学年河北省保定市冀教版五年级下册期末质量监测数学试卷
试卷副标题
考试范围:xxx;考试时间:120分钟;命题人:xxx
题号 一 二 三 四 五 六 总分
得分
注意事项:
1、答题前填写好自己的姓名、班级、考号等信息
2、请将答案正确填写在答题卡上
评卷人得分
一、 填空题(共11题)
1. 在括号里填上合适的数。
3.07立方米=(________)立方米(________)立方分米
5080毫升=(________)升
立方分米=(________)立方厘米
2.
3. 填上合适的单位。
一盒粉笔的体积约是1(______)
一个鱼缸的体积约是0.5(______)
一瓶红酒的体积约是750 (______)
一个骰子的体积约是1(______)
4. 分母是9的最简真分数有(________)个,它们的和是(________),再添上(________)个这样的分数单位就成为最小的合数。
5. 比30千克多的是(______)千克;(______)米比60米少。
6. 已知,,如果、的最大公因数是21,那么是(________),和的最小公倍数是(________)。
7. “女生人数比男生人数少”,是把(______)看作单位“1”;“女生人数是男生人数的(______),男生人数占全班人数的(______)。
8. 把米长的绳子剪成同样长的小段,共剪了4次,剪下的每段绳子的长度占全长的(______),每段绳子长(______)米。
9. 一个长方体的棱长之和是64厘米,长是6厘米,宽是5厘米,它的体积是(________)立方厘米。
10. 把三个完全相同的小正方体拼成一个大长方体,表面积减少了120平方厘米,这个长方体的表面积是(______)平方厘米。
11. 一个正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍,体积就扩大到原来的6倍. .
评卷人得分
二、 计算题(共3题)
12. 在括号里填上“”“”或“”。
(______) (______) (______) (______)
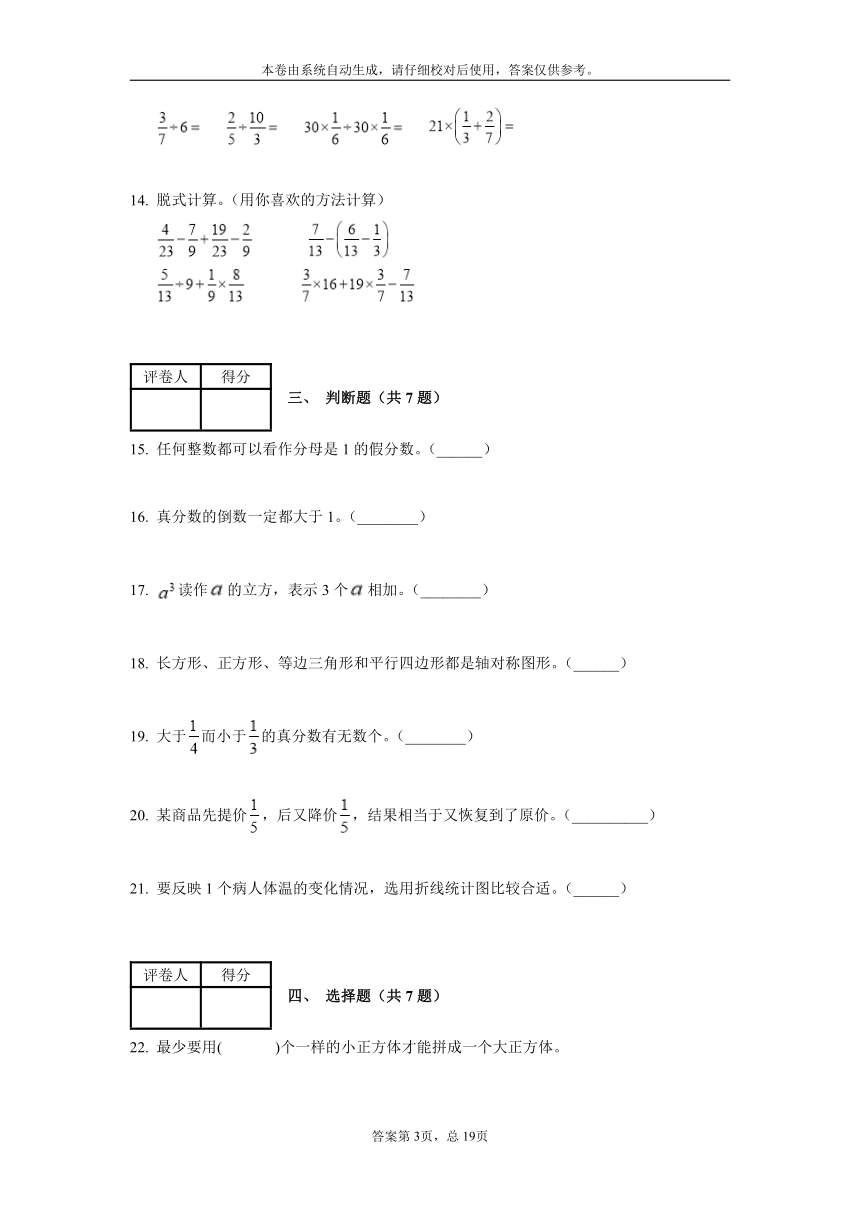
13. 直接写得数。
14. 脱式计算。(用你喜欢的方法计算)
评卷人得分
三、 判断题(共7题)
15. 任何整数都可以看作分母是1的假分数。(______)
16. 真分数的倒数一定都大于1。(________)
17. 读作的立方,表示3个相加。(________)
18. 长方形、正方形、等边三角形和平行四边形都是轴对称图形。(______)
19. 大于而小于的真分数有无数个。(________)
20. 某商品先提价,后又降价,结果相当于又恢复到了原价。(__________)
21. 要反映1个病人体温的变化情况,选用折线统计图比较合适。(______)
评卷人得分
四、 选择题(共7题)
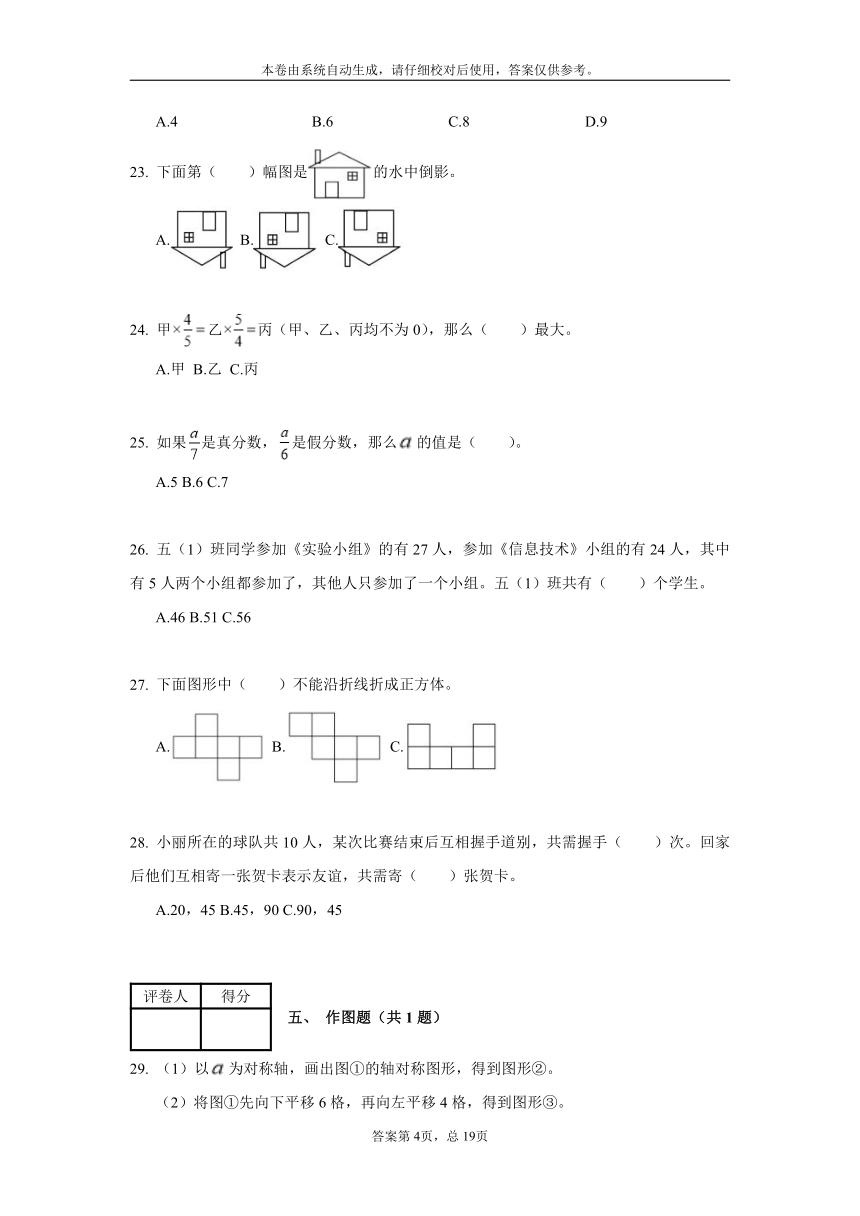
22. 最少要用( )个一样的小正方体才能拼成一个大正方体。
A.4 B.6 C.8 D.9
23. 下面第( )幅图是的水中倒影。
A. B. C.
24. 甲乙丙(甲、乙、丙均不为0),那么( )最大。
A.甲 B.乙 C.丙
25. 如果是真分数,是假分数,那么的值是( )。
A.5 B.6 C.7
26. 五(1)班同学参加《实验小组》的有27人,参加《信息技术》小组的有24人,其中有5人两个小组都参加了,其他人只参加了一个小组。五(1)班共有( )个学生。
A.46 B.51 C.56
27. 下面图形中( )不能沿折线折成正方体。
A. B. C.
28. 小丽所在的球队共10人,某次比赛结束后互相握手道别,共需握手( )次。回家后他们互相寄一张贺卡表示友谊,共需寄( )张贺卡。
A.20,45 B.45,90 C.90,45
评卷人得分
五、 作图题(共1题)
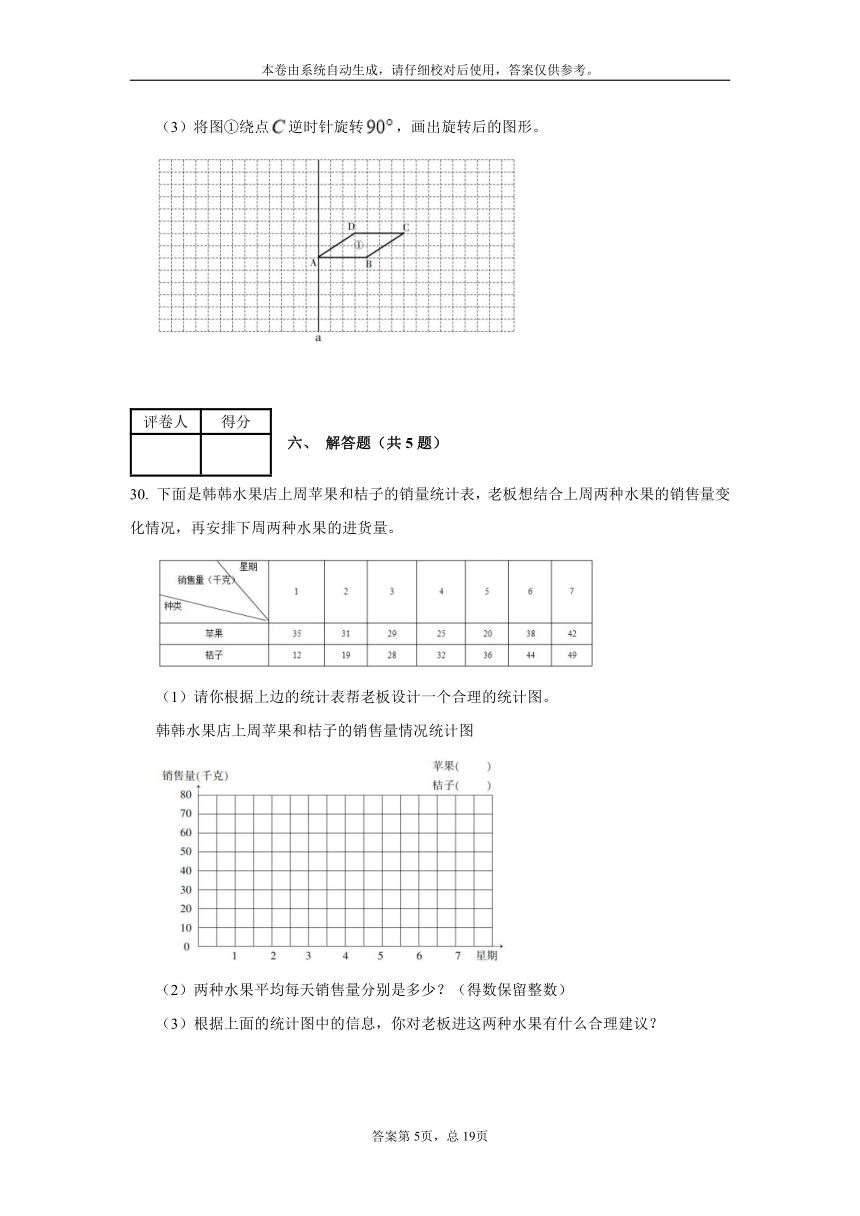
29. (1)以为对称轴,画出图①的轴对称图形,得到图形②。
(2)将图①先向下平移6格,再向左平移4格,得到图形③。
(3)将图①绕点逆时针旋转,画出旋转后的图形。
评卷人得分
六、 解答题(共5题)
30. 下面是韩韩水果店上周苹果和桔子的销量统计表,老板想结合上周两种水果的销售量变化情况,再安排下周两种水果的进货量。
(1)请你根据上边的统计表帮老板设计一个合理的统计图。
韩韩水果店上周苹果和桔子的销售量情况统计图
(2)两种水果平均每天销售量分别是多少?(得数保留整数)
(3)根据上面的统计图中的信息,你对老板进这两种水果有什么合理建议?
31. 某小学植树节植树,四年级植了60棵,五年级比四年级多植了,六年级植树棵树是五年级植树棵树的,六年级植树多少棵?
32. 修一条路,第一个月修了全长的,第二个月修了全长的,这时还剩下35千米。这条路全长多少千米?(先画线段图找出数量关系,再用方程解答。)
33. 某村要挖一个长方体蓄水池,这个蓄水池长24米、宽20米、深2米。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果再这个蓄水池的四周和底部贴上边长是4分米的方砖,需要多少块方砖?
(3)往池中注入深1.5米的水,池中水的体积是多少升?
34. 一辆汽车从甲地开往乙地,第一小时行了80千米,第二小时行了全程的,这时超过中点60千米。甲乙两地相距多少千米?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○………
)
试卷第2页,总2页
试卷第1页,总1页
参考答案及解析
一、 填空题
1. 【答案】
3 70 5.08 625
【解析】
1立方米=1000立方分米,1升=1000毫升,1立方分米=1000立方厘米,据此解答。
3.07立方米=3+0.07×1000=3立方米70立方分米
5080毫升=5080÷1000=5.08升
立方分米=×1000=625立方厘米
2. 【答案】
21;40;28
【解析】
根据被除数=商×除数,0.875×24=21;根据小数化成分数的方法,0.875==,根据分数的基本性质,==;==。
根据分析可知,21÷24=0.875==。
故答案为:21;40;28
3. 【答案】
立方分米 立方分米 立方厘米 立方厘米
【解析】
根据生活经验,对体积单位和数据的大小认识,可知计量一盒粉笔的体积用“立方分米”作单位;可知计量一个鱼缸的体积用“立方分米”作单位;可知计量一瓶红酒的体积用“立方厘米”作单位;可知计量一个骰子的体积用“立方厘米”作单位。
一盒粉笔的体积约是1立方分米;
一个鱼缸的体积约是0.5立方分米;
一瓶红酒的体积约是750立方厘米;
一个骰子的体积约是1立方厘米。
4. 【答案】
6 3 9
【解析】
分子分母互质的分数是最简分数,分子小于分母的分数是真分数,最小的合数是4,据此解答。
由分析可知,分母是9的最简真分数有:,有6个,,它们的和是3,4-3=1,1=,再添上9个这样的分数单位就成为最小的合数。
5. 【答案】
36 45
【解析】
把30千克看作单位“1”,求30千克的(1+)是多少,用乘法;
把60米看作单位“1”,求60米的(1-)是多少,用乘法。
30×(1+)
=30×
=36(千克)
60×(1-)
=60×
=45(米)
故答案为:36;45
6. 【答案】
7 630
【解析】
因为a和b公有的质因数有3和m,根据a和b最大的公因数是21,据此可以求出m的值;再把a和b公有的质因数和独有的质因数相乘,就可求出a和b的最小公倍数。
A和B的最大公因数是21,
所以3×m=21,则m=21÷3=7,
A和B最小的公倍数是2×3×3×5×7=630。
故答案为:7;630
7. 【答案】
男生人数
【解析】
“女生人数比男生人数少”,是把男生人数看作单位“1”,平均分成4份,女生是3份,3÷4=即为女生是男生的几分之几;全班人数是3+4=7(份),4÷7=即为男生人数占全班人数的几分之几。
根据分析可知,“女生人数比男生人数少”,是把(男生人数)看作单位“1”;“女生人数是男生人数的(),男生人数占全班人数的()。
故答案为:男生人数;;
8. 【答案】
【解析】
将绳子看成单位“1”,把单位“1”平均分成4份,每份是;求每段绳子的长度,用×即可解答。
1÷4=
×=(米)
9. 【答案】
150
【解析】
长方体的棱长之和=(长+宽+高)×4,长方体的体积=长×宽×高,据此解答即可。
64÷4=16(厘米)
16-(6+5)
=16-11
=5(厘米)
6×5×5=150(立方厘米)
故答案为:150
10. 【答案】
420
【解析】
把三个完全相同的小正方体拼成一个大长方体,表面积减少了4个面,由此可以求出正方体一个面的面积,进而用一个面的面积乘6求得原来正方体的表面积,再乘3求出三个正方体的表面积,最后再减120平方厘米即为这个长方体的表面积。
120÷4×6×3-120
=30×6×3-120
=540-120
=420(平方厘米)
故答案为:420
11. 【答案】
错误
试题分析:根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方,列式计算后再判断即可得到答案.
解:解:一个正方体棱长扩大2倍,则表面积扩大2×2=4倍,体积扩大2×2×2=8倍.
故答案为:错误.
【解析】
二、 计算题
12. 【答案】
< = > <
【解析】
(1)一个数乘以小于1的数,积小于这个数;
(2)甲数除以乙数(0除外),等于甲数乘乙数的倒数;
(3)一个数乘以大于1的数,积大于这个数;
< =6×4=24= > =<
13. 【答案】
;;18;;
;;;13
【解析】
(1)异分母分数相加减,需要先通分,再按同分母分数相加减,即分母不变,分子相加减;
(2)分数与分数相乘,分子与分子相乘做分子,分母与分母相乘做分母,能约分的要约分;
(3)分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答。
18
=
=
=
=7+6
=13
14. 【答案】
0;
;
【解析】
(1)根据加法交换律和加法结合律,将原式变为,然后进行计算即可;
(2)将原式去括号,变为,然后按照顺序计算即可;
(3)先将原式变为,然后根据乘法分配律逆运算,提取公因数,式子变为,然后计算即可;
(4)根据乘法分配律逆运算,提取公因数,式子变为,然后进行计算即可。
=
=1-1
=0
=
=
=
=
=
=
=
=
=
=
三、 判断题
15. 【答案】
×
【解析】
假分数的分子大于或等于分母,0是整数,但它不是假分数,据此解答。
根据分析可知,任何整数都可以看作分母是1的假分数,说法错误。
故答案为:×
16. 【答案】
√
【解析】
真分数都小于1,求一个数的倒数用1÷这个数即可。
因为真分数都小于1,1÷一个小于1的数(0除外),结果大于1,所以原题说法正确。
17. 【答案】
×
【解析】
读作的立方,表示3个a相乘,据此判断。
由分析可知=a×a×a,所以读作的立方,表示3个相加。说法错误。
故答案为:错误。
18. 【答案】
×
【解析】
根据平行四边形的性质可知,平行四边形不是轴对称图形。
根据分析可知,长方形、正方形、等边三角形都是轴对称图形,但平行四边形不是。
所以原题说法错误。
19. 【答案】
√
【解析】
根据分数的意义和性质、分数大小的比较判断即可。
把分母和分子同时乘以或除以2、3、4……,分数的大小不变,可以得出不同的分数。
所以判断错误。
20. 【答案】
×
【解析】
把某商品的原价看作单位“1”,提价后,商品的价格变成1+,后面的降价是在1+的价格基础上降价的,所以先提价和后面降价的单位“1”是不同的,据此算出现价,再与原价比较大小即可。
把某商品的原价看作单位“1”
1+=
-×
=-
=
<1,现价比原价低
所以判断错误。
21. 【答案】
√
【解析】
折线统计图:用不同位置的点表示数量的多少,并用折线的上升和下降表示数量的增减变化情况,据此解答。
要反映1个病人体温的变化情况,选用折线统计图比较合适。这种说法是正确的。
故答案为:√
四、 选择题
22. 【答案】
C
【解析】
23. 【答案】
C
【解析】
要求房子的水中倒影,其实就是求房子关于水面的轴对称图形,将房子的各点相对于水面进行对称标点,然后再连接即可解答。
通过观察房子的轴对称图形可知,通过比对烟筒、窗户、门的位置即可判断出C图正确。
故答案为:C
24. 【答案】
A
【解析】
可以用赋值法设甲乙丙=1(甲、乙、丙均不为0),分别求出甲、乙、丙的值比较即可。
设甲乙丙=1(甲、乙、丙均不为0),则甲=,乙=,丙=1,由此可知甲>丙>乙,甲最大。
故选择:A。
25. 【答案】
B
【解析】
如果是真分数,那么a小于7;如果是假分数,那么a大于或等于6,由此即可判断。
根据分析可知,a是小于7,大于或等于6的数,即是6。
故答案为:B
26. 【答案】
A
【解析】
根据题意可知,把参加《实验小组》和参加《信息技术》小组的人数加在一起时,则表示两组都参加的5人被加了两次,所以用两组人数之和再减去一个5才是全班的总人数。
27+24=51(人)
51-5=46(人)
故答案为:A
27. 【答案】
C
【解析】
根据正方体的展开图的类型,1-4-1型,2-3-1型,2-2-2型,3-3型,只有C不属于其中的类型,不能折成正方体,据此解答即可。
由分析可知,A是1-4-1型,B是2-3-1型,C不能折成正方体。故选择:C。
28. 【答案】
B
【解析】
10人互相握手道别,甲与乙的握手和乙与甲的握手是同一次的握手,故第一个人握9次;第二个人握8次,依次类推。互相寄贺卡,甲寄给乙的贺卡与乙寄给甲的贺卡不是同一张贺卡,故贺卡张数=需要握手的次数×2。
由分析可知握手次数:
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=45(次);
贺卡张数:
45×2=90(张)
共需握手45次,贺卡张数90张。
故选择:B
五、 作图题
29. 【答案】
【解析】
(1)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴垂直平分对称点的连线,在对称轴的另一边画出关键的几个对称点,然后首尾连接各对称点即可;
(2)把图①的各个顶点分别向下平移6格,再向左平移4格,再依次连接起来即可;
(3)以点C为旋转中心,把图①各顶点分别绕点C逆时针旋转90度后,再顺次连接
起来即可;
由分析画图如下:
六、 解答题
30. 【答案】
(1)
(2)31千克;31千克
(3)在一周的几天里,前几天可以多摆放些苹果,后几天多放些桔子。
【解析】
根据表格和题意,可知折线统计图比较合理,用总销量除以天数即可求出平均数。
(1)
(2)(35+31+29+25+20+38+42)÷7
=220÷7
≈31(千克)
(12+19+28+32+36+44+49)÷7
=220÷7
≈31(千克)
答:两种水果上周平均每天销量都是31千克。
(3)在一周的几天里,前几天可以多摆放些苹果,后几天多放些桔子。
31. 【答案】
63棵
【解析】
五年级植树颗数=四年级植树棵数×(1+),六年级植树棵数=五年级植树棵树×,据此解答。
60×(1+)×
=60××
=63(棵)
答:六年级植树63棵。
32. 【答案】
200千米
【解析】
根据题意画线段图:
数量关系为:第一个月修的千米数+第二个月修的千米数+35千米=这条路的全长,设这条路全长x千米,据此列方程解答。
作图如下:
解:设这条路全长x千米。
x+x+35=x
(1--)x=35
x=35
x=200
答:这条路全长200千米。
33. 【答案】
(1)480平方米
(2)4100块
(3)720000升
【解析】
(1)求占地面积,即是长方体的底面积,用长乘宽即可解答;
(2)求方砖块数,先求出去除上面积的长方体的表面积,然后除以4×4的方砖面积即可;
(3)根据长方形体积公式,长乘宽乘高即可解答。
(1)24×20=480(平方米)
答:这个蓄水池的占地面积是480平方米。
(2)24米=240分米,20米=200分米,2米=20分米
(240×200+240×20×2+200×20×2)÷(4×4)
=(48000+9600+8000)÷16
=65600÷16
=4100(块)
答:需要4100块方砖。
(3)480×1.5=720(立方米)=720000(升)
答:池中水的体积是720000升。
34. 【答案】
200千米
【解析】
设甲乙两地相距x千米,等量关系式:第一小时行的路程+第二小时行的路程=甲乙两地的距离×+60,据此列方程解答。
解:设甲乙两地相距x千米。
80+x=x+60
x-x=80-60
x=20
x=200
答:甲乙两地相距200千米。
答案第2页,总2页
答案第1页,总1页
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
绝密★启用前
2018-2019学年河北省保定市冀教版五年级下册期末质量监测数学试卷
试卷副标题
考试范围:xxx;考试时间:120分钟;命题人:xxx
题号 一 二 三 四 五 六 总分
得分
注意事项:
1、答题前填写好自己的姓名、班级、考号等信息
2、请将答案正确填写在答题卡上
评卷人得分
一、 填空题(共11题)
1. 在括号里填上合适的数。
3.07立方米=(________)立方米(________)立方分米
5080毫升=(________)升
立方分米=(________)立方厘米
2.
3. 填上合适的单位。
一盒粉笔的体积约是1(______)
一个鱼缸的体积约是0.5(______)
一瓶红酒的体积约是750 (______)
一个骰子的体积约是1(______)
4. 分母是9的最简真分数有(________)个,它们的和是(________),再添上(________)个这样的分数单位就成为最小的合数。
5. 比30千克多的是(______)千克;(______)米比60米少。
6. 已知,,如果、的最大公因数是21,那么是(________),和的最小公倍数是(________)。
7. “女生人数比男生人数少”,是把(______)看作单位“1”;“女生人数是男生人数的(______),男生人数占全班人数的(______)。
8. 把米长的绳子剪成同样长的小段,共剪了4次,剪下的每段绳子的长度占全长的(______),每段绳子长(______)米。
9. 一个长方体的棱长之和是64厘米,长是6厘米,宽是5厘米,它的体积是(________)立方厘米。
10. 把三个完全相同的小正方体拼成一个大长方体,表面积减少了120平方厘米,这个长方体的表面积是(______)平方厘米。
11. 一个正方体的棱长扩大到原来的2倍,表面积就扩大到原来的4倍,体积就扩大到原来的6倍. .
评卷人得分
二、 计算题(共3题)
12. 在括号里填上“”“”或“”。
(______) (______) (______) (______)
13. 直接写得数。
14. 脱式计算。(用你喜欢的方法计算)
评卷人得分
三、 判断题(共7题)
15. 任何整数都可以看作分母是1的假分数。(______)
16. 真分数的倒数一定都大于1。(________)
17. 读作的立方,表示3个相加。(________)
18. 长方形、正方形、等边三角形和平行四边形都是轴对称图形。(______)
19. 大于而小于的真分数有无数个。(________)
20. 某商品先提价,后又降价,结果相当于又恢复到了原价。(__________)
21. 要反映1个病人体温的变化情况,选用折线统计图比较合适。(______)
评卷人得分
四、 选择题(共7题)
22. 最少要用( )个一样的小正方体才能拼成一个大正方体。
A.4 B.6 C.8 D.9
23. 下面第( )幅图是的水中倒影。
A. B. C.
24. 甲乙丙(甲、乙、丙均不为0),那么( )最大。
A.甲 B.乙 C.丙
25. 如果是真分数,是假分数,那么的值是( )。
A.5 B.6 C.7
26. 五(1)班同学参加《实验小组》的有27人,参加《信息技术》小组的有24人,其中有5人两个小组都参加了,其他人只参加了一个小组。五(1)班共有( )个学生。
A.46 B.51 C.56
27. 下面图形中( )不能沿折线折成正方体。
A. B. C.
28. 小丽所在的球队共10人,某次比赛结束后互相握手道别,共需握手( )次。回家后他们互相寄一张贺卡表示友谊,共需寄( )张贺卡。
A.20,45 B.45,90 C.90,45
评卷人得分
五、 作图题(共1题)
29. (1)以为对称轴,画出图①的轴对称图形,得到图形②。
(2)将图①先向下平移6格,再向左平移4格,得到图形③。
(3)将图①绕点逆时针旋转,画出旋转后的图形。
评卷人得分
六、 解答题(共5题)
30. 下面是韩韩水果店上周苹果和桔子的销量统计表,老板想结合上周两种水果的销售量变化情况,再安排下周两种水果的进货量。
(1)请你根据上边的统计表帮老板设计一个合理的统计图。
韩韩水果店上周苹果和桔子的销售量情况统计图
(2)两种水果平均每天销售量分别是多少?(得数保留整数)
(3)根据上面的统计图中的信息,你对老板进这两种水果有什么合理建议?
31. 某小学植树节植树,四年级植了60棵,五年级比四年级多植了,六年级植树棵树是五年级植树棵树的,六年级植树多少棵?
32. 修一条路,第一个月修了全长的,第二个月修了全长的,这时还剩下35千米。这条路全长多少千米?(先画线段图找出数量关系,再用方程解答。)
33. 某村要挖一个长方体蓄水池,这个蓄水池长24米、宽20米、深2米。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果再这个蓄水池的四周和底部贴上边长是4分米的方砖,需要多少块方砖?
(3)往池中注入深1.5米的水,池中水的体积是多少升?
34. 一辆汽车从甲地开往乙地,第一小时行了80千米,第二小时行了全程的,这时超过中点60千米。甲乙两地相距多少千米?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○………
)
试卷第2页,总2页
试卷第1页,总1页
参考答案及解析
一、 填空题
1. 【答案】
3 70 5.08 625
【解析】
1立方米=1000立方分米,1升=1000毫升,1立方分米=1000立方厘米,据此解答。
3.07立方米=3+0.07×1000=3立方米70立方分米
5080毫升=5080÷1000=5.08升
立方分米=×1000=625立方厘米
2. 【答案】
21;40;28
【解析】
根据被除数=商×除数,0.875×24=21;根据小数化成分数的方法,0.875==,根据分数的基本性质,==;==。
根据分析可知,21÷24=0.875==。
故答案为:21;40;28
3. 【答案】
立方分米 立方分米 立方厘米 立方厘米
【解析】
根据生活经验,对体积单位和数据的大小认识,可知计量一盒粉笔的体积用“立方分米”作单位;可知计量一个鱼缸的体积用“立方分米”作单位;可知计量一瓶红酒的体积用“立方厘米”作单位;可知计量一个骰子的体积用“立方厘米”作单位。
一盒粉笔的体积约是1立方分米;
一个鱼缸的体积约是0.5立方分米;
一瓶红酒的体积约是750立方厘米;
一个骰子的体积约是1立方厘米。
4. 【答案】
6 3 9
【解析】
分子分母互质的分数是最简分数,分子小于分母的分数是真分数,最小的合数是4,据此解答。
由分析可知,分母是9的最简真分数有:,有6个,,它们的和是3,4-3=1,1=,再添上9个这样的分数单位就成为最小的合数。
5. 【答案】
36 45
【解析】
把30千克看作单位“1”,求30千克的(1+)是多少,用乘法;
把60米看作单位“1”,求60米的(1-)是多少,用乘法。
30×(1+)
=30×
=36(千克)
60×(1-)
=60×
=45(米)
故答案为:36;45
6. 【答案】
7 630
【解析】
因为a和b公有的质因数有3和m,根据a和b最大的公因数是21,据此可以求出m的值;再把a和b公有的质因数和独有的质因数相乘,就可求出a和b的最小公倍数。
A和B的最大公因数是21,
所以3×m=21,则m=21÷3=7,
A和B最小的公倍数是2×3×3×5×7=630。
故答案为:7;630
7. 【答案】
男生人数
【解析】
“女生人数比男生人数少”,是把男生人数看作单位“1”,平均分成4份,女生是3份,3÷4=即为女生是男生的几分之几;全班人数是3+4=7(份),4÷7=即为男生人数占全班人数的几分之几。
根据分析可知,“女生人数比男生人数少”,是把(男生人数)看作单位“1”;“女生人数是男生人数的(),男生人数占全班人数的()。
故答案为:男生人数;;
8. 【答案】
【解析】
将绳子看成单位“1”,把单位“1”平均分成4份,每份是;求每段绳子的长度,用×即可解答。
1÷4=
×=(米)
9. 【答案】
150
【解析】
长方体的棱长之和=(长+宽+高)×4,长方体的体积=长×宽×高,据此解答即可。
64÷4=16(厘米)
16-(6+5)
=16-11
=5(厘米)
6×5×5=150(立方厘米)
故答案为:150
10. 【答案】
420
【解析】
把三个完全相同的小正方体拼成一个大长方体,表面积减少了4个面,由此可以求出正方体一个面的面积,进而用一个面的面积乘6求得原来正方体的表面积,再乘3求出三个正方体的表面积,最后再减120平方厘米即为这个长方体的表面积。
120÷4×6×3-120
=30×6×3-120
=540-120
=420(平方厘米)
故答案为:420
11. 【答案】
错误
试题分析:根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方,列式计算后再判断即可得到答案.
解:解:一个正方体棱长扩大2倍,则表面积扩大2×2=4倍,体积扩大2×2×2=8倍.
故答案为:错误.
【解析】
二、 计算题
12. 【答案】
< = > <
【解析】
(1)一个数乘以小于1的数,积小于这个数;
(2)甲数除以乙数(0除外),等于甲数乘乙数的倒数;
(3)一个数乘以大于1的数,积大于这个数;
< =6×4=24= > =<
13. 【答案】
;;18;;
;;;13
【解析】
(1)异分母分数相加减,需要先通分,再按同分母分数相加减,即分母不变,分子相加减;
(2)分数与分数相乘,分子与分子相乘做分子,分母与分母相乘做分母,能约分的要约分;
(3)分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答。
18
=
=
=
=7+6
=13
14. 【答案】
0;
;
【解析】
(1)根据加法交换律和加法结合律,将原式变为,然后进行计算即可;
(2)将原式去括号,变为,然后按照顺序计算即可;
(3)先将原式变为,然后根据乘法分配律逆运算,提取公因数,式子变为,然后计算即可;
(4)根据乘法分配律逆运算,提取公因数,式子变为,然后进行计算即可。
=
=1-1
=0
=
=
=
=
=
=
=
=
=
=
三、 判断题
15. 【答案】
×
【解析】
假分数的分子大于或等于分母,0是整数,但它不是假分数,据此解答。
根据分析可知,任何整数都可以看作分母是1的假分数,说法错误。
故答案为:×
16. 【答案】
√
【解析】
真分数都小于1,求一个数的倒数用1÷这个数即可。
因为真分数都小于1,1÷一个小于1的数(0除外),结果大于1,所以原题说法正确。
17. 【答案】
×
【解析】
读作的立方,表示3个a相乘,据此判断。
由分析可知=a×a×a,所以读作的立方,表示3个相加。说法错误。
故答案为:错误。
18. 【答案】
×
【解析】
根据平行四边形的性质可知,平行四边形不是轴对称图形。
根据分析可知,长方形、正方形、等边三角形都是轴对称图形,但平行四边形不是。
所以原题说法错误。
19. 【答案】
√
【解析】
根据分数的意义和性质、分数大小的比较判断即可。
把分母和分子同时乘以或除以2、3、4……,分数的大小不变,可以得出不同的分数。
所以判断错误。
20. 【答案】
×
【解析】
把某商品的原价看作单位“1”,提价后,商品的价格变成1+,后面的降价是在1+的价格基础上降价的,所以先提价和后面降价的单位“1”是不同的,据此算出现价,再与原价比较大小即可。
把某商品的原价看作单位“1”
1+=
-×
=-
=
<1,现价比原价低
所以判断错误。
21. 【答案】
√
【解析】
折线统计图:用不同位置的点表示数量的多少,并用折线的上升和下降表示数量的增减变化情况,据此解答。
要反映1个病人体温的变化情况,选用折线统计图比较合适。这种说法是正确的。
故答案为:√
四、 选择题
22. 【答案】
C
【解析】
23. 【答案】
C
【解析】
要求房子的水中倒影,其实就是求房子关于水面的轴对称图形,将房子的各点相对于水面进行对称标点,然后再连接即可解答。
通过观察房子的轴对称图形可知,通过比对烟筒、窗户、门的位置即可判断出C图正确。
故答案为:C
24. 【答案】
A
【解析】
可以用赋值法设甲乙丙=1(甲、乙、丙均不为0),分别求出甲、乙、丙的值比较即可。
设甲乙丙=1(甲、乙、丙均不为0),则甲=,乙=,丙=1,由此可知甲>丙>乙,甲最大。
故选择:A。
25. 【答案】
B
【解析】
如果是真分数,那么a小于7;如果是假分数,那么a大于或等于6,由此即可判断。
根据分析可知,a是小于7,大于或等于6的数,即是6。
故答案为:B
26. 【答案】
A
【解析】
根据题意可知,把参加《实验小组》和参加《信息技术》小组的人数加在一起时,则表示两组都参加的5人被加了两次,所以用两组人数之和再减去一个5才是全班的总人数。
27+24=51(人)
51-5=46(人)
故答案为:A
27. 【答案】
C
【解析】
根据正方体的展开图的类型,1-4-1型,2-3-1型,2-2-2型,3-3型,只有C不属于其中的类型,不能折成正方体,据此解答即可。
由分析可知,A是1-4-1型,B是2-3-1型,C不能折成正方体。故选择:C。
28. 【答案】
B
【解析】
10人互相握手道别,甲与乙的握手和乙与甲的握手是同一次的握手,故第一个人握9次;第二个人握8次,依次类推。互相寄贺卡,甲寄给乙的贺卡与乙寄给甲的贺卡不是同一张贺卡,故贺卡张数=需要握手的次数×2。
由分析可知握手次数:
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=45(次);
贺卡张数:
45×2=90(张)
共需握手45次,贺卡张数90张。
故选择:B
五、 作图题
29. 【答案】
【解析】
(1)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴垂直平分对称点的连线,在对称轴的另一边画出关键的几个对称点,然后首尾连接各对称点即可;
(2)把图①的各个顶点分别向下平移6格,再向左平移4格,再依次连接起来即可;
(3)以点C为旋转中心,把图①各顶点分别绕点C逆时针旋转90度后,再顺次连接
起来即可;
由分析画图如下:
六、 解答题
30. 【答案】
(1)
(2)31千克;31千克
(3)在一周的几天里,前几天可以多摆放些苹果,后几天多放些桔子。
【解析】
根据表格和题意,可知折线统计图比较合理,用总销量除以天数即可求出平均数。
(1)
(2)(35+31+29+25+20+38+42)÷7
=220÷7
≈31(千克)
(12+19+28+32+36+44+49)÷7
=220÷7
≈31(千克)
答:两种水果上周平均每天销量都是31千克。
(3)在一周的几天里,前几天可以多摆放些苹果,后几天多放些桔子。
31. 【答案】
63棵
【解析】
五年级植树颗数=四年级植树棵数×(1+),六年级植树棵数=五年级植树棵树×,据此解答。
60×(1+)×
=60××
=63(棵)
答:六年级植树63棵。
32. 【答案】
200千米
【解析】
根据题意画线段图:
数量关系为:第一个月修的千米数+第二个月修的千米数+35千米=这条路的全长,设这条路全长x千米,据此列方程解答。
作图如下:
解:设这条路全长x千米。
x+x+35=x
(1--)x=35
x=35
x=200
答:这条路全长200千米。
33. 【答案】
(1)480平方米
(2)4100块
(3)720000升
【解析】
(1)求占地面积,即是长方体的底面积,用长乘宽即可解答;
(2)求方砖块数,先求出去除上面积的长方体的表面积,然后除以4×4的方砖面积即可;
(3)根据长方形体积公式,长乘宽乘高即可解答。
(1)24×20=480(平方米)
答:这个蓄水池的占地面积是480平方米。
(2)24米=240分米,20米=200分米,2米=20分米
(240×200+240×20×2+200×20×2)÷(4×4)
=(48000+9600+8000)÷16
=65600÷16
=4100(块)
答:需要4100块方砖。
(3)480×1.5=720(立方米)=720000(升)
答:池中水的体积是720000升。
34. 【答案】
200千米
【解析】
设甲乙两地相距x千米,等量关系式:第一小时行的路程+第二小时行的路程=甲乙两地的距离×+60,据此列方程解答。
解:设甲乙两地相距x千米。
80+x=x+60
x-x=80-60
x=20
x=200
答:甲乙两地相距200千米。
答案第2页,总2页
答案第1页,总1页
同课章节目录
