人教A版(2019)选择性必修第一册2.1.2两条直线平行与垂直的判定 课件(共15张ppt)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册2.1.2两条直线平行与垂直的判定 课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 00:00:00 | ||
图片预览




文档简介
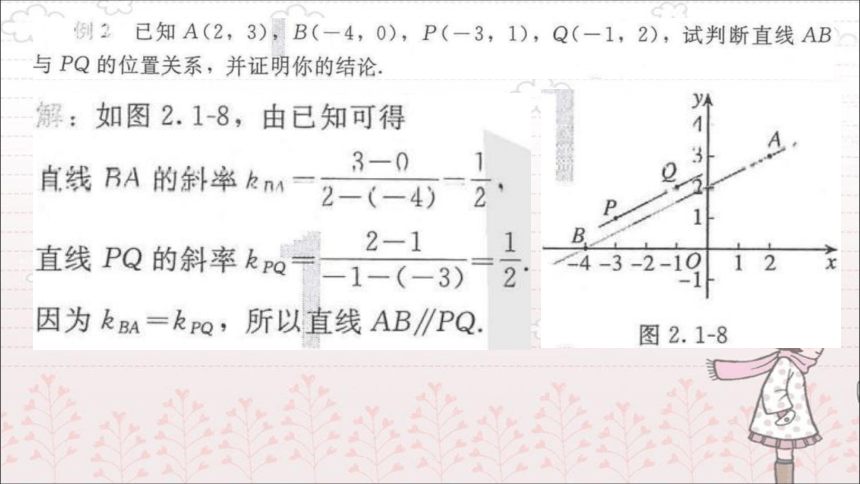
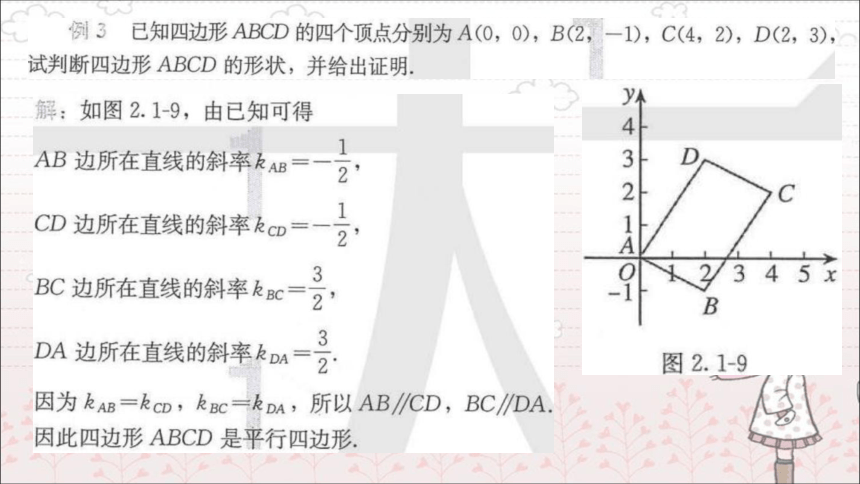
(共15张PPT)
2.1.2 两条直线平行与垂直的判定
学习目标:1min
1、理解并掌握两条直线平行及垂直的等价条件.
2.能应用两条直线平行或垂直的判定与性质解决一些简单问题.
问题导学:8min
1.直线的倾斜角和斜率的含义分别是什么?经过两点的直线的斜率公式是什么?
2.在平面直角坐标系中,平行与垂直是两条不同直线的两种特殊位置关系.
能不能通过直线的斜率来判定这两种位置关系呢?
O
y
x
l1
l2
α1
α2
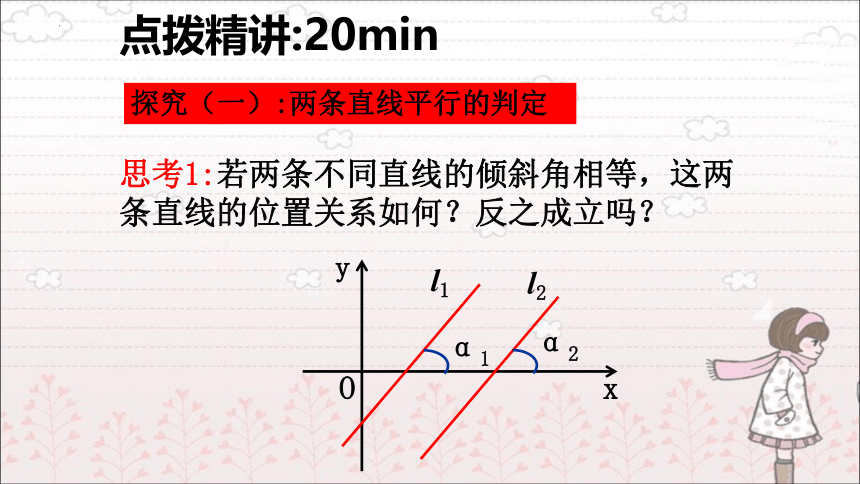
思考1:若两条不同直线的倾斜角相等,这两条直线的位置关系如何?反之成立吗?
探究(一):两条直线平行的判定
点拨精讲:20min
思考2:若两条不同直线的斜率相等,这两条直线的位置关系如何?反之成立吗?
思考3:对于两条不重合的直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
探究(二):两条直线垂直的判定
思考1:如图,设直线l1与l2的倾斜角分别为α1与α2,且α1<α2,若l1⊥l2,则α1与α2之间有什么关系?
y
l1
O
x
l2
α1
α2
思考3:反过来,当k1·k2 =-1时,直线l1与l2一定垂直吗?
思考2:你能得出直线l1与l2的斜率k1,k2之间的关系吗?
y
l1
O
x
l2
α1
α2
思考5:对任意两条直线,如果l1⊥l2,一定有k1·k2 =-1吗?
思考4:对于直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
1.两条直线的平行:
课堂小结:1min
l1∥l2 k1=k2
前提条件:①l1和l2是两条不重合的直线;
②l1和l2的斜率都存在.少了任何一个都会导致结论有误.
2.两条直线的垂直:
(1)当直线l1⊥直线l2时,它们斜率之间的关系有下列两种情况:
①它们的斜率都存在且乘积为定值-1;
②一条直线的斜率不存在,而另一条直线的斜率为0.
1.直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为( )
A.(3,0) B.(-3,0) C.(0,-3) D.(0,3)
2.若点P(a,b)与Q(b-1,a+1)关于直线l对称,则l的倾斜角为
( )
A.135° B.45° C.30° D.60°
当 堂 检测:15min
4.已知△ABC的三个顶点的坐标分别为A(-1,0),B(2,0),C(2,3).
(1)试判断△ABC的形状;
(2)求此三角形三条边上的高所在直线的斜率
D
B
a=-6
(直角三角形)
BC上的高K=0,AB上的高斜率不存在,AC边上的高K=-1
选做:已知长方形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2).求第四个顶点D的坐标.
2.1.2 两条直线平行与垂直的判定
学习目标:1min
1、理解并掌握两条直线平行及垂直的等价条件.
2.能应用两条直线平行或垂直的判定与性质解决一些简单问题.
问题导学:8min
1.直线的倾斜角和斜率的含义分别是什么?经过两点的直线的斜率公式是什么?
2.在平面直角坐标系中,平行与垂直是两条不同直线的两种特殊位置关系.
能不能通过直线的斜率来判定这两种位置关系呢?
O
y
x
l1
l2
α1
α2
思考1:若两条不同直线的倾斜角相等,这两条直线的位置关系如何?反之成立吗?
探究(一):两条直线平行的判定
点拨精讲:20min
思考2:若两条不同直线的斜率相等,这两条直线的位置关系如何?反之成立吗?
思考3:对于两条不重合的直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
探究(二):两条直线垂直的判定
思考1:如图,设直线l1与l2的倾斜角分别为α1与α2,且α1<α2,若l1⊥l2,则α1与α2之间有什么关系?
y
l1
O
x
l2
α1
α2
思考3:反过来,当k1·k2 =-1时,直线l1与l2一定垂直吗?
思考2:你能得出直线l1与l2的斜率k1,k2之间的关系吗?
y
l1
O
x
l2
α1
α2
思考5:对任意两条直线,如果l1⊥l2,一定有k1·k2 =-1吗?
思考4:对于直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
1.两条直线的平行:
课堂小结:1min
l1∥l2 k1=k2
前提条件:①l1和l2是两条不重合的直线;
②l1和l2的斜率都存在.少了任何一个都会导致结论有误.
2.两条直线的垂直:
(1)当直线l1⊥直线l2时,它们斜率之间的关系有下列两种情况:
①它们的斜率都存在且乘积为定值-1;
②一条直线的斜率不存在,而另一条直线的斜率为0.
1.直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为( )
A.(3,0) B.(-3,0) C.(0,-3) D.(0,3)
2.若点P(a,b)与Q(b-1,a+1)关于直线l对称,则l的倾斜角为
( )
A.135° B.45° C.30° D.60°
当 堂 检测:15min
4.已知△ABC的三个顶点的坐标分别为A(-1,0),B(2,0),C(2,3).
(1)试判断△ABC的形状;
(2)求此三角形三条边上的高所在直线的斜率
D
B
a=-6
(直角三角形)
BC上的高K=0,AB上的高斜率不存在,AC边上的高K=-1
选做:已知长方形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2).求第四个顶点D的坐标.
