八年级上册数学沪教版 暑期-第02讲最简二次根式与同类二次根式 讲义(无答案)
文档属性
| 名称 | 八年级上册数学沪教版 暑期-第02讲最简二次根式与同类二次根式 讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 917.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 22:13:29 | ||
图片预览





文档简介
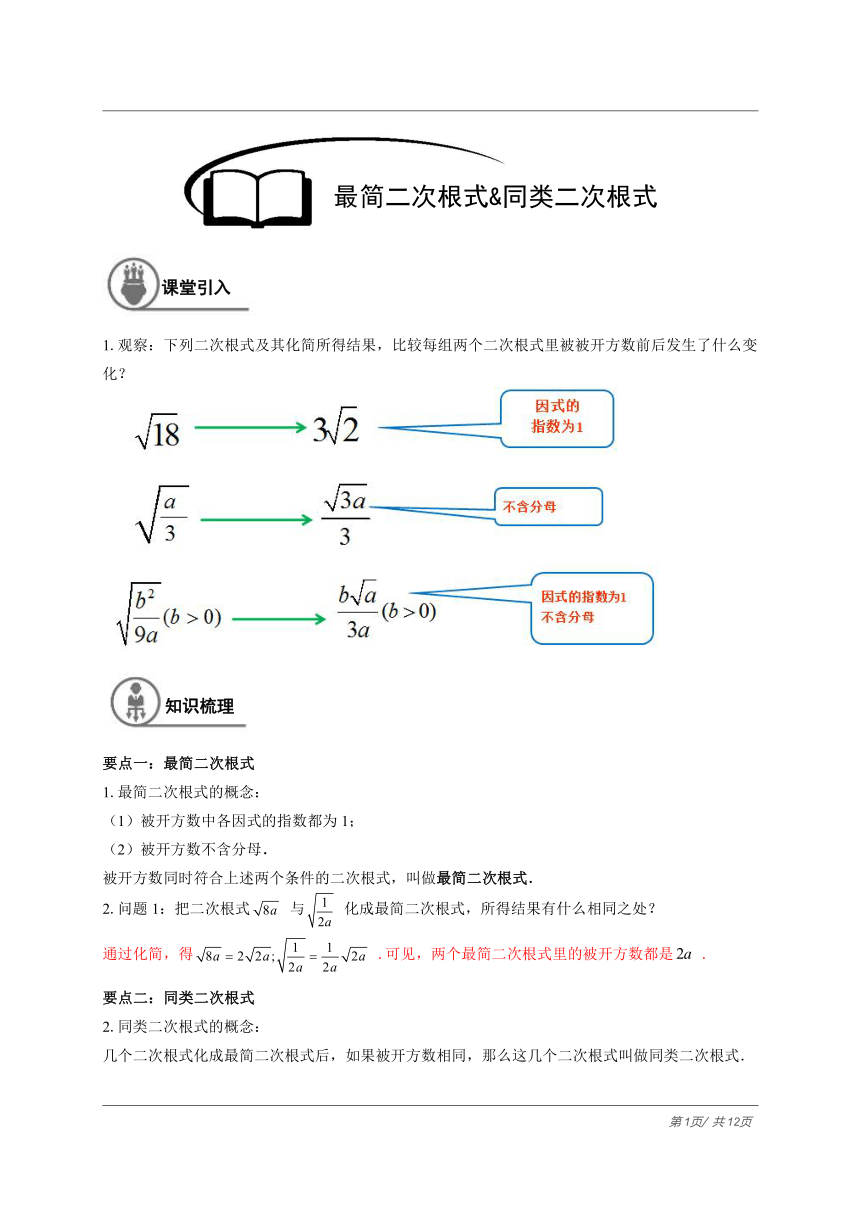
1.观察:下列二次根式及其化简所得结果,比较每组两个二次根式里被被开方数前后发生了什么变化?
要点一:最简二次根式
1.最简二次根式的概念:
(1)被开方数中各因式的指数都为1;
(2)被开方数不含分母.
被开方数同时符合上述两个条件的二次根式,叫做最简二次根式.
2.问题1:把二次根式 与 化成最简二次根式,所得结果有什么相同之处?
通过化简,得 .可见,两个最简二次根式里的被开方数都是 .
要点二:同类二次根式
2.同类二次根式的概念:
几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式.
要点一:最简二次根式
【例1】判断下列二次根式是不是最简二次根式:
(1); (2); (3); (4).
【难度】★
【例2】判断下列二次根式是不是最简二次根式:
(1); (2); (3).
【难度】★
【例3】判断下列二次根式是不是最简二次根式:
(1); (2);
(3).
【难度】★
【例4】将下列二次根式化成最简二次根式:
(1); (2); (3)(,,).
【难度】★
【例5】将下列二次根式化成最简二次根式:
(1)(); (2); (3).
【难度】★★
【例6】将下列二次根式化成最简二次根式:
(1); (2);
(3)() (4)(,,).
【难度】★★
【例7】将下列二次根式化成最简二次根式:
(1); (2); (3).
【难度】★★
【例8】如果是最简二次根式,求的值.
【难度】★★
要点二:同类二次根式
【例9】判断下列各组的二次根式是否为同类二次根式?
(1)和; (2)和.
【难度】★
【例10】判断下列各组的二次根式是否为同类二次根式?
(1),,; (2),,.
【难度】★
【例11】判断下列各组的二次根式是否为同类二次根式?
(1)和; (2)和.
【难度】★★
【例12】若最简二次根式与是同类二次根式,求、的值.
【难度】★★
【例13】若最简二次根式和是同类二次根式,求的值?
【难度】★★
【例14】合并下列各式中的同类二次根式:
(1); (2);
(3); (4).
【难度】★
【例15】合并下列各式中的同类二次根式并计算.
(1); (2);
(3); (4).
【难度】★★
【例16】合并下列各式中的同类二次根式:
(1); (2);
(3).
【难度】★★
【例17】计算:
(1); (2).
【难度】★★
1.被开方数中的因式是指因式分解和素因数分解后的因式和因数.
2.如果一个二次根式不是最简二次根式,那么可以利用化简二次根式的方法,把它化成最简二次根式.
3.在多项式中,遇到同类项就可以合并.
【巩固1】判断下列二次根式是不是最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固2】下列式子中是最简二次根式的是:
(1); (2); (3).
【难度】★
【巩固3】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固4】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固5】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固6】下列二次根式,哪些是同类二次根式:
①,②,③,④,⑤,⑥.
【难度】★
【巩固7】下列各组二次根式,是否是同类二次根式.
(1),,;(2),,;(3),,.
【难度】★
【巩固8】判断下列各组根式是否是同类根式:
(1),,;
(2)当时,,,.
【难度】★★
【巩固9】合并下列二次根式中的同类二次根式:
(1); (2);
(3); (4).
【难度】★
【巩固10】已知最简二次根式和是同类根式,求的值.
【难度】★★
【巩固11】若,则化简得( )
A.; B.; C.; D..
【难度】★★
【巩固12】将下列二次根式化成最简二次根式.
(1); (2);
(3); (4).
【难度】★★
【巩固13】将下列二次根式化成最简二次根式.
(1); (2);
(3); (4).
【难度】★★
【巩固14】将下列二次根式化成最简二次根式:
(1); (2);
(3).
【难度】★★
【巩固15】合并下列各式中的同类二次根式.
(1); (2);
(3);(4).
【难度】★★
【巩固16】已知最简二次根式与是同类二次根式,求的值.
【难度】★★
【例1】将下列式子化成最简二次根式:
(1); (2).
【难度】★★★
【例2】将下列式子化成最简二次根式:
(1); (2); (3).
【难度】★★★
【例3】若与是同类二次根式,求的最小正整数?
【难度】★★★
【例4】把化成最简二次根式.
【难度】★★★
【例5】合并下列各式中的同类二次根式:
(1);
(2);
(3).
【难度】★★★
【巩固1】把下列二次根式化简:
(1); (2).
【难度】★★★
【巩固2】观察下列各式,你能得出怎样的结论?并给出证明.
,
,
……
【难度】★★★
【巩固3】合并下列各式中的同类二次根式:
(1); (2);
(3); (4)().
【难度】★★★
第1页/ 共11页
要点一:最简二次根式
1.最简二次根式的概念:
(1)被开方数中各因式的指数都为1;
(2)被开方数不含分母.
被开方数同时符合上述两个条件的二次根式,叫做最简二次根式.
2.问题1:把二次根式 与 化成最简二次根式,所得结果有什么相同之处?
通过化简,得 .可见,两个最简二次根式里的被开方数都是 .
要点二:同类二次根式
2.同类二次根式的概念:
几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式.
要点一:最简二次根式
【例1】判断下列二次根式是不是最简二次根式:
(1); (2); (3); (4).
【难度】★
【例2】判断下列二次根式是不是最简二次根式:
(1); (2); (3).
【难度】★
【例3】判断下列二次根式是不是最简二次根式:
(1); (2);
(3).
【难度】★
【例4】将下列二次根式化成最简二次根式:
(1); (2); (3)(,,).
【难度】★
【例5】将下列二次根式化成最简二次根式:
(1)(); (2); (3).
【难度】★★
【例6】将下列二次根式化成最简二次根式:
(1); (2);
(3)() (4)(,,).
【难度】★★
【例7】将下列二次根式化成最简二次根式:
(1); (2); (3).
【难度】★★
【例8】如果是最简二次根式,求的值.
【难度】★★
要点二:同类二次根式
【例9】判断下列各组的二次根式是否为同类二次根式?
(1)和; (2)和.
【难度】★
【例10】判断下列各组的二次根式是否为同类二次根式?
(1),,; (2),,.
【难度】★
【例11】判断下列各组的二次根式是否为同类二次根式?
(1)和; (2)和.
【难度】★★
【例12】若最简二次根式与是同类二次根式,求、的值.
【难度】★★
【例13】若最简二次根式和是同类二次根式,求的值?
【难度】★★
【例14】合并下列各式中的同类二次根式:
(1); (2);
(3); (4).
【难度】★
【例15】合并下列各式中的同类二次根式并计算.
(1); (2);
(3); (4).
【难度】★★
【例16】合并下列各式中的同类二次根式:
(1); (2);
(3).
【难度】★★
【例17】计算:
(1); (2).
【难度】★★
1.被开方数中的因式是指因式分解和素因数分解后的因式和因数.
2.如果一个二次根式不是最简二次根式,那么可以利用化简二次根式的方法,把它化成最简二次根式.
3.在多项式中,遇到同类项就可以合并.
【巩固1】判断下列二次根式是不是最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固2】下列式子中是最简二次根式的是:
(1); (2); (3).
【难度】★
【巩固3】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固4】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固5】将下列二次根式化成最简二次根式:
(1); (2); (3); (4).
【难度】★
【巩固6】下列二次根式,哪些是同类二次根式:
①,②,③,④,⑤,⑥.
【难度】★
【巩固7】下列各组二次根式,是否是同类二次根式.
(1),,;(2),,;(3),,.
【难度】★
【巩固8】判断下列各组根式是否是同类根式:
(1),,;
(2)当时,,,.
【难度】★★
【巩固9】合并下列二次根式中的同类二次根式:
(1); (2);
(3); (4).
【难度】★
【巩固10】已知最简二次根式和是同类根式,求的值.
【难度】★★
【巩固11】若,则化简得( )
A.; B.; C.; D..
【难度】★★
【巩固12】将下列二次根式化成最简二次根式.
(1); (2);
(3); (4).
【难度】★★
【巩固13】将下列二次根式化成最简二次根式.
(1); (2);
(3); (4).
【难度】★★
【巩固14】将下列二次根式化成最简二次根式:
(1); (2);
(3).
【难度】★★
【巩固15】合并下列各式中的同类二次根式.
(1); (2);
(3);(4).
【难度】★★
【巩固16】已知最简二次根式与是同类二次根式,求的值.
【难度】★★
【例1】将下列式子化成最简二次根式:
(1); (2).
【难度】★★★
【例2】将下列式子化成最简二次根式:
(1); (2); (3).
【难度】★★★
【例3】若与是同类二次根式,求的最小正整数?
【难度】★★★
【例4】把化成最简二次根式.
【难度】★★★
【例5】合并下列各式中的同类二次根式:
(1);
(2);
(3).
【难度】★★★
【巩固1】把下列二次根式化简:
(1); (2).
【难度】★★★
【巩固2】观察下列各式,你能得出怎样的结论?并给出证明.
,
,
……
【难度】★★★
【巩固3】合并下列各式中的同类二次根式:
(1); (2);
(3); (4)().
【难度】★★★
第1页/ 共11页
