第11章 几何证明初步检测题(附答案)
文档属性
| 名称 | 第11章 几何证明初步检测题(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-15 00:00:00 | ||
图片预览

文档简介
第11章几何证明初步检测题
一、选择题(每题4分,共48分)
1、在下列命题中不属于公理的是( )
A、两点之间,线段最短 B、两点确定一条直线
C、三角形的三个内角的和等于1800
D、两直线平行,同位角相等
2、下列命题中的假命题是( )。
A、如果一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等,那么两个直角三角形全等
B、等腰三角形顶角的平分线把它分成两个全等的三角形
C、周长相等的两个三角形全等
D、有一条直角边对应相等的两个等腰直角三角形全等
3、下列命题中,逆命题是假命题的是( )
A、等腰三角形的两底角相等
B、等边三角形三个角都是60°
C、等腰三角形是轴对称图形
D、垂直于同一条直线的两直线平行
4、下列语句中属于定义的是( )
A、直角都相等 B、作已知角的平分线
C、连结两点的线段的长度,叫做这两点间的距离
D、两点之间,线段最短
5、下列语句属于命题的是( )
A、画一个角等于已知角 B、a>b吗?
C、延长射线OA D、对顶角相等
6、如图,如果∠B=∠D=∠AEF,那么( )。
A、AB∥CD B、BC∥AD C、BC∥EF D、AD∥EF.
7、如图是张华在纸片上任意画出来的一个五角星,试求它的五个内角的度数和为( )
A、900 B、1800 C、1200 D、3600
8、若一个三角形三个内角的度数的比为2:7:4,那么这个三角形是( )
A、钝角三角形 B、锐角三角形 C、直角三角形 D、等边三角形
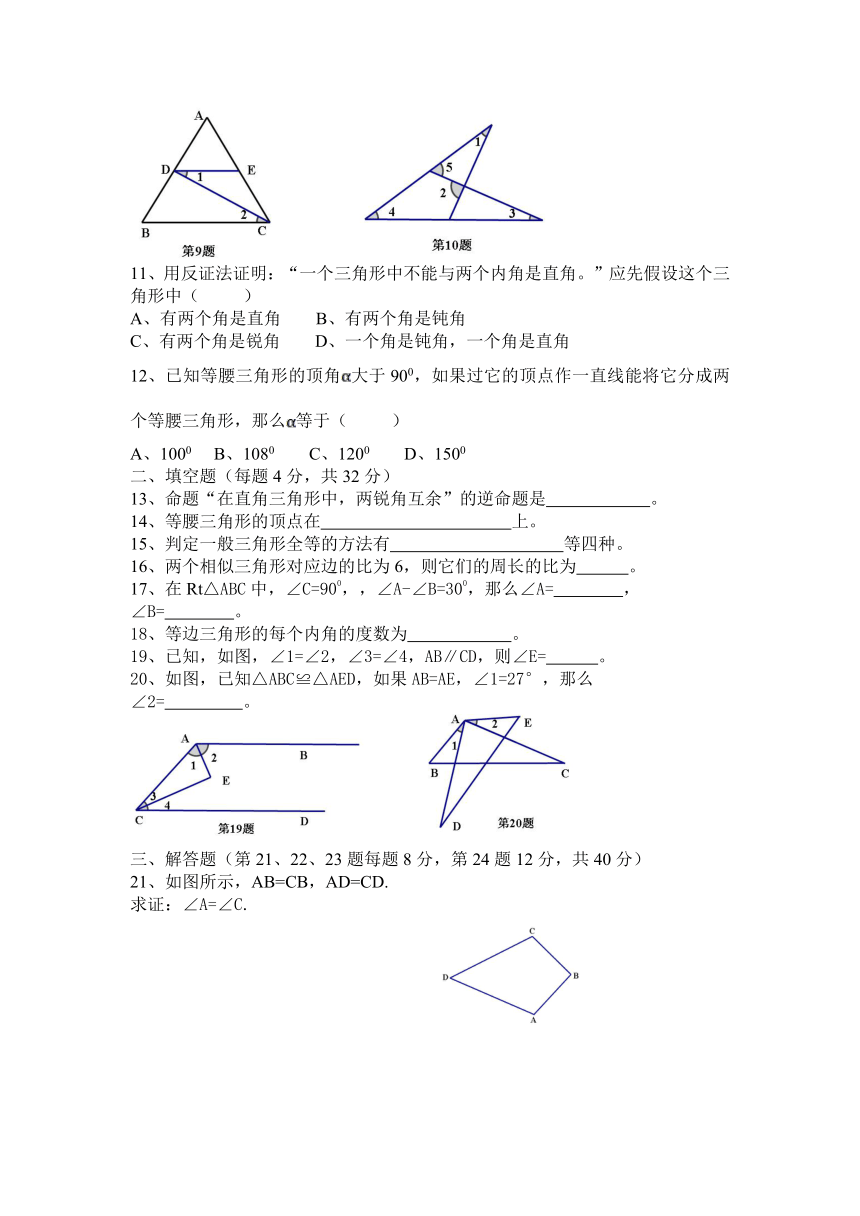
9、如图,“∵∠1=∠2,∴DE∥BC,”这步推理的依据是( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行
C、同位角相等,两直线平行 D、两直线平行,同旁内角相等
10、如图,∠1,∠2,∠3,∠4之间的数量关系总满足( )
A、∠1+∠2=∠3+∠4 B、∠1+∠2=∠4-∠3
C、∠1+∠4=∠3+∠2 D、∠1+∠4=∠2-∠3
11、用反证法证明:“一个三角形中不能与两个内角是直角。”应先假设这个三角形中( )
A、有两个角是直角 B、有两个角是钝角
C、有两个角是锐角 D、一个角是钝角,一个角是直角
12、已知等腰三角形的顶角大于900,如果过它的顶点作一直线能将它分成两个等腰三角形,那么等于( )
A、1000 B、1080 C、1200 D、1500
二、填空题(每题4分,共32分)
13、命题“在直角三角形中,两锐角互余”的逆命题是 。
14、等腰三角形的顶点在 上。
15、判定一般三角形全等的方法有 等四种。
16、两个相似三角形对应边的比为6,则它们的周长的比为 。
17、在Rt△ABC中,∠C=900,,∠A-∠B=300,那么∠A= ,
∠B= 。
18、等边三角形的每个内角的度数为 。
19、已知,如图,∠1=∠2,∠3=∠4,AB∥CD,则∠E= 。
20、如图,已知△ABC≌△AED,如果AB=AE,∠1=27°,那么
∠2= 。
三、解答题(第21、22、23题每题8分,第24题12分,共40分)
21、如图所示,AB=CB,AD=CD.
求证:∠A=∠C.
22、如图所示,D是∠AOB的平分线OC上一点,DE⊥OA于点E,DF⊥OB于点F.
求证:∠DEF=∠DFE.
23、等腰三角形的底角等于150,腰长为2a,求等腰三角形的面积。
24、如图所示,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE.
(2)求∠DFC的度数.
答案:
一、选择题1、C 2、C 3、C 4、C 5、D 6、C 7、D 8、A
9、B 10、D 11、A 12、B
二、填空题
13、两锐角互余的三角形是直角三角形
14、在底边的垂直平分线上
15、ASA,SAS,SSS,AAS。
16、6 17、600、300 18、600 19、900 20、270
三、解答题
21、略22、略23、a2 24、(1)略(2)600
一、选择题(每题4分,共48分)
1、在下列命题中不属于公理的是( )
A、两点之间,线段最短 B、两点确定一条直线
C、三角形的三个内角的和等于1800
D、两直线平行,同位角相等
2、下列命题中的假命题是( )。
A、如果一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等,那么两个直角三角形全等
B、等腰三角形顶角的平分线把它分成两个全等的三角形
C、周长相等的两个三角形全等
D、有一条直角边对应相等的两个等腰直角三角形全等
3、下列命题中,逆命题是假命题的是( )
A、等腰三角形的两底角相等
B、等边三角形三个角都是60°
C、等腰三角形是轴对称图形
D、垂直于同一条直线的两直线平行
4、下列语句中属于定义的是( )
A、直角都相等 B、作已知角的平分线
C、连结两点的线段的长度,叫做这两点间的距离
D、两点之间,线段最短
5、下列语句属于命题的是( )
A、画一个角等于已知角 B、a>b吗?
C、延长射线OA D、对顶角相等
6、如图,如果∠B=∠D=∠AEF,那么( )。
A、AB∥CD B、BC∥AD C、BC∥EF D、AD∥EF.
7、如图是张华在纸片上任意画出来的一个五角星,试求它的五个内角的度数和为( )
A、900 B、1800 C、1200 D、3600
8、若一个三角形三个内角的度数的比为2:7:4,那么这个三角形是( )
A、钝角三角形 B、锐角三角形 C、直角三角形 D、等边三角形
9、如图,“∵∠1=∠2,∴DE∥BC,”这步推理的依据是( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行
C、同位角相等,两直线平行 D、两直线平行,同旁内角相等
10、如图,∠1,∠2,∠3,∠4之间的数量关系总满足( )
A、∠1+∠2=∠3+∠4 B、∠1+∠2=∠4-∠3
C、∠1+∠4=∠3+∠2 D、∠1+∠4=∠2-∠3
11、用反证法证明:“一个三角形中不能与两个内角是直角。”应先假设这个三角形中( )
A、有两个角是直角 B、有两个角是钝角
C、有两个角是锐角 D、一个角是钝角,一个角是直角
12、已知等腰三角形的顶角大于900,如果过它的顶点作一直线能将它分成两个等腰三角形,那么等于( )
A、1000 B、1080 C、1200 D、1500
二、填空题(每题4分,共32分)
13、命题“在直角三角形中,两锐角互余”的逆命题是 。
14、等腰三角形的顶点在 上。
15、判定一般三角形全等的方法有 等四种。
16、两个相似三角形对应边的比为6,则它们的周长的比为 。
17、在Rt△ABC中,∠C=900,,∠A-∠B=300,那么∠A= ,
∠B= 。
18、等边三角形的每个内角的度数为 。
19、已知,如图,∠1=∠2,∠3=∠4,AB∥CD,则∠E= 。
20、如图,已知△ABC≌△AED,如果AB=AE,∠1=27°,那么
∠2= 。
三、解答题(第21、22、23题每题8分,第24题12分,共40分)
21、如图所示,AB=CB,AD=CD.
求证:∠A=∠C.
22、如图所示,D是∠AOB的平分线OC上一点,DE⊥OA于点E,DF⊥OB于点F.
求证:∠DEF=∠DFE.
23、等腰三角形的底角等于150,腰长为2a,求等腰三角形的面积。
24、如图所示,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE.
(2)求∠DFC的度数.
答案:
一、选择题1、C 2、C 3、C 4、C 5、D 6、C 7、D 8、A
9、B 10、D 11、A 12、B
二、填空题
13、两锐角互余的三角形是直角三角形
14、在底边的垂直平分线上
15、ASA,SAS,SSS,AAS。
16、6 17、600、300 18、600 19、900 20、270
三、解答题
21、略22、略23、a2 24、(1)略(2)600
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
