数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 864.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 21:15:02 | ||
图片预览





文档简介
(共17张PPT)
3.1.1 椭圆及其标准方程
一、学习目标:(1分钟)
1.掌握椭圆的定义;
2.掌握椭圆的标准方程.
二、问题导学:(14分钟)
1、椭圆定义是如何定义的?有什么限制条件?
2、椭圆的标准方程怎么样?有什么特点?
阅读课本P105-107内容,思考下列问题:
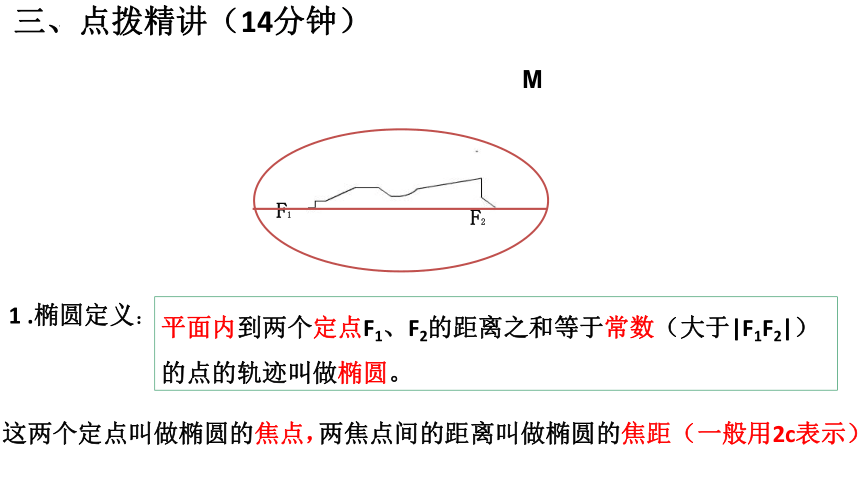
三、点拨精讲(14分钟)
F1
F2
M
1 .椭圆定义:
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,
两焦点间的距离叫做椭圆的焦距(一般用2c表示)
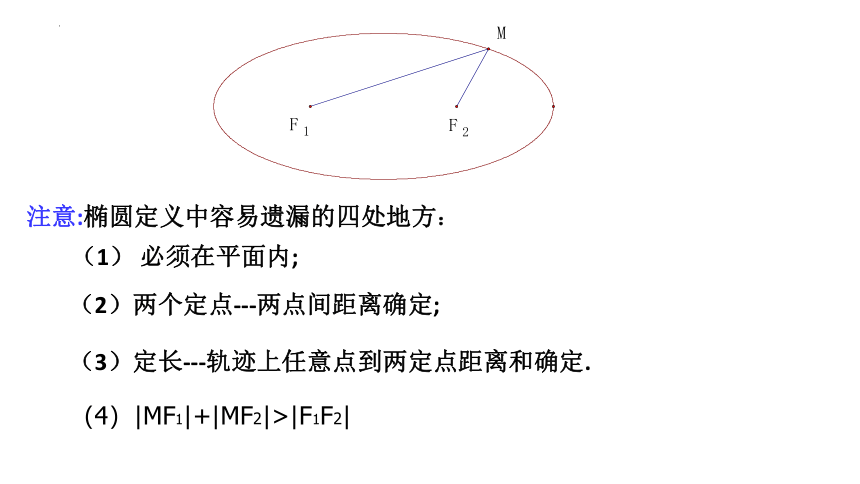
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
(4)|MF1|+|MF2|>|F1F2|
M
F
2
F
1
思考:
感悟:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(1)已知A(-3,0),B(3,0),M点到A,B两点的距离和为10,则M点的轨迹是什么
(2)已知A(-3,0),B(3,0),M点到A,B两点的距离和为6,则M点的轨迹是什么
(3)已知A(-3,0),B(3,0),M点到A,B两点的距离和为5,则M点的轨迹是什么
椭圆
线段AB
不存在
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
F1
F2
M
基本步骤:
(1)建系
(2)设点
(3)限式
(4)代换
(5)化简、证明
求轨迹方程的流程---------建设现代化
2、求椭圆的方程:
如何建立适当平面直角坐标系?
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
O
x
y
x
F1
F2
M
0
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c),则F1、F2的坐标分别 是( c,0)、(c,0) .
由椭圆的定义得:
代入坐标
(问题:下面怎样化简?)
由椭圆定义可知
两边再平方,得
移项,再平方
椭圆的标准方程
椭圆的标准方程⑴
F1
F2
M
0
x
y
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
椭圆的标准方程⑵
x
M
F1
F2
y
O
(2)焦点在y轴上:
(1) 焦点在x轴上:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
(-c,0)
( c, 0)
(0 ,c)
(0 , -c)
焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
看 , 项的分母大小,哪个分母大,焦点就在哪个坐标轴上
(3) a ,b ,c间的关系:
大小不确定
(1)方程的特点:
(2)判断焦点在哪轴上的方法
答:在 x 轴。(-3,0)和(3,0)
答:在 y 轴。(0,-5)和(0,5)
答:在y 轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则: 焦点在分母大的那个轴上。
判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标:
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
椭圆定义:
1、椭圆定义:
椭圆的标准方程
2、椭圆的标准方程:
一个定义
两个方程
四、课堂小结:(1分钟)
1、填空:已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________,
5
4
3
(3,0)、(-3,0)
6
20
若椭圆的方程为 呢?
五、当堂检测:(15分钟)
2.椭圆的两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点M到两焦点距离之和等于10,求椭圆的标准方程。
3.方程 表示焦点在y轴上的椭圆,则实数m的取值范围是 .
04.椭圆 上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|=( )
A. 2 B. 4 C. 8 D.1.5
B
5.已知椭圆满足 a+b=10, ,求此椭圆标准方程.
3.1.1 椭圆及其标准方程
一、学习目标:(1分钟)
1.掌握椭圆的定义;
2.掌握椭圆的标准方程.
二、问题导学:(14分钟)
1、椭圆定义是如何定义的?有什么限制条件?
2、椭圆的标准方程怎么样?有什么特点?
阅读课本P105-107内容,思考下列问题:
三、点拨精讲(14分钟)
F1
F2
M
1 .椭圆定义:
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,
两焦点间的距离叫做椭圆的焦距(一般用2c表示)
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
(4)|MF1|+|MF2|>|F1F2|
M
F
2
F
1
思考:
感悟:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(1)已知A(-3,0),B(3,0),M点到A,B两点的距离和为10,则M点的轨迹是什么
(2)已知A(-3,0),B(3,0),M点到A,B两点的距离和为6,则M点的轨迹是什么
(3)已知A(-3,0),B(3,0),M点到A,B两点的距离和为5,则M点的轨迹是什么
椭圆
线段AB
不存在
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
F1
F2
M
基本步骤:
(1)建系
(2)设点
(3)限式
(4)代换
(5)化简、证明
求轨迹方程的流程---------建设现代化
2、求椭圆的方程:
如何建立适当平面直角坐标系?
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
O
x
y
x
F1
F2
M
0
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c),则F1、F2的坐标分别 是( c,0)、(c,0) .
由椭圆的定义得:
代入坐标
(问题:下面怎样化简?)
由椭圆定义可知
两边再平方,得
移项,再平方
椭圆的标准方程
椭圆的标准方程⑴
F1
F2
M
0
x
y
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
椭圆的标准方程⑵
x
M
F1
F2
y
O
(2)焦点在y轴上:
(1) 焦点在x轴上:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
(-c,0)
( c, 0)
(0 ,c)
(0 , -c)
焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
看 , 项的分母大小,哪个分母大,焦点就在哪个坐标轴上
(3) a ,b ,c间的关系:
大小不确定
(1)方程的特点:
(2)判断焦点在哪轴上的方法
答:在 x 轴。(-3,0)和(3,0)
答:在 y 轴。(0,-5)和(0,5)
答:在y 轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则: 焦点在分母大的那个轴上。
判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标:
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
椭圆定义:
1、椭圆定义:
椭圆的标准方程
2、椭圆的标准方程:
一个定义
两个方程
四、课堂小结:(1分钟)
1、填空:已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________,
5
4
3
(3,0)、(-3,0)
6
20
若椭圆的方程为 呢?
五、当堂检测:(15分钟)
2.椭圆的两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点M到两焦点距离之和等于10,求椭圆的标准方程。
3.方程 表示焦点在y轴上的椭圆,则实数m的取值范围是 .
0
A. 2 B. 4 C. 8 D.1.5
B
5.已知椭圆满足 a+b=10, ,求此椭圆标准方程.
