人教A版(2019)必修第一册3.1.1函数的概念 课件(共18张ppt)
文档属性
| 名称 | 人教A版(2019)必修第一册3.1.1函数的概念 课件(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 515.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-03 21:21:06 | ||
图片预览






文档简介
(共18张PPT)
函数的概念
知识点回顾
初中阶段我们都学过哪些函数呢?
一次函数:
y=kx+b(k,b为常数,k≠0)
二次函数:
y=ax +bx+c(a,b,c为常数,a≠0)
反比例函数:
y=k/x(k为常数且k≠0)
复习回顾
初中学习的函数的定义是什么?
设在一个变化过程中有两个变量x和y,
如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量.
一枚炮弹发射后,经过26s落到地面
击中目标. 炮弹的射高为845m, 且炮弹距
地面的高度h(单位:m)随时间 t (单位: s )
变化的规律是h=130t-5t2.
实例一
创 设 情 境
A中的任意一个时间t,按照对应关系h=130t-5t2,在数集B中都有唯一确定的高度h和它对应
h=130t-5t2
南极臭氧层空洞的面积
0
5
10
15
25
20
30
26
S/106km2
t/年
1979
81
83
85
87
89
91
93
95
97
99
2001
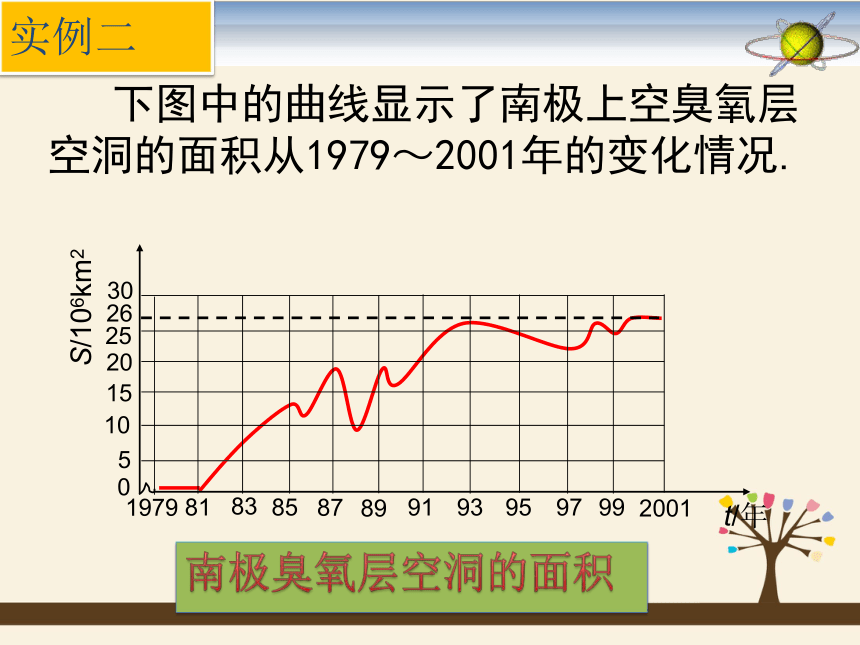
下图中的曲线显示了南极上空臭氧层
空洞的面积从1979~2001年的变化情况.
实例二
A中的任意一个时间t,按照图中曲线,在数集B中都有唯一确定的面积S和它对应
南极臭氧层空洞的面积
0
5
10
15
25
20
30
26
S/106km2
t/年
1979
81
83
85
87
89
91
93
95
97
99
2001
“八五”计划以来我国城镇居民
恩格尔系数变化情况
1992
52.9
1993
1999
1998
1997
1996
1995
1994
2000
50.1
49.9
48.6
49.9
46.4
44.5
41.9
39.2
1991
2001
53.8
37.9
时 间
(年)
恩格尔
系数(%)
仿照实例(1)(2),试描述上表中恩格尔系数和时间(年)的关系.
A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}
B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}
实例三
A中的任意一个时间t,按照表格,
在数集B中都有唯一确定的系数和它对应
A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}
B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}
探究新知
实例一,实例二,实例三的对应关系在呈现方式上有什么不同?
实例一是用解析式表示对应关系,实例二是用图像表示对应关系,实例三是用表格表示对应关系.
以上三个实例有什么共同点?
(2)两个数集间都有一种确定的对应关系;
(3)对于数集A中的任意一个数,数集B中
都有唯一确定的数和它对应.
(1)都有两个非空数集A,B;
满足以上共同点的两个数集的对应关系我们把它叫做什么呢?
归纳概括
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集f(x)|x∈A}叫做函数的值域.
1. A,B是非空的数集
函数的定义
设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作:y= f(x) ,x∈A.
注意
3.确定的对应关系,对应关系可以是解析式,图像,表格
2.任意性和唯一性
思考:“确定的的对应关系 f”是什么意思?
f可以看作是对“x”施加的某种运算或法则
例如: ,f 就是对自变量x求平方。
思考:如何理解“ ”?
符号y=f(x)表示“ y是变量x的函数”,它仅仅是函数符号,并不表示y等于f与x的乘积。不同函数中的f表示的含义不一样
思考:
当a为常数时,f(a)表示的是自变量x=a时对应的函数值,是一个常数
思考:在从集合A到集合B的一个函数f:A→B中,
集合A是函数的定义域,集合B是函数的值域吗?
例如:
定义域为{0,1,2},值域为{0, 2,4}
例 下列可作为函数y= f (x)的图象的( )
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
D
1.本节课探讨了用集合与对应的语言描述函数的概念,并引入了函数符y=f(x).
2.突出了函数概念的本质:两个非空数集间的一种确定的对应关系.
课堂总结
作业
一、举出生活中函数的例子(两个以上),并用集合与对应的语言来描述函数.
函数的概念
知识点回顾
初中阶段我们都学过哪些函数呢?
一次函数:
y=kx+b(k,b为常数,k≠0)
二次函数:
y=ax +bx+c(a,b,c为常数,a≠0)
反比例函数:
y=k/x(k为常数且k≠0)
复习回顾
初中学习的函数的定义是什么?
设在一个变化过程中有两个变量x和y,
如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量.
一枚炮弹发射后,经过26s落到地面
击中目标. 炮弹的射高为845m, 且炮弹距
地面的高度h(单位:m)随时间 t (单位: s )
变化的规律是h=130t-5t2.
实例一
创 设 情 境
A中的任意一个时间t,按照对应关系h=130t-5t2,在数集B中都有唯一确定的高度h和它对应
h=130t-5t2
南极臭氧层空洞的面积
0
5
10
15
25
20
30
26
S/106km2
t/年
1979
81
83
85
87
89
91
93
95
97
99
2001
下图中的曲线显示了南极上空臭氧层
空洞的面积从1979~2001年的变化情况.
实例二
A中的任意一个时间t,按照图中曲线,在数集B中都有唯一确定的面积S和它对应
南极臭氧层空洞的面积
0
5
10
15
25
20
30
26
S/106km2
t/年
1979
81
83
85
87
89
91
93
95
97
99
2001
“八五”计划以来我国城镇居民
恩格尔系数变化情况
1992
52.9
1993
1999
1998
1997
1996
1995
1994
2000
50.1
49.9
48.6
49.9
46.4
44.5
41.9
39.2
1991
2001
53.8
37.9
时 间
(年)
恩格尔
系数(%)
仿照实例(1)(2),试描述上表中恩格尔系数和时间(年)的关系.
A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}
B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}
实例三
A中的任意一个时间t,按照表格,
在数集B中都有唯一确定的系数和它对应
A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}
B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}
探究新知
实例一,实例二,实例三的对应关系在呈现方式上有什么不同?
实例一是用解析式表示对应关系,实例二是用图像表示对应关系,实例三是用表格表示对应关系.
以上三个实例有什么共同点?
(2)两个数集间都有一种确定的对应关系;
(3)对于数集A中的任意一个数,数集B中
都有唯一确定的数和它对应.
(1)都有两个非空数集A,B;
满足以上共同点的两个数集的对应关系我们把它叫做什么呢?
归纳概括
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集f(x)|x∈A}叫做函数的值域.
1. A,B是非空的数集
函数的定义
设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作:y= f(x) ,x∈A.
注意
3.确定的对应关系,对应关系可以是解析式,图像,表格
2.任意性和唯一性
思考:“确定的的对应关系 f”是什么意思?
f可以看作是对“x”施加的某种运算或法则
例如: ,f 就是对自变量x求平方。
思考:如何理解“ ”?
符号y=f(x)表示“ y是变量x的函数”,它仅仅是函数符号,并不表示y等于f与x的乘积。不同函数中的f表示的含义不一样
思考:
当a为常数时,f(a)表示的是自变量x=a时对应的函数值,是一个常数
思考:在从集合A到集合B的一个函数f:A→B中,
集合A是函数的定义域,集合B是函数的值域吗?
例如:
定义域为{0,1,2},值域为{0, 2,4}
例 下列可作为函数y= f (x)的图象的( )
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
D
1.本节课探讨了用集合与对应的语言描述函数的概念,并引入了函数符y=f(x).
2.突出了函数概念的本质:两个非空数集间的一种确定的对应关系.
课堂总结
作业
一、举出生活中函数的例子(两个以上),并用集合与对应的语言来描述函数.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
