20.1 平行四边形的判定(共4课时)
文档属性
| 名称 | 20.1 平行四边形的判定(共4课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-16 15:52:23 | ||
图片预览










文档简介
课件62张PPT。华东师大
八年级(下)
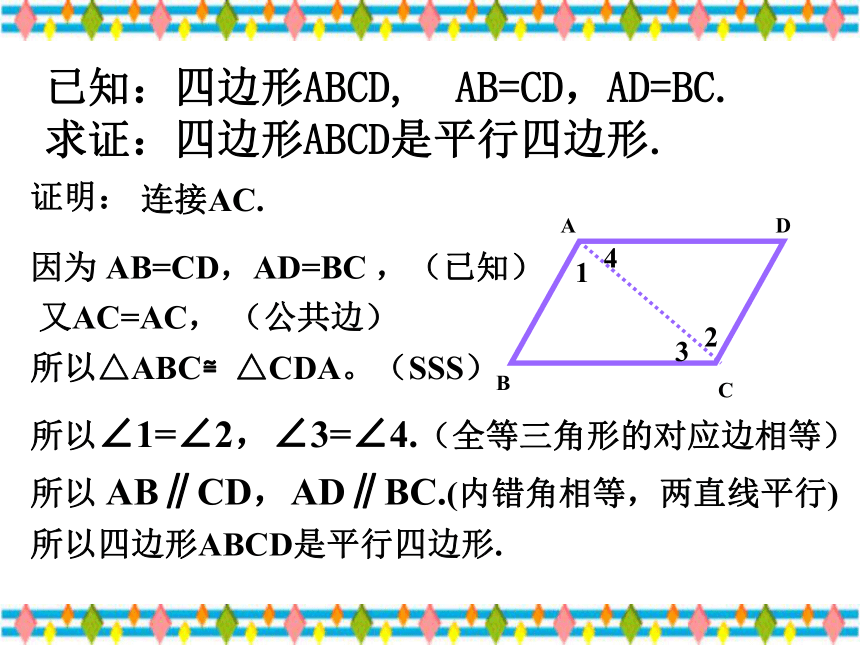
数 学 课 件华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第1课时)想一想有两组对边平行的四边形是平行四边形.2.平行四边形的对边相等;平行四边形的性质:3.平行四边形的对角相等;4.平行四边形的对角线互相平分.平行四边形的定义:1. 平行四边形的两组对边分别平行;试一试1.两组对边分别相等的四边形是平行四边形猜想:BDAC已知:四边形ABCD, AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.2134连接AC.证明:所以∠1=∠2,∠3=∠4.(全等三角形的对应边相等)
所以 AB∥CD,AD∥BC.(内错角相等,两直线平行)
所以四边形ABCD是平行四边形.因为 AB=CD,AD=BC ,(已知)
又AC=AC, (公共边)
所以△ABC≌△CDA。(SSS)两组对边分别相等的四边形
是平行四边形平行四边形判定定理1:比一比 平行四边形的两组对边相等;平行四边形性质定理1:平行四边形判定定理1: 两组对边分别相等的四边形
是平行四边形平行四边形的判定:定义:有两组对边平行的四边形是平行四边形。平行四边形的性质:定义:平行四边形的两组对边分别平行。比一比性质:判定:1.平行四边形的对边
平行;
2.平行四边形的对边
相等;
3.平行四边形的一组对边平行且相等。1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
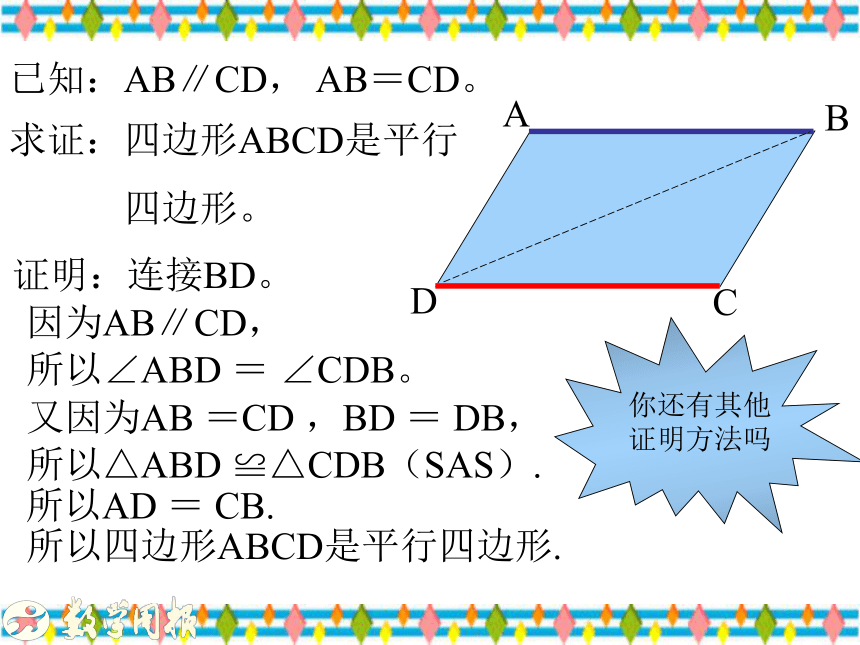
3.一组对边平行且相等的四边形是平行四边形。猜测:比一比猜想数学命题:一组对边平行且相等的四边形是平行四边形.试一试已知:AB∥CD, AB=CD。求证:四边形ABCD是平行
四边形。证明:连接BD。因为AB∥CD,所以∠ABD = ∠CDB。又因为AB =CD ,BD = DB,所以△ABD ≌△CDB(SAS).所以AD = CB.所以四边形ABCD是平行四边形.判定定理2: 一组对边平行且相等的四边形是平行四边形。1、请你识别下列四边形哪些是平行四边形?做一做 做一做 2. 如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。 一组对边平行且相等的四边形是平行四边形。3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战做一做 小结
1.本节课你学会了几种平行四边形的判定方法。2.本节课所学的解决问题的思路是什么?华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第2课时)知识回顾判定一个四边形是平行四边形已学过哪些方法?定义:两组对边分别平行的四边形叫平行四边形。定理1:一组对边平行并且相等的四边形是平行四边形。定理2:两组对边分别相等的四边形是平行四边形。如图,在 中,P1、P2是对角线BD的三等分点。求证:四边形AP1CP2是平行四边形。练习平行四边形判定定理: 1. 两组对边分别平行的四边形是平行四边形。因为AB∥CD,AD∥BC(已知),
所以四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)。 数学语言表示为: 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙根据上节课的讲解,我们知道如果AB=CD,AD=BC,则四边形ABCD是平行四边形;或是AB∥CD,或AB=CD,则四边形ABCD也是平行四边形。 2. 两组对边分别相等的四边形是平行四边形。因为AB=CD,AD=BC(已知),
所以四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)。 数学语言表示为: 3. 一组对边平行且相等的四边形是平行四边形。因为AB=CD,AB∥CD(已知),
所以四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。 数学语言表示为: 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
从小丽的做法中,你能得出
怎样的结论?O猜想:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中所以△AOB≌△COD(SAS)。所以AB=CD。同理 AD=CB。所以四 边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)。
平行四边形判定定理 :4. 对角线互相平分的四边形是平行四边形。因为A0=C0,B0=D0(已知),
所以四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。数学语言表示为:O猜想:两组对角分别相等的四边形是平行四边形已知:在四边形ABCD中,∠ A= ∠C,∠B= ∠D,
求证:四边形ABCD是平行四边形。证明:因为∠A=∠C,∠B=∠D,
又∠A+ ∠B+ ∠C+ ∠D =360 °,
所以 2∠A+ 2∠B=360 °,
即∠A+ ∠B=180 °.
所以 AD∥BC 。同理,可证AB∥CD。
所以四边形ABCD是平行四边形。试一试其他的方法平行四边形判定定理 :5. 两组对角分别相等的四边形是平行四边形。因为∠A=∠C,∠B=∠D (已知),
所以四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)。数学语言表示为:1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、一组对边平行且相等的四边形是平行四边形。 5、两组对角分别相等的四边形是平行四边形例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连接BD,交AC于点O。因为四边形ABCD是平行四边形,所以AO=CO,BO=DO。因为AE=CF, 所以EO=FO。因为BO=DO,所以四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.小试牛刀 如图, AB=CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗?你有几种判别方法?已知:平行四边形ABCD的对角线AC、BD相交于点O,M、N、P、Q分别OA、OB、OC、OD的中点。求证四边形MNPQ是平行四边形。证明:因为ABCD是平行四边形,所以OA=OC,OD = OB.因为M、N、P、Q 分别OA、OB、OC、OD的中点,所以OM=OP,OQ = ON。所以四边形MNPQ是平行四边形。拓展训练已知:如图,在 中,E,F是对角线BD上的两点,∠BAE=∠DCF.
求证:四边形AECF是平行四边形。例2O课内练习1.如图:在 中,E,F是对角线AC上的两个点;G,H是对角线B,D上的两点.已知AE=CF,DG=BH,求证:四边形EHFG是平行四边形.OHGFEDCBA探究活动 任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现。发现:三角形一条边上的中线的2倍小于另两条边的和。E已知:如图,AD是⊿ABC的中线,求证:2ADAE,所以AB+AC>2AD,即2AD1、平行四边形对边
2、平行四边形对角
3、平行四边形对角线平行相等互相平分相等4、平行四边形是中心对称图形1、两组对边分别平行的四边形是平行四边形。2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、一组对边平行且相等的四边形是平行四边形。 5、两组对角分别相等的四边形是平行四边形☆判定方法:创新训练:(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)一组对边相等,一组对角相等的四边形是平行四边形吗? 使同学们明白假命题应举反例说明。
三道练习一方面求同,另一方面求异,提高素质能力。(3)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。一组对边相等,一组对角相等的四边形是平行四边形吗?有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗? 不一定。如右图练习1:如图, AB = CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗? 思 考 练习2:如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试说明四边形AFCE是平行四边形。CBDAFE练习3:如图在 ABCD中,E、F、G、H分别是各边上 的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。1、在四边形ABCD中,从(1)AB∥ CD,(2)BC ∥ AD (3)AB=CD(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A 3种 B 4种 C 5种 D 6种
2、不能判定四边形ABCD是平行四边形的条件是( )
A .AB=CD AD=BC B .AB∥CD AB=CD
C.AB=CD AD∥BC C.AB∥CD AD∥ BC
华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第4课时)平行四边形 平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形两组对边分别平行四边形四边形平行四边形平行四边形的性质定理:平行四边形的对边相等.′因为四边形ABCD是平行四边形,
所以AB=CD,BC=DA.定理:平行四边形的对角相等.因为四边形ABCD是平行四边形,
所以∠A=∠C, ∠B=∠D.定理:平行四边形的对角线互相平分.因为四边形ABCD是平行四边形,
所以CO=AO,BO=DO.推论:夹在两条平行线间的平行
线段相等.因为MN∥PQ,AB∥CD,
所以AB=CD.1.下列性质中,平行四边形不一定具备的
是( )(A)对角相等 (B)邻角互补
(C )对角互补 (D)内角和是360°C2.如图,在平行四边形ABCD中,
∠1 = ∠B =50°,则∠2 = 。80°ABCDO(1)50°30cm2(a+b)AD平行四边形的判定′定理:两组对边分别相等的四边形是平行四边形. 定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.定理:两组对角分别相等的四边形是平行四边形.因为AB=CD,AD=BC,
所以四边形ABCD是平行四边形.因为AB∥CD,AB=CD,
所以四边形ABCD是平行四边形.因为AO=CO,BO=DO,
所以四边形ABCD是平行四边形.因为∠A=∠C,∠B=∠D,
所以四边形ABCD是平行四边形.例1 如图,四边形ABCD为平行四边形,延长BA至点E,延长DC至点F,使BE=DF,AF交BC于点H,CE交AD于点G。
求证:∠E=∠F。证明:因为四边形ABCD是平行四边形,BE=DF,四边形AFCE是平行四边形。注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F。所以所以所以所以又因为选择题:(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;下面判定四边形是平行四边形的方法
中,错误的是( )。(C )一组对边平行,一组对角相等;
( D)一组对边平行,另一组对边相等DF860°120°6cm, 8cm′ 2,已知:如图,在□ ABCD中,BF=DE.求证:四边形AFCE是平行四边形. 3、已知:如图,在□ ABCD中,∠ABC的平分线与AD相交于点P. 求证:PD+CD=BC.3分析:可过点P作PE∥DC交BC于点E,对问题进行转化。 4、如图,四边形ABCD与EBFD均是平行四边形.求证:AE=CF. 5、已知:如图, AC,BD是□ ABCD的两条对角线, AE⊥BD,CF⊥BD垂足分别是E,F.求证:AE=CF.6、如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且BE∥DF.
求证:∠1=∠2。 ′7、已知:如图.求证:四边形MNOP是平行四边形.分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.证明:∴四边形MNPO是平行四边形.
八年级(下)
数 学 课 件华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第1课时)想一想有两组对边平行的四边形是平行四边形.2.平行四边形的对边相等;平行四边形的性质:3.平行四边形的对角相等;4.平行四边形的对角线互相平分.平行四边形的定义:1. 平行四边形的两组对边分别平行;试一试1.两组对边分别相等的四边形是平行四边形猜想:BDAC已知:四边形ABCD, AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.2134连接AC.证明:所以∠1=∠2,∠3=∠4.(全等三角形的对应边相等)
所以 AB∥CD,AD∥BC.(内错角相等,两直线平行)
所以四边形ABCD是平行四边形.因为 AB=CD,AD=BC ,(已知)
又AC=AC, (公共边)
所以△ABC≌△CDA。(SSS)两组对边分别相等的四边形
是平行四边形平行四边形判定定理1:比一比 平行四边形的两组对边相等;平行四边形性质定理1:平行四边形判定定理1: 两组对边分别相等的四边形
是平行四边形平行四边形的判定:定义:有两组对边平行的四边形是平行四边形。平行四边形的性质:定义:平行四边形的两组对边分别平行。比一比性质:判定:1.平行四边形的对边
平行;
2.平行四边形的对边
相等;
3.平行四边形的一组对边平行且相等。1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.一组对边平行且相等的四边形是平行四边形。猜测:比一比猜想数学命题:一组对边平行且相等的四边形是平行四边形.试一试已知:AB∥CD, AB=CD。求证:四边形ABCD是平行
四边形。证明:连接BD。因为AB∥CD,所以∠ABD = ∠CDB。又因为AB =CD ,BD = DB,所以△ABD ≌△CDB(SAS).所以AD = CB.所以四边形ABCD是平行四边形.判定定理2: 一组对边平行且相等的四边形是平行四边形。1、请你识别下列四边形哪些是平行四边形?做一做 做一做 2. 如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。 一组对边平行且相等的四边形是平行四边形。3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战做一做 小结
1.本节课你学会了几种平行四边形的判定方法。2.本节课所学的解决问题的思路是什么?华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第2课时)知识回顾判定一个四边形是平行四边形已学过哪些方法?定义:两组对边分别平行的四边形叫平行四边形。定理1:一组对边平行并且相等的四边形是平行四边形。定理2:两组对边分别相等的四边形是平行四边形。如图,在 中,P1、P2是对角线BD的三等分点。求证:四边形AP1CP2是平行四边形。练习平行四边形判定定理: 1. 两组对边分别平行的四边形是平行四边形。因为AB∥CD,AD∥BC(已知),
所以四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)。 数学语言表示为: 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙根据上节课的讲解,我们知道如果AB=CD,AD=BC,则四边形ABCD是平行四边形;或是AB∥CD,或AB=CD,则四边形ABCD也是平行四边形。 2. 两组对边分别相等的四边形是平行四边形。因为AB=CD,AD=BC(已知),
所以四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)。 数学语言表示为: 3. 一组对边平行且相等的四边形是平行四边形。因为AB=CD,AB∥CD(已知),
所以四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。 数学语言表示为: 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
从小丽的做法中,你能得出
怎样的结论?O猜想:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中所以△AOB≌△COD(SAS)。所以AB=CD。同理 AD=CB。所以四 边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)。
平行四边形判定定理 :4. 对角线互相平分的四边形是平行四边形。因为A0=C0,B0=D0(已知),
所以四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。数学语言表示为:O猜想:两组对角分别相等的四边形是平行四边形已知:在四边形ABCD中,∠ A= ∠C,∠B= ∠D,
求证:四边形ABCD是平行四边形。证明:因为∠A=∠C,∠B=∠D,
又∠A+ ∠B+ ∠C+ ∠D =360 °,
所以 2∠A+ 2∠B=360 °,
即∠A+ ∠B=180 °.
所以 AD∥BC 。同理,可证AB∥CD。
所以四边形ABCD是平行四边形。试一试其他的方法平行四边形判定定理 :5. 两组对角分别相等的四边形是平行四边形。因为∠A=∠C,∠B=∠D (已知),
所以四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)。数学语言表示为:1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、一组对边平行且相等的四边形是平行四边形。 5、两组对角分别相等的四边形是平行四边形例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连接BD,交AC于点O。因为四边形ABCD是平行四边形,所以AO=CO,BO=DO。因为AE=CF, 所以EO=FO。因为BO=DO,所以四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.小试牛刀 如图, AB=CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗?你有几种判别方法?已知:平行四边形ABCD的对角线AC、BD相交于点O,M、N、P、Q分别OA、OB、OC、OD的中点。求证四边形MNPQ是平行四边形。证明:因为ABCD是平行四边形,所以OA=OC,OD = OB.因为M、N、P、Q 分别OA、OB、OC、OD的中点,所以OM=OP,OQ = ON。所以四边形MNPQ是平行四边形。拓展训练已知:如图,在 中,E,F是对角线BD上的两点,∠BAE=∠DCF.
求证:四边形AECF是平行四边形。例2O课内练习1.如图:在 中,E,F是对角线AC上的两个点;G,H是对角线B,D上的两点.已知AE=CF,DG=BH,求证:四边形EHFG是平行四边形.OHGFEDCBA探究活动 任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现。发现:三角形一条边上的中线的2倍小于另两条边的和。E已知:如图,AD是⊿ABC的中线,求证:2AD
2、平行四边形对角
3、平行四边形对角线平行相等互相平分相等4、平行四边形是中心对称图形1、两组对边分别平行的四边形是平行四边形。2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、一组对边平行且相等的四边形是平行四边形。 5、两组对角分别相等的四边形是平行四边形☆判定方法:创新训练:(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)一组对边相等,一组对角相等的四边形是平行四边形吗? 使同学们明白假命题应举反例说明。
三道练习一方面求同,另一方面求异,提高素质能力。(3)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。一组对边相等,一组对角相等的四边形是平行四边形吗?有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗? 不一定。如右图练习1:如图, AB = CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗? 思 考 练习2:如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试说明四边形AFCE是平行四边形。CBDAFE练习3:如图在 ABCD中,E、F、G、H分别是各边上 的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。1、在四边形ABCD中,从(1)AB∥ CD,(2)BC ∥ AD (3)AB=CD(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A 3种 B 4种 C 5种 D 6种
2、不能判定四边形ABCD是平行四边形的条件是( )
A .AB=CD AD=BC B .AB∥CD AB=CD
C.AB=CD AD∥BC C.AB∥CD AD∥ BC
华东师大版八年级(下册)第20章 平行四边形的判定20.1 平行四边形的判定(第4课时)平行四边形 平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形两组对边分别平行四边形四边形平行四边形平行四边形的性质定理:平行四边形的对边相等.′因为四边形ABCD是平行四边形,
所以AB=CD,BC=DA.定理:平行四边形的对角相等.因为四边形ABCD是平行四边形,
所以∠A=∠C, ∠B=∠D.定理:平行四边形的对角线互相平分.因为四边形ABCD是平行四边形,
所以CO=AO,BO=DO.推论:夹在两条平行线间的平行
线段相等.因为MN∥PQ,AB∥CD,
所以AB=CD.1.下列性质中,平行四边形不一定具备的
是( )(A)对角相等 (B)邻角互补
(C )对角互补 (D)内角和是360°C2.如图,在平行四边形ABCD中,
∠1 = ∠B =50°,则∠2 = 。80°ABCDO(1)50°30cm2(a+b)AD平行四边形的判定′定理:两组对边分别相等的四边形是平行四边形. 定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.定理:两组对角分别相等的四边形是平行四边形.因为AB=CD,AD=BC,
所以四边形ABCD是平行四边形.因为AB∥CD,AB=CD,
所以四边形ABCD是平行四边形.因为AO=CO,BO=DO,
所以四边形ABCD是平行四边形.因为∠A=∠C,∠B=∠D,
所以四边形ABCD是平行四边形.例1 如图,四边形ABCD为平行四边形,延长BA至点E,延长DC至点F,使BE=DF,AF交BC于点H,CE交AD于点G。
求证:∠E=∠F。证明:因为四边形ABCD是平行四边形,BE=DF,四边形AFCE是平行四边形。注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F。所以所以所以所以又因为选择题:(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;下面判定四边形是平行四边形的方法
中,错误的是( )。(C )一组对边平行,一组对角相等;
( D)一组对边平行,另一组对边相等DF860°120°6cm, 8cm′ 2,已知:如图,在□ ABCD中,BF=DE.求证:四边形AFCE是平行四边形. 3、已知:如图,在□ ABCD中,∠ABC的平分线与AD相交于点P. 求证:PD+CD=BC.3分析:可过点P作PE∥DC交BC于点E,对问题进行转化。 4、如图,四边形ABCD与EBFD均是平行四边形.求证:AE=CF. 5、已知:如图, AC,BD是□ ABCD的两条对角线, AE⊥BD,CF⊥BD垂足分别是E,F.求证:AE=CF.6、如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且BE∥DF.
求证:∠1=∠2。 ′7、已知:如图.求证:四边形MNOP是平行四边形.分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.证明:∴四边形MNPO是平行四边形.
