人教版数学八年级下册 18.1 平行四边形第2课时 平行四边形的性质(2) 课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形第2课时 平行四边形的性质(2) 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 384.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-04 20:28:18 | ||
图片预览




文档简介
(共29张PPT)
18.1 平行四边形
第18章 平行四边形
第2课时 平行四边形的性质(2)
18.1.1 平行四边形的性质
复习引入
1.平行四边形的定义是什么?
平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.平行四边形有何性质?
(2)平行四边形的对角相等;
(3)平行四边形的邻角互补.
(1)平行四边形的对边相等;
复习引入
3.如何证明平行四边形的这些性质?
复习引入
A
D
B
C
O
≌
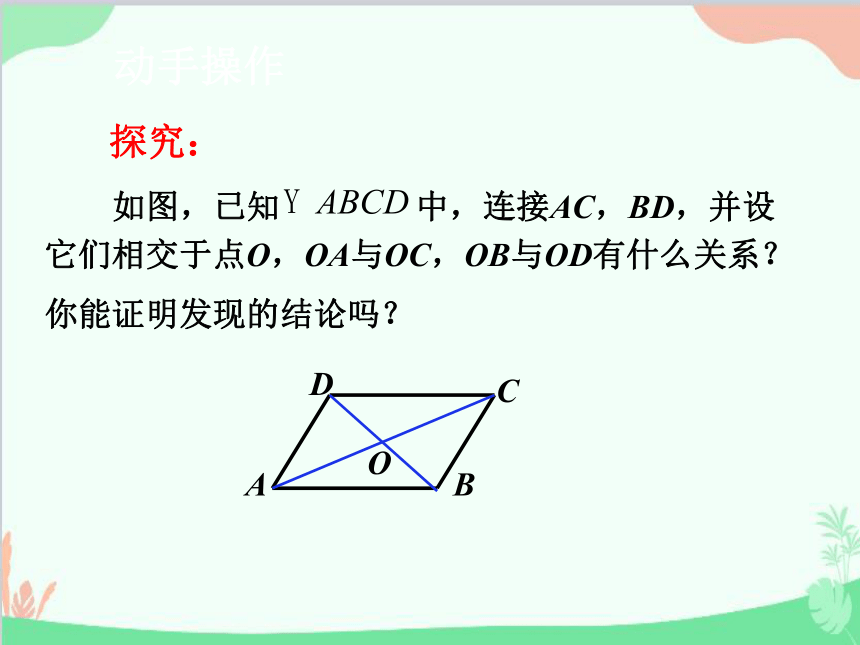
探究:
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
动手操作
A
D
B
C
O
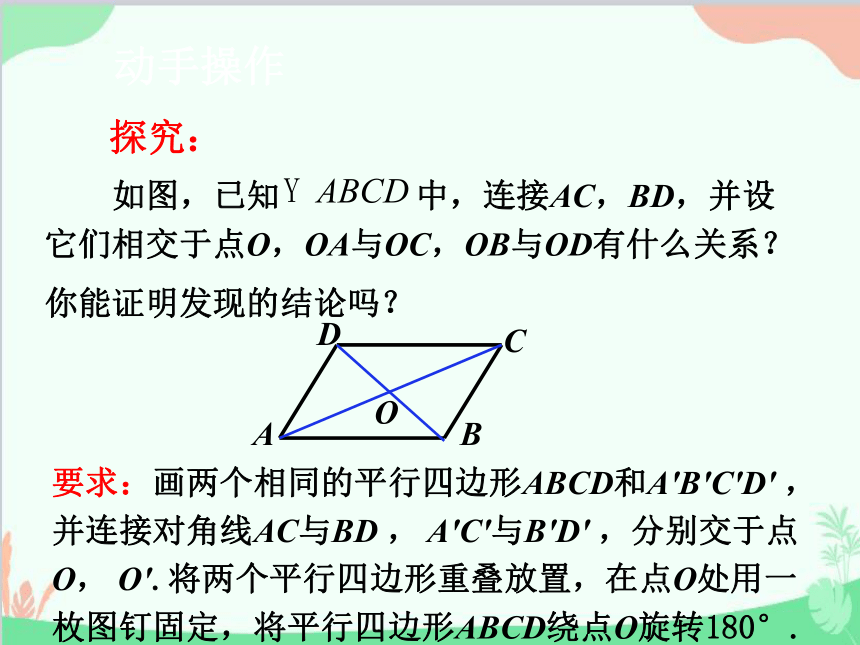
探究:
动手操作
A
D
B
C
O
要求:画两个相同的平行四边形ABCD和A'B'C'D' ,并连接对角线AC与BD , A'C'与B'D' ,分别交于点O, O'.将两个平行四边形重叠放置,在点O处用一枚图钉固定,将平行四边形ABCD绕点O旋转180°.
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
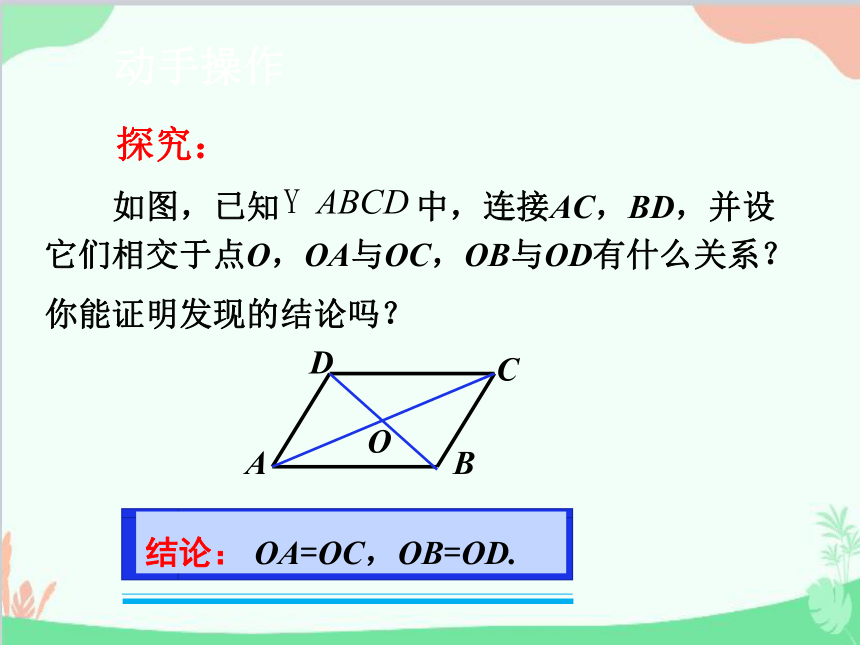
探究:
结论: OA=OC,OB=OD.
动手操作
A
D
B
C
O
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
OA=OC,OB=OD.
动手操作
A
D
B
C
O
平行四边形的性质三:平行四边形的对角线互相平分.
问题:
已知 中,AC,BD相交于O,图中有哪些三角形全等?哪些线段是相等的?请用多种方法加以验证.
动手操作
A
D
B
C
O
图中有四对三角形全等,分别是:△AOB≌△COD, △AOD≌△COB,△ABD≌△CDB,△ADC≌△CBA .
有如下线段相等:OA=OC,OB=OD,AD=BC,AB=DC,证明中用到“AAS”“ASA”.
动手操作
A
D
B
C
O
已知 中,AC,BD相交于O,图中有哪些三角形全等?哪些线段是相等的?请用多种方法加以验证.
A
D
B
C
O
例2 如图,在 中,AB=10,AD=8,AC⊥BC.求BC,CD,AC,OA的长,以及
的面积.
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC,∴△ABC是直角三角形.
根据勾股定理,AC=BC= .
又OA=OC,
范例点击 应用所学
答案:28 cm
1.已知 中,对角线AC、BD交于点O,AC
=12 cm,BD=18 cm,AD=13 cm,求△BOC的周长.
随堂练习 巩固深化
2.已知 的周长为48 cm,AB比BC长4 cm,那么这个四边形的各边长分别为多少?
答案:AB=CD=14 cm,BC=AD=10 cm.
1.平行四边形的定义既是平行四边形的一个判定方法,又是平行四边形的一个性质.
2.平行四边形的性质.
对边平行且相等
对角相等
对角线互相平分
3.对角线是解决平行四边形问题的常用辅助线.
课堂总结 发展潜能
边 角 对角线
性质
图形
1.教材44页练习第1,2题.
2.习题18.1第3题.
布置作业 专题突破
18.1 平行四边形
第18章 平行四边形
第2课时 平行四边形的性质(2)
18.1.1 平行四边形的性质
复习引入
1.平行四边形的定义是什么?
平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.平行四边形有何性质?
(2)平行四边形的对角相等;
(3)平行四边形的邻角互补.
(1)平行四边形的对边相等;
复习引入
3.如何证明平行四边形的这些性质?
复习引入
A
D
B
C
O
≌
探究:
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
动手操作
A
D
B
C
O
探究:
动手操作
A
D
B
C
O
要求:画两个相同的平行四边形ABCD和A'B'C'D' ,并连接对角线AC与BD , A'C'与B'D' ,分别交于点O, O'.将两个平行四边形重叠放置,在点O处用一枚图钉固定,将平行四边形ABCD绕点O旋转180°.
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
探究:
结论: OA=OC,OB=OD.
动手操作
A
D
B
C
O
如图,已知 中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
OA=OC,OB=OD.
动手操作
A
D
B
C
O
平行四边形的性质三:平行四边形的对角线互相平分.
问题:
已知 中,AC,BD相交于O,图中有哪些三角形全等?哪些线段是相等的?请用多种方法加以验证.
动手操作
A
D
B
C
O
图中有四对三角形全等,分别是:△AOB≌△COD, △AOD≌△COB,△ABD≌△CDB,△ADC≌△CBA .
有如下线段相等:OA=OC,OB=OD,AD=BC,AB=DC,证明中用到“AAS”“ASA”.
动手操作
A
D
B
C
O
已知 中,AC,BD相交于O,图中有哪些三角形全等?哪些线段是相等的?请用多种方法加以验证.
A
D
B
C
O
例2 如图,在 中,AB=10,AD=8,AC⊥BC.求BC,CD,AC,OA的长,以及
的面积.
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC,∴△ABC是直角三角形.
根据勾股定理,AC=BC= .
又OA=OC,
范例点击 应用所学
答案:28 cm
1.已知 中,对角线AC、BD交于点O,AC
=12 cm,BD=18 cm,AD=13 cm,求△BOC的周长.
随堂练习 巩固深化
2.已知 的周长为48 cm,AB比BC长4 cm,那么这个四边形的各边长分别为多少?
答案:AB=CD=14 cm,BC=AD=10 cm.
1.平行四边形的定义既是平行四边形的一个判定方法,又是平行四边形的一个性质.
2.平行四边形的性质.
对边平行且相等
对角相等
对角线互相平分
3.对角线是解决平行四边形问题的常用辅助线.
课堂总结 发展潜能
边 角 对角线
性质
图形
1.教材44页练习第1,2题.
2.习题18.1第3题.
布置作业 专题突破
