北师大版数学六年级下册 总复习第1课时 式与方程 课件(20张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 总复习第1课时 式与方程 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-04 10:56:11 | ||
图片预览








文档简介
(共20张PPT)
3 式与方程
第1课时 式与方程
总复习—数与代数
北师版数学六年级下册
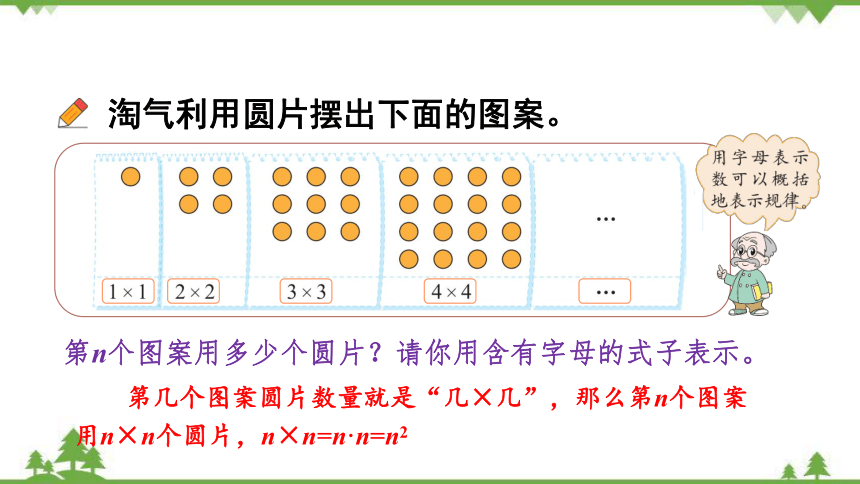
淘气利用圆片摆出下面的图案。
第n个图案用多少个圆片?请你用含有字母的式子表示。
第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2
用字母表示数、运算定律和计算公式
用字母表示数量关系:用字母或含有字母的式子可以表示数量,也可以表示数量关系、运算定律和计算公式等,为研究和解决问题带来很多方便。
如用s表示路程,v表示速度,t表示时间,那么路程、速度、时间之间的关系可表示为:s=vt
用字母表示数量关系。
总价=单价×数量
c=an
c=at
用字母表示计算公式。
正方形的周长:
C=4a
平行四边形的面积:
S=ab
正方形的面积:
S=a
梯形的面积:
S=(a+b)h÷2
圆的面积:
S=πr
圆柱的体积:
V=Sh
工作总量=工作效率×工作时间
用字母表示运算定律。
名称 用字母表示
加法交换律 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=ac+bc
用字母表示计算方法。
用字母表示除法、分数或比时,表示除数、分母以及
比的后项的字母不能是0。
用字母表示运算结果时,必须是最简明的式子。
解下面的方程,并说一说你是怎么解的。
解:
9x 1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x 1.8=5.4
解:
(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
0.8x+1.2x=25
等式
等式的意义:表示相等关系的式子叫做等式。
等式的性质:1. 等式的两边都加上(或减去)同一个
数,左右两边仍然相等。这就是等式
的性质(1)。
2. 等式的两边都乘(或除以)同一个不
为0的数,左右两边仍然相等。这就
是等式的性质(2)。
方程
方程的意义:1. 含有未知数的等式叫做方程。
2. 所有的方程都是等式,但等式却不全
是方程。
解方程:求方程的解的过程叫做解方程。解方程的依
据是等式的性质。
1. 填一填。
(1)比x少25的数是 。
(2)n的5倍与m的差是 。
(3)一件衬衫a元,一件毛衣的价格是它的2倍
还多6元,毛衣的价格是 元。
(4)原价a元的产品打八折后的价钱是 元。
x 25
5n m
2a+6
80%a
2.
两车分别从A,B两地同时出发,相向而行,经过2.5小时相遇。
(1)两地间的距离是多少?
2.5(a+b)
或
2.5a+2.5b
2.
两车分别从A,B两地同时出发,相向而行,经过2.5小时相遇。
(2)当a=45,b=60时,求两地间的距离。
2.5(a+b)=2.5×(45+60)=262.5(km)
答:两地间的距离是262.5km。
3.
r
r
r
r
r
r
r
r
左图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
C=8r
S=4r2
或
C=4a=4×2r=8r
S=a =a×a=2r×2r=4r
答:正方形周长为8r,面积为4r 。
4. 摆正方形。
4
7
10
=1+3×1
=1+3×2
=1+3×3
(1)你发现了什么规律?用含有字母的式子表示出来。
1+3n
4. 摆正方形。
4
7
10
=1+3×1
=1+3×2
=1+3×3
(2)如果摆100个正方形,需要多少根小棒?
1+3n=1+3×100=301(根)
5. 解方程。
15x=60
x+2x=12.6
40%x=4.2
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
12+x=25
2x÷5=15
4x 1.6x=36
解:x=25 12
x=13
解:2x=15×5
2x=75
x=37.5
解:2.4x=36
x=15
课后作业
3 式与方程
第1课时 式与方程
总复习—数与代数
北师版数学六年级下册
淘气利用圆片摆出下面的图案。
第n个图案用多少个圆片?请你用含有字母的式子表示。
第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2
用字母表示数、运算定律和计算公式
用字母表示数量关系:用字母或含有字母的式子可以表示数量,也可以表示数量关系、运算定律和计算公式等,为研究和解决问题带来很多方便。
如用s表示路程,v表示速度,t表示时间,那么路程、速度、时间之间的关系可表示为:s=vt
用字母表示数量关系。
总价=单价×数量
c=an
c=at
用字母表示计算公式。
正方形的周长:
C=4a
平行四边形的面积:
S=ab
正方形的面积:
S=a
梯形的面积:
S=(a+b)h÷2
圆的面积:
S=πr
圆柱的体积:
V=Sh
工作总量=工作效率×工作时间
用字母表示运算定律。
名称 用字母表示
加法交换律 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=ac+bc
用字母表示计算方法。
用字母表示除法、分数或比时,表示除数、分母以及
比的后项的字母不能是0。
用字母表示运算结果时,必须是最简明的式子。
解下面的方程,并说一说你是怎么解的。
解:
9x 1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x 1.8=5.4
解:
(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
0.8x+1.2x=25
等式
等式的意义:表示相等关系的式子叫做等式。
等式的性质:1. 等式的两边都加上(或减去)同一个
数,左右两边仍然相等。这就是等式
的性质(1)。
2. 等式的两边都乘(或除以)同一个不
为0的数,左右两边仍然相等。这就
是等式的性质(2)。
方程
方程的意义:1. 含有未知数的等式叫做方程。
2. 所有的方程都是等式,但等式却不全
是方程。
解方程:求方程的解的过程叫做解方程。解方程的依
据是等式的性质。
1. 填一填。
(1)比x少25的数是 。
(2)n的5倍与m的差是 。
(3)一件衬衫a元,一件毛衣的价格是它的2倍
还多6元,毛衣的价格是 元。
(4)原价a元的产品打八折后的价钱是 元。
x 25
5n m
2a+6
80%a
2.
两车分别从A,B两地同时出发,相向而行,经过2.5小时相遇。
(1)两地间的距离是多少?
2.5(a+b)
或
2.5a+2.5b
2.
两车分别从A,B两地同时出发,相向而行,经过2.5小时相遇。
(2)当a=45,b=60时,求两地间的距离。
2.5(a+b)=2.5×(45+60)=262.5(km)
答:两地间的距离是262.5km。
3.
r
r
r
r
r
r
r
r
左图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
C=8r
S=4r2
或
C=4a=4×2r=8r
S=a =a×a=2r×2r=4r
答:正方形周长为8r,面积为4r 。
4. 摆正方形。
4
7
10
=1+3×1
=1+3×2
=1+3×3
(1)你发现了什么规律?用含有字母的式子表示出来。
1+3n
4. 摆正方形。
4
7
10
=1+3×1
=1+3×2
=1+3×3
(2)如果摆100个正方形,需要多少根小棒?
1+3n=1+3×100=301(根)
5. 解方程。
15x=60
x+2x=12.6
40%x=4.2
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
12+x=25
2x÷5=15
4x 1.6x=36
解:x=25 12
x=13
解:2x=15×5
2x=75
x=37.5
解:2.4x=36
x=15
课后作业
