北师大版数学八年级下册 6.2 平行四边形的判定第1课时 平行四边形的判定(1) 课件(共17张)
文档属性
| 名称 | 北师大版数学八年级下册 6.2 平行四边形的判定第1课时 平行四边形的判定(1) 课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 155.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-04 21:29:30 | ||
图片预览






文档简介
(共17张PPT)
第6章 平行四边形
6.2 平行四边形的判定
第1课时 平行四边形的判定(1)
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形还有哪些性质?
复习引入
平行四边形的定义:两组对边分别平行的四边形叫平行四边形.
可以用来得到平行线及相关性质.
平行四边形的对边相等、对角相等.
定理探索
活动1:
工具:两组长度分别相等的四根笔.
动手:能否在平面内用这四根笔摆成一个平行四边形?
思考:你能说明你所摆出的四边形是平行四边形吗?
定理探索
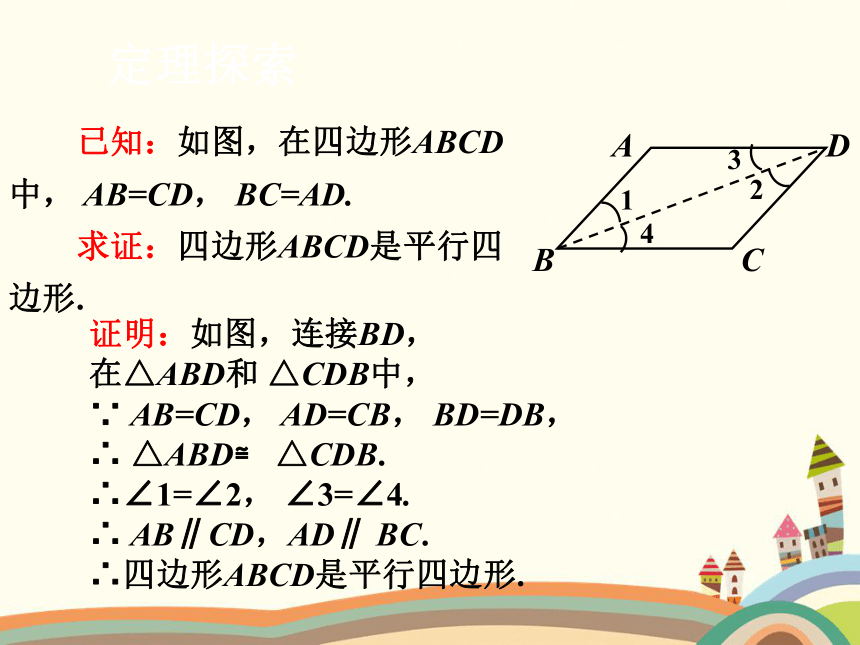
已知:如图,在四边形ABCD中, AB=CD, BC=AD.
求证:四边形ABCD是平行四边形.
证明:如图,连接BD,
在△ABD和 △CDB中,
∵ AB=CD, AD=CB, BD=DB,
∴ △ABD≌ △CDB.
∴∠1=∠2, ∠3=∠4.
∴ AB∥CD,AD∥ BC.
∴四边形ABCD是平行四边形.
B
C
D
A
1
3
2
4
定理探索
活动1:
工具:两组长度分别相等的笔.
动手:能否在平面内用这四根笔摆成一个平行四边形?
思考:以上活动事实,能用文字语言表达吗?
小组活动探究,得出:
(1)只有将两两相等的木条分别作为四边形的两组对边才能得到平行四边形.
(2)通过观察、实验、猜想到:两组对边分别相等的四边形是平行四边形.
定理探索
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
定理探索
活动2:
工具:两根长度相等的笔,两条平行线.
动手:利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
思考:你能说明你所摆出的四边形是平行四边形吗?
定理探索
已知:如图,在四边形ABCD中, AB∥CD,且AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵ AB∥CD, ∴∠BAC=∠ACD.
又∵ AB=CD, AC=CA,
∴ △BAC≌ △DCA.
∴ BC=AD.
∴四边形ABCD是平行四边形.
B
C
D
A
定理探索
活动2:
工具:两根长度相等的笔,两条平行线.
动手:利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
思考:以上活动事实,能用文字语言表达吗?
定理探索
平行四边形的判定:一组对边平行且相等的四边形是平行四边形.
例题讲解
例1.如图,在平行四边形ABCD中,E,F分别是AD,BC的中点.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC.
又∵ E,F分别是AD,BC的中点,
∴ ED= AD,BF= BC.
∴ ED=BF.
又∵ ED ∥ BF,
∴四边形BFDE是平行四边形.
B
C
D
A
E
F
随堂练习
1.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD.四边形ABCD是平行四边形吗?为什么?
解:四边形ABCD是平行四边形.
∵线段AD是线段BC经过平移得到的,
∴AD=CB, AD∥BC.
∴四边形ABCD是平行四边形.
B
C
D
A
随堂练习
2.如图所示, AC=BD=16, AB=CD=EF=15,CE=DF=9,图中有哪些互相平行的线段?
AB∥CD∥EF, AC∥BD, CE∥DF
B
D
C
A
F
E
随堂练习
3.如图所示,四个全等的三角形拼成一个大的三角形,找出图中所有的平行四边形,并说明理由.
平行四边形ABDC,
平行四边形BCDE,
平行四边形BCFD.
B
C
D
A
F
E
这节课的学习主要围绕下列几个问题:
(1)判定一个四边形是平行四边形的方法有哪几种?这些方法是从什么角度去考虑的?
(2)我们是通过什么方法得出平行四边形这几种判定方法的,这样的探索过程对你有什么启发?
(3)类比、观察、拼图、实验等都是学习数学、发现结论的常用方法.
回顾小结
1.教材习题6.3第1,2,3 题.
2.思考题:有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?为什么?
布置作业
谢谢大家!
再见!
第6章 平行四边形
6.2 平行四边形的判定
第1课时 平行四边形的判定(1)
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形还有哪些性质?
复习引入
平行四边形的定义:两组对边分别平行的四边形叫平行四边形.
可以用来得到平行线及相关性质.
平行四边形的对边相等、对角相等.
定理探索
活动1:
工具:两组长度分别相等的四根笔.
动手:能否在平面内用这四根笔摆成一个平行四边形?
思考:你能说明你所摆出的四边形是平行四边形吗?
定理探索
已知:如图,在四边形ABCD中, AB=CD, BC=AD.
求证:四边形ABCD是平行四边形.
证明:如图,连接BD,
在△ABD和 △CDB中,
∵ AB=CD, AD=CB, BD=DB,
∴ △ABD≌ △CDB.
∴∠1=∠2, ∠3=∠4.
∴ AB∥CD,AD∥ BC.
∴四边形ABCD是平行四边形.
B
C
D
A
1
3
2
4
定理探索
活动1:
工具:两组长度分别相等的笔.
动手:能否在平面内用这四根笔摆成一个平行四边形?
思考:以上活动事实,能用文字语言表达吗?
小组活动探究,得出:
(1)只有将两两相等的木条分别作为四边形的两组对边才能得到平行四边形.
(2)通过观察、实验、猜想到:两组对边分别相等的四边形是平行四边形.
定理探索
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
定理探索
活动2:
工具:两根长度相等的笔,两条平行线.
动手:利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
思考:你能说明你所摆出的四边形是平行四边形吗?
定理探索
已知:如图,在四边形ABCD中, AB∥CD,且AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵ AB∥CD, ∴∠BAC=∠ACD.
又∵ AB=CD, AC=CA,
∴ △BAC≌ △DCA.
∴ BC=AD.
∴四边形ABCD是平行四边形.
B
C
D
A
定理探索
活动2:
工具:两根长度相等的笔,两条平行线.
动手:利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
思考:以上活动事实,能用文字语言表达吗?
定理探索
平行四边形的判定:一组对边平行且相等的四边形是平行四边形.
例题讲解
例1.如图,在平行四边形ABCD中,E,F分别是AD,BC的中点.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC.
又∵ E,F分别是AD,BC的中点,
∴ ED= AD,BF= BC.
∴ ED=BF.
又∵ ED ∥ BF,
∴四边形BFDE是平行四边形.
B
C
D
A
E
F
随堂练习
1.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD.四边形ABCD是平行四边形吗?为什么?
解:四边形ABCD是平行四边形.
∵线段AD是线段BC经过平移得到的,
∴AD=CB, AD∥BC.
∴四边形ABCD是平行四边形.
B
C
D
A
随堂练习
2.如图所示, AC=BD=16, AB=CD=EF=15,CE=DF=9,图中有哪些互相平行的线段?
AB∥CD∥EF, AC∥BD, CE∥DF
B
D
C
A
F
E
随堂练习
3.如图所示,四个全等的三角形拼成一个大的三角形,找出图中所有的平行四边形,并说明理由.
平行四边形ABDC,
平行四边形BCDE,
平行四边形BCFD.
B
C
D
A
F
E
这节课的学习主要围绕下列几个问题:
(1)判定一个四边形是平行四边形的方法有哪几种?这些方法是从什么角度去考虑的?
(2)我们是通过什么方法得出平行四边形这几种判定方法的,这样的探索过程对你有什么启发?
(3)类比、观察、拼图、实验等都是学习数学、发现结论的常用方法.
回顾小结
1.教材习题6.3第1,2,3 题.
2.思考题:有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?为什么?
布置作业
谢谢大家!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
