9.2多边形的内角和与外角和学案
图片预览
文档简介
9.2 多边形的内角和与外角和
学习目标
1.了解多边形及多边形的内角、外角等概念。
2.通过不同方法探索多边形的内角和与外角和公式,并会利用它们进行有关计算。
学习重点、难点
1.重点:多边形的内角和与外角和定理。
2.难点:多边形的内角和,外角和定理的推导。
学习过程
一、学前准备
1.什么叫三角形?
2.三角形的内角和是多少?
3.什么叫三角形的外角?什么叫外角和?三角形的外角和是多少?
二、探究活动
(一)独立思考,解决问题
1.多边形的概念,
我们知道:不在同一直线上的三条线段首尾顺次连结组成的平面图形叫三角形。
你能说出什么叫四边形、五边形吗?
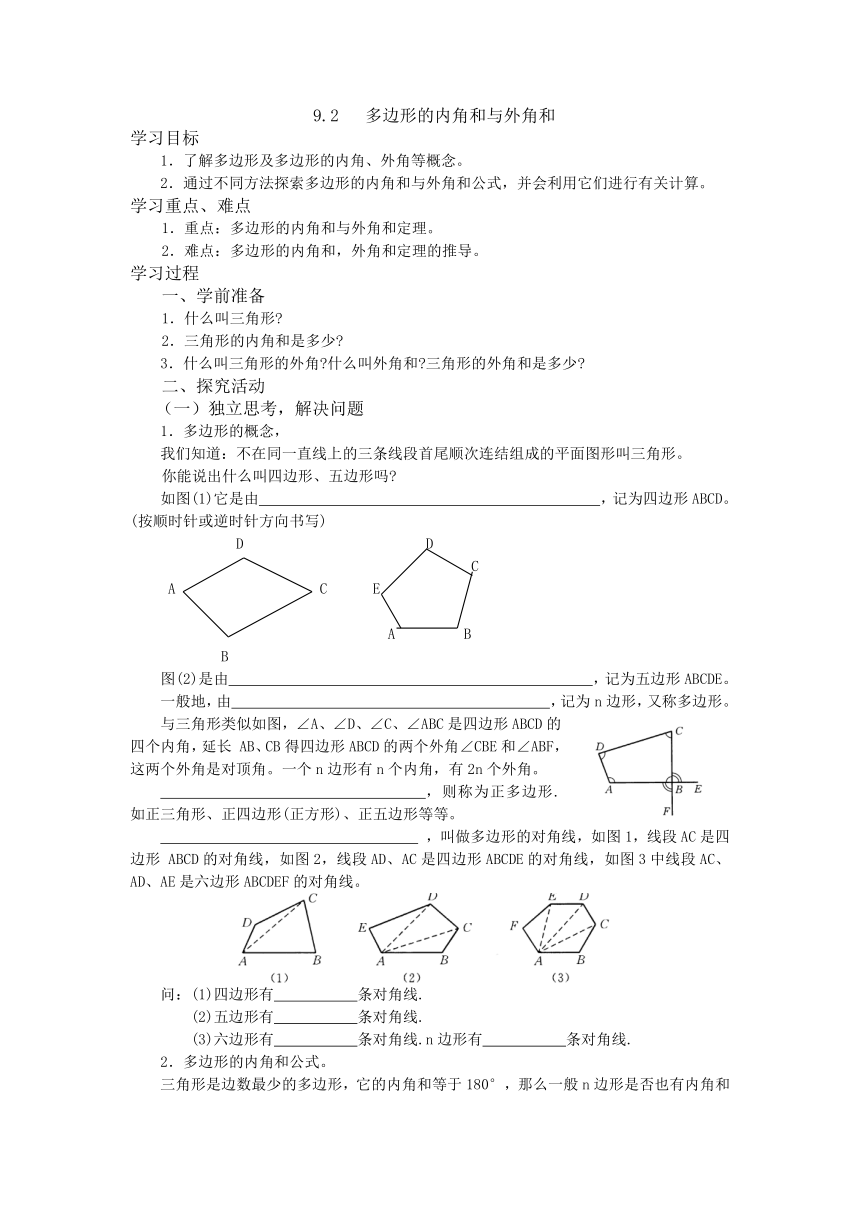
如图(1)它是由 ,记为四边形ABCD。(按顺时针或逆时针方向书写)
D D
C
A C E
A B
B
图(2)是由 ,记为五边形ABCDE。
一般地,由 ,记为n边形,又称多边形。
与三角形类似如图,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,延长 AB、CB得四边形ABCD的两个外角∠CBE和∠ABF,这两个外角是对顶角。一个n边形有n个内角,有2n个外角。
,则称为正多边形.如正三角形、正四边形(正方形)、正五边形等等。
,叫做多边形的对角线,如图1,线段AC是四边形 ABCD的对角线,如图2,线段AD、AC是四边形ABCDE的对角线,如图3中线段AC、AD、AE是六边形ABCDEF的对角线。
问:(1)四边形有 条对角线.
(2)五边形有 条对角线.
(3)六边形有 条对角线.n边形有 条对角线.
2.多边形的内角和公式。
三角形是边数最少的多边形,它的内角和等于180°,那么一般n边形是否也有内角和公式呢?让我们先从四边形,正边形,六边形……开始。
从上面对角线的研究可知,一条对角线把四边形分成 个三角形,这 个三角形的内角和就是四边形的内角和,五边形的内角和就是图中 个三角形内角和的和。
让学生填写教科书表8.3.1由此,你可以得到n边形的内角和公式是 .
3.多边形的外角和。
与三角形的外角和一样,与多边形的每个内角相邻的外角有两个,这两个角是对顶角,
称为多边形的外角和,如教科书图9.2.6,∠1+∠2+∠3+∠4就是四边形的外角和。
多边形的外角和是否也可以用公式表示呢?下面我们也来探讨。
因为n边形的一个内角与它的相邻的外角互为补角,所以可先求出多边形的内角与外角的总和,再减去内角和,就可得到外角和。
让学生填写填教科写表9.2.2
n边形的内角与外角的总和为
n边形的内角和为
那么n边形的外角和为 - =
这就是说多边形的外角和与边数 ,都等于 。
(二)精讲例题:
例1.一个多边形的内角和等于2340°,求它的边数。
例2.一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数。
三、学习体会
1、本节课你有哪些收获?你还有哪些疑惑?
2、你认为老师上课过程中还有哪些需要注意或改进的地方?
3、预习时的疑难解决了吗?
四、自我测验
1.如图五边形ABCDE中从A画对角线可画______条,由此把五边形分成_____个三角形,请在图中画出.
2.在四边形ABCD中,∠A=90°,∠C=60°,则∠B+∠D=_______度.
3.正五边形内角和为______度,每个内角为______,每个外角为_____
4.(2005,北京)如果正多边形有一个外角为72°,那么它的边数是_____.
5.在多边形中,n边形的内角和为__ __,而n边形的外角和是指在n边形的n个顶点处各取一个外角相加,其总和为__ ___,与___ ____的多少无关.
6.(2005,广州市)一个多边形的内角和与其外角和的度数总和为1260°,则这个多边形的边数为________.
7.一个五边形的三个内角是直角,另两个内角相等,则相等的这两个角是( )
A.45° B.135° C.120° D.108°
8.一个多边形的每一个外角都等于45°,则这个多边形的内角和为( )
A.720° B.675° C.1080° D.905°
9.若一个多边形的外角和与它的内角和相等,则这个多边形是( )边形.
A.三 B.四 C.五 D.六
10.若n边形的内角和与外角和之比为9:2,则该多边形为_______边形.
11.一个多边形的内角和等于1800°,则它的边数是______,共有对角线____条.
12.一个四边形的内角中,钝角最多有( )
A.一个 B.两个 C.三个 D.四个
13.一个多边形的外角不可能都等于( )
A.30° B.40° C.50° D.60°
课堂小结
本节课我们通过把多边形划分成若干个三角形,用三角形内角和去求多边形的内角和,从而得到多边形的内角和公式为(n-2)·180°。这种化未知为已知的转化方法,必须在学习中逐步掌握。由于多边形的外角和等于360°,与边数无关,所以常把多边形内角的问题转化为外角和来处理。
当堂训练
教科书P71习题9.2第1、2、3、4题。
学习目标
1.了解多边形及多边形的内角、外角等概念。
2.通过不同方法探索多边形的内角和与外角和公式,并会利用它们进行有关计算。
学习重点、难点
1.重点:多边形的内角和与外角和定理。
2.难点:多边形的内角和,外角和定理的推导。
学习过程
一、学前准备
1.什么叫三角形?
2.三角形的内角和是多少?
3.什么叫三角形的外角?什么叫外角和?三角形的外角和是多少?
二、探究活动
(一)独立思考,解决问题
1.多边形的概念,
我们知道:不在同一直线上的三条线段首尾顺次连结组成的平面图形叫三角形。
你能说出什么叫四边形、五边形吗?
如图(1)它是由 ,记为四边形ABCD。(按顺时针或逆时针方向书写)
D D
C
A C E
A B
B
图(2)是由 ,记为五边形ABCDE。
一般地,由 ,记为n边形,又称多边形。
与三角形类似如图,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,延长 AB、CB得四边形ABCD的两个外角∠CBE和∠ABF,这两个外角是对顶角。一个n边形有n个内角,有2n个外角。
,则称为正多边形.如正三角形、正四边形(正方形)、正五边形等等。
,叫做多边形的对角线,如图1,线段AC是四边形 ABCD的对角线,如图2,线段AD、AC是四边形ABCDE的对角线,如图3中线段AC、AD、AE是六边形ABCDEF的对角线。
问:(1)四边形有 条对角线.
(2)五边形有 条对角线.
(3)六边形有 条对角线.n边形有 条对角线.
2.多边形的内角和公式。
三角形是边数最少的多边形,它的内角和等于180°,那么一般n边形是否也有内角和公式呢?让我们先从四边形,正边形,六边形……开始。
从上面对角线的研究可知,一条对角线把四边形分成 个三角形,这 个三角形的内角和就是四边形的内角和,五边形的内角和就是图中 个三角形内角和的和。
让学生填写教科书表8.3.1由此,你可以得到n边形的内角和公式是 .
3.多边形的外角和。
与三角形的外角和一样,与多边形的每个内角相邻的外角有两个,这两个角是对顶角,
称为多边形的外角和,如教科书图9.2.6,∠1+∠2+∠3+∠4就是四边形的外角和。
多边形的外角和是否也可以用公式表示呢?下面我们也来探讨。
因为n边形的一个内角与它的相邻的外角互为补角,所以可先求出多边形的内角与外角的总和,再减去内角和,就可得到外角和。
让学生填写填教科写表9.2.2
n边形的内角与外角的总和为
n边形的内角和为
那么n边形的外角和为 - =
这就是说多边形的外角和与边数 ,都等于 。
(二)精讲例题:
例1.一个多边形的内角和等于2340°,求它的边数。
例2.一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数。
三、学习体会
1、本节课你有哪些收获?你还有哪些疑惑?
2、你认为老师上课过程中还有哪些需要注意或改进的地方?
3、预习时的疑难解决了吗?
四、自我测验
1.如图五边形ABCDE中从A画对角线可画______条,由此把五边形分成_____个三角形,请在图中画出.
2.在四边形ABCD中,∠A=90°,∠C=60°,则∠B+∠D=_______度.
3.正五边形内角和为______度,每个内角为______,每个外角为_____
4.(2005,北京)如果正多边形有一个外角为72°,那么它的边数是_____.
5.在多边形中,n边形的内角和为__ __,而n边形的外角和是指在n边形的n个顶点处各取一个外角相加,其总和为__ ___,与___ ____的多少无关.
6.(2005,广州市)一个多边形的内角和与其外角和的度数总和为1260°,则这个多边形的边数为________.
7.一个五边形的三个内角是直角,另两个内角相等,则相等的这两个角是( )
A.45° B.135° C.120° D.108°
8.一个多边形的每一个外角都等于45°,则这个多边形的内角和为( )
A.720° B.675° C.1080° D.905°
9.若一个多边形的外角和与它的内角和相等,则这个多边形是( )边形.
A.三 B.四 C.五 D.六
10.若n边形的内角和与外角和之比为9:2,则该多边形为_______边形.
11.一个多边形的内角和等于1800°,则它的边数是______,共有对角线____条.
12.一个四边形的内角中,钝角最多有( )
A.一个 B.两个 C.三个 D.四个
13.一个多边形的外角不可能都等于( )
A.30° B.40° C.50° D.60°
课堂小结
本节课我们通过把多边形划分成若干个三角形,用三角形内角和去求多边形的内角和,从而得到多边形的内角和公式为(n-2)·180°。这种化未知为已知的转化方法,必须在学习中逐步掌握。由于多边形的外角和等于360°,与边数无关,所以常把多边形内角的问题转化为外角和来处理。
当堂训练
教科书P71习题9.2第1、2、3、4题。
