第9章 解直角三角形复习

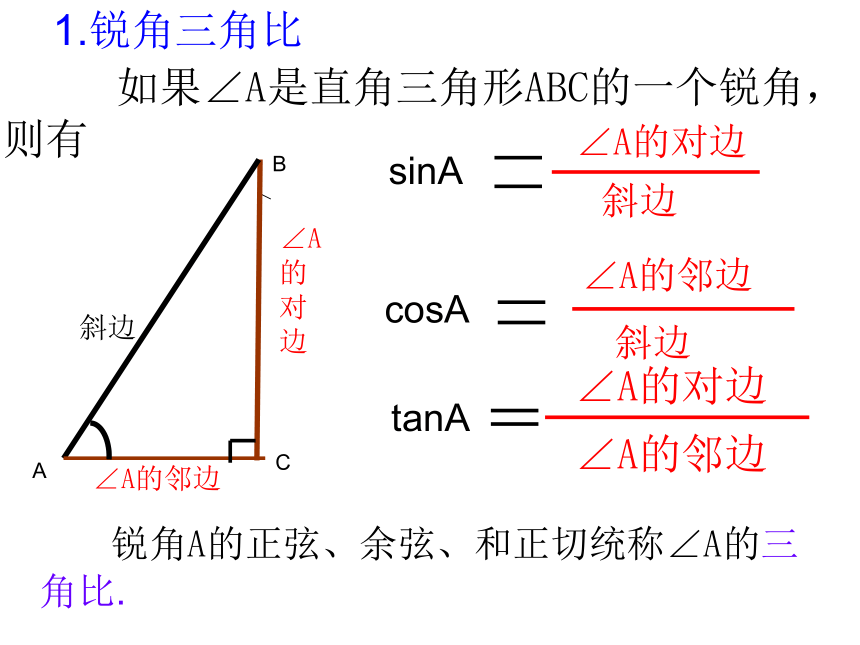
课件18张PPT。解直角三角形 如果∠A是直角三角形ABC的一个锐角，则有∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边 锐角A的正弦、余弦、和正切统称∠A的三角比.1.锐角三角比 2.在Rt△ABC中:
∠A的正弦sinA=
∠A的余弦cosA=
∠A 的正切tanA=
ACBbcaabbc
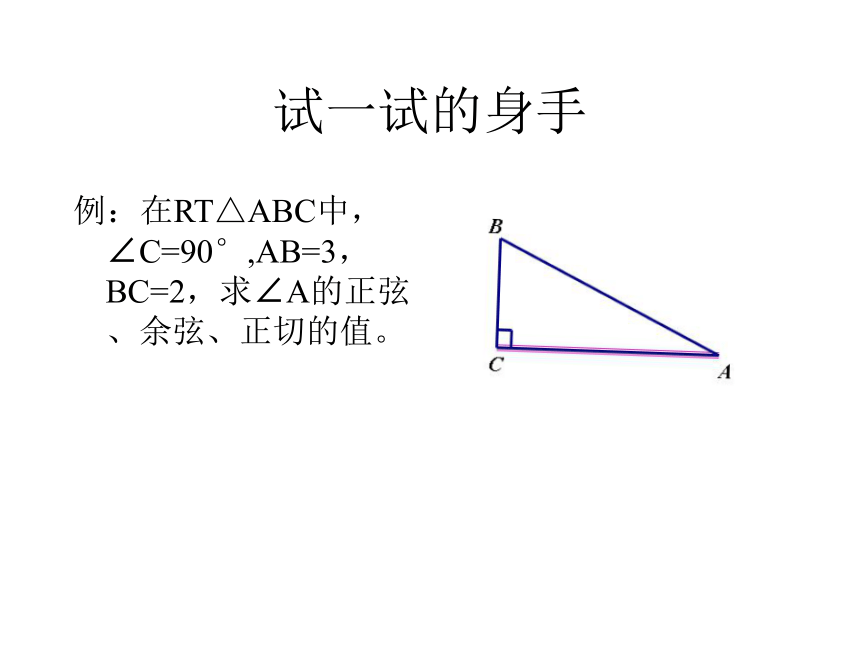
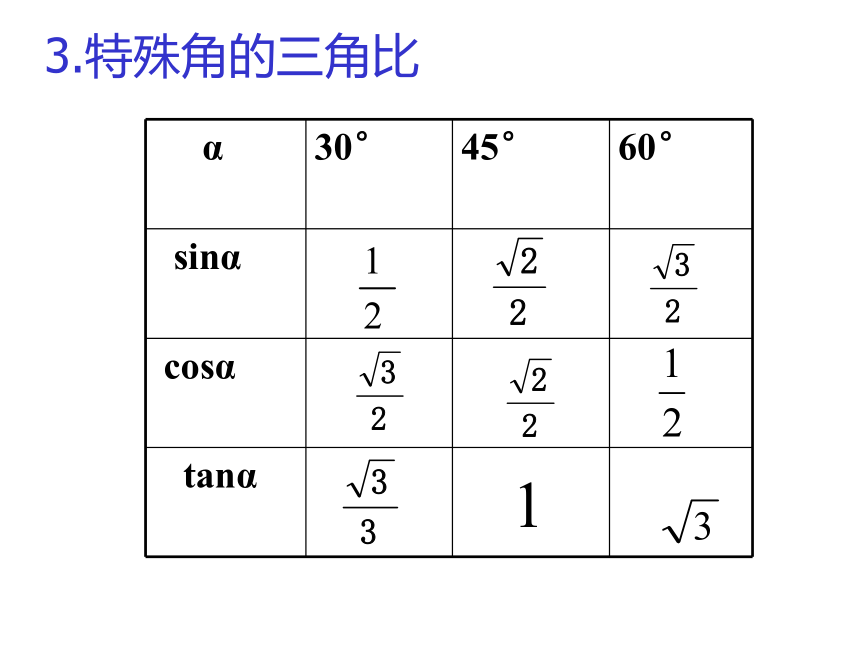
试一试的身手例：在RT△ABC中，∠C=90°,AB=3，BC=2，求∠A的正弦、余弦、正切的值。3.特殊角的三角比我能行例：求下列各式的值
（1）sin60°-3tan30°+2cos45°
(2)sin60°·cos60°+sin45°·cos45°-sin30°·cos30°
(3)tan60°+9tan30°-1/2tan45°+sin30°
4.有关三角比的性质一、正弦、余弦、正切的范围0﹤sina﹤1,0﹤cosa﹤1,tana＞0二、正弦、余弦、正切的性质（1）增减性：正弦和正切的值随着角度的增大而增大，余弦的值随着角度的增大而减小。（2）同角正弦、余弦、正切的关系：sin2a+cos2a=1,tana=(3)互余两角的三角比的关系：如果∠A+∠B=90°,那么sinA=cosB,cosA=sinB,tanA·tanB=1考考你1.若3tan(a+10°)= ,则锐角a的度数是2.当锐角A﹥45°时，sinA的取值范围是3.比较大小：sin37°,sin38°,con42°5、什么叫做解直角三角形？ 两个元素(至少一个是边)：两条边或一边一角
由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。
如果知道直角三角形的几个元素就可以求其他的元素？有几种情况？
三边之间的关系：a2＋b2＝c2（勾股定理）两角之间的关系:∠ A＋ ∠ B＝ 90o边角之间的关系（锐角三角比）：sinA＝6.解直角三角形的依据 在Rt△ABC中,∠C=900,a,b,c 分别是∠A,∠B,∠C 的对边.(1)已知a=3,b=3,求∠A;
(2)已知c=8,b=4,求a及∠A;
(3)已知c=8,∠A=450,求a及b .7.解直角三角形在实际问题中的应用:
仰角, 俯角 俯角 仰角水平线铅垂线坡度 :铅直高度 h 与水平宽度 l 的比,叫做坡度,
记做: i = h / l
坡度 i 是坡角α的正切,
即 i=tanαi = h / lh l α 山顶上有一旗杆，在地面上一点A处 测得杆顶B的仰角α =600，杆底C的仰角β =300，已知旗杆高BC=20米，求山高CD。典型习题2解:设AD=xm,
在Rt△ADC中， CD=AD?tan∠CAD= x?tan30?,
在Rt△ADB中， BD=AD?tan60?= x?tan60?, ∵ BD-CD=BC,BC=20m ∴ x?tan60?- x?tan30?=20∴CD=x?tan30?=10(m)答:山高CD为10米.变式训练 ?计算:
(1)sin45°-cos60°+tan°;
(2)sin223°+cos223°-tan45°;
硕果累累 一路下来，我们学习了很多知识，也有了很多的新想法。你能谈谈自己的收获吗？说一说，让大家一起来分享。1 通过今天这节课，你学到了哪些知识？
2 有哪些地方需要特别注意？
课堂小结谢谢同学们的精彩表现再见谢谢老师的指导