4.2.1 等差数列1 课件 (共30张PPT)
文档属性
| 名称 | 4.2.1 等差数列1 课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
(第一课时)
4.2.1 等差数列
1.数列的定义:
按一定次序排列的一列数。
2.数列的通项公式:
数列 的第 项 与项数 之间的函数关系式,即 。
复习回顾
(1)1896年,雅典举行第一届现代奥运会,到2008年的北京奥运会已经是第29届奥运会。
1896,1900,1904,…,2008,2012,( )
你能预测出第31届奥运会的时间吗?
2016
相差4
情境导入
情境导入
(2)2000年女子举重4个体重级别:48,53,58,63.
(4)气温随高度的变化/km:28, 21.5, 15, 8.5, 2 ,-4.5.
(3)各年末本利和(存100元):104.25, 108.5, 112.75, 117,121.25,……
8848.86m
单利:本利和=本金×(1+利率×存期)
利率:4.25%
问题探究1
(1)2008,2012,2016.
(2)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(3)104.25, 108.5, 112.75, 117,121.25,……
问题1:(1)以上数列有什么共同点?
对于数列(1),从第2项起,每一项与前一项的差都等于
对于数列(2),从第2项起,每一项与前一项的差都等于
对于数列(3),从第2项起,每一项与前一项的差都等于
对于数列(4),从第2项起,每一项与前一项的差都等于
4
4.25
-6.5
等差数列
(2)你能归纳出等差数列的定义吗?
什么是等差数列?
5
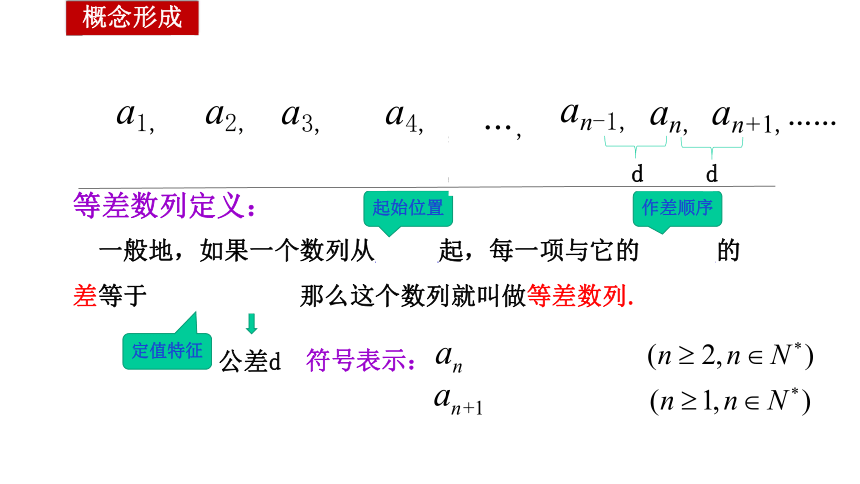
概念形成
等差数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
公差d
符号表示:
起始位置
作差顺序
定值特征
(1)2008, 2012, 2016.
(2)48, 53, 58, 63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(3)104.25, 108.5, 112.75, 117,121.25
a1,
a2,
a3,
a4,
an-1,
an,
an+1,……
…,
d
d
说一说
活动:寻找身边的等差数列
19,23,27,31
2006, 2010, 2014, 2018,
2022
概念辨析
1.判断以下数列是等差数列吗?
公差是3
(3)1,1,1,1,1;
公差是0
(2)6,4,2;
公差是-2
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
d>0 增数列
d<0 减数列
d=0 常数列
总结:可以利用等差数列定义判断一个数列
是否为等差数列.
是
是
是
不是
概念形成
(3)1,1,1,1,1;
(2)6,4,2;
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
(1)2008,2012,2016.
(3)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(2)104.25, 108.5, 112.75, 117,121.25……
由三个数a,A,b组成的等差数列
特点:
由三个数构成
a与b的等差中项.
概念形成
(2)6,4,2;
(1)2008,2012,2016;
由三个数a,A,b组成的等差数列,A为
特点:
由三个数构成
a与b的等差中项.
试一试:在横线填入一个数,让数列成为一个等差数列
(1)2, ,4;(2)-8, ,0;(3)a, ,b
-4, -1, 2, 5, 8,……
问题探究2
如何求等差数列的通项公式?
问题2:如何求an ?
a2= -4 + 1×3
a3= -4 + 2×3
a4= -4 + 3×3
a1= -4
3
3
3
3
……
a1
d
a1 , a2 , a3 , a4, a5…, an, …
d
d
d
d
观察
归纳
所以
由此得到:
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
问题探究2
由此得到:
(通项公式)
分析2:根据等差数列的定义:
累加法
问题探究2
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,
即知三求一 .
等差数列的通项公式:
知识归纳
解:∵
例题精讲
例1.(1)求等差数列8,5,2,…的第20项;
a20= -49
知三求一
例题精讲
例1.(2)判断-401是不是等差数列–5,-9 ,-13…的项
如果是,是第几项,如果不是,说明理由。
∵
即 -401是数列的第100项。
解:
说明:判断一个数是否为数列的项,只需令通项公式等于这个数,得到关于n的方程。若方程有正整数解,则它就是,否则不是。
知三求一方程思想
1. 求等差数列3,7,11,… …的第4,7,10项;
2. -20是不是等差数列 0,- ,-7, … …中的项;
小试牛刀
解:由等差数列通项公式
解得:
an=a1+(n-1)d
得:
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
例题精讲
例2.
例题精讲
例3.《孙子算经》是我国古代的数学名著,书
中有如下问题:“今五等诸侯,共分橘六
十,人别加三颗,五人各几何?”
6,9,12,15,18
意思为
“有5个人分60个橘子,他们分得的橘子数
成公差为3的等差数列,问5人各得多少橘
子?”
解:
1.已知等差数列{an}的首项a1=2,公差d=3,则数列{an}的通项公式为( )
A.an=3n-1 B.an=2n C.an=2n+3 D.an=3n+2
2.等差数列的第3项是7,第7项是-1,则它的第5项是________
课堂检测
A
3
3.地面到10km高空气温随高度的变化成等差数列:
高度/km 1 2 3 4 …… 9
气温/ 21.5 15 8.5 2 …… ?
-30.5
4.在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
1682,1758,1834,1910,1986,
你能预测出下一次哈雷彗星出现的大致时间吗?
2062
课堂检测
(1)两个定义:等差数列;等差中项
(2)两个公式:
(3)两种方法:归纳法;累加法
(4)两种思想:化归思想;方程思想.
课堂小结
再会!
-4, -1, 2, 5, 8,……
问题探究2
如何求等差数列的通项公式?
问题2:如何求an ?
a2= -4 + 1×3
a3= -4 + 2×3
a4= -4 + 3×3
a1= -4
3
3
3
3
……
a1
d
a1 , a2 , a3 , a4, a5…, an, …
d
d
d
d
观察
归纳
不完全归纳
(通项公式)
由此得到:
……
分析1:
课本作业:(基础题)40页 1,3,4,5题
(探究题)已知等差数列{an}的公差为d
求证:
实践作业:寻找生活中的等差数列,了解数学在生
活中的应用
课后作业
探究:已知等差数列{ }中,公差为d,则 与 (n , m ∈ N*) 有什么关系?
解:由等差数列的通项公式知
①-②
①
②
(这是等差数列通项公式的推广形式 )
小试牛刀
在等差数列{an}中
(1)已知a1=2,d =3,n =10,求an;
(2)已知a1=3,an=21,d =2,求n;
(3)已知d =1,a7=14,求a1;
(4)已知a1=2,a6=12,求d.
an=29
n =10
a1=8
d =2
知三求一方程思想
《张丘建算经》约成书于公元466-485年间,共三卷93题,包括测量、纺织、交换、纳税、冶炼、土木工程、利息等各方面的计算问题。其体例为问答式,条理精密,文词古雅,是中国古代数学史上的杰作,也是世界数学资料库中的一份宝贵的遗产。后世学者北周甄鸾、唐李淳风相继为该书做了注释。特别是唐代,经太史令李淳风注释整理,收入《算经十书》,成为当时算学馆先生的必读书目。《张丘建算经》现传本有92问,比较突出的成就有最大公约数与最小公倍数的计算,各种等差数列问题的解决、某些不定方程问题求解等。
现卷上第22题为“今有女善织,日益功急”即从第二天开始,每一天比前一天多织相同多的布,第一天织5尺,现在一月(按30天算)共织390尺,则从第二天开始,每天比前一天多织几尺布?
拓展延伸
观察可能导致发现,观察将揭示某种规律、模式或定理。
---波利亚
送给同学们的话
学习目标
1、能通过具体实例,发现数列的等差关系,理解等差数列的概念,会用定义判断一个数列是否为等差数列;
2、了解等差数列的通项公式的推导过程及思想,会求等差数列中的公差及通项公式;
3、体会用化归思想与方程思想解决问题.
(第一课时)
4.2.1 等差数列
1.数列的定义:
按一定次序排列的一列数。
2.数列的通项公式:
数列 的第 项 与项数 之间的函数关系式,即 。
复习回顾
(1)1896年,雅典举行第一届现代奥运会,到2008年的北京奥运会已经是第29届奥运会。
1896,1900,1904,…,2008,2012,( )
你能预测出第31届奥运会的时间吗?
2016
相差4
情境导入
情境导入
(2)2000年女子举重4个体重级别:48,53,58,63.
(4)气温随高度的变化/km:28, 21.5, 15, 8.5, 2 ,-4.5.
(3)各年末本利和(存100元):104.25, 108.5, 112.75, 117,121.25,……
8848.86m
单利:本利和=本金×(1+利率×存期)
利率:4.25%
问题探究1
(1)2008,2012,2016.
(2)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(3)104.25, 108.5, 112.75, 117,121.25,……
问题1:(1)以上数列有什么共同点?
对于数列(1),从第2项起,每一项与前一项的差都等于
对于数列(2),从第2项起,每一项与前一项的差都等于
对于数列(3),从第2项起,每一项与前一项的差都等于
对于数列(4),从第2项起,每一项与前一项的差都等于
4
4.25
-6.5
等差数列
(2)你能归纳出等差数列的定义吗?
什么是等差数列?
5
概念形成
等差数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
公差d
符号表示:
起始位置
作差顺序
定值特征
(1)2008, 2012, 2016.
(2)48, 53, 58, 63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(3)104.25, 108.5, 112.75, 117,121.25
a1,
a2,
a3,
a4,
an-1,
an,
an+1,……
…,
d
d
说一说
活动:寻找身边的等差数列
19,23,27,31
2006, 2010, 2014, 2018,
2022
概念辨析
1.判断以下数列是等差数列吗?
公差是3
(3)1,1,1,1,1;
公差是0
(2)6,4,2;
公差是-2
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
d>0 增数列
d<0 减数列
d=0 常数列
总结:可以利用等差数列定义判断一个数列
是否为等差数列.
是
是
是
不是
概念形成
(3)1,1,1,1,1;
(2)6,4,2;
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
(1)2008,2012,2016.
(3)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(2)104.25, 108.5, 112.75, 117,121.25……
由三个数a,A,b组成的等差数列
特点:
由三个数构成
a与b的等差中项.
概念形成
(2)6,4,2;
(1)2008,2012,2016;
由三个数a,A,b组成的等差数列,A为
特点:
由三个数构成
a与b的等差中项.
试一试:在横线填入一个数,让数列成为一个等差数列
(1)2, ,4;(2)-8, ,0;(3)a, ,b
-4, -1, 2, 5, 8,……
问题探究2
如何求等差数列的通项公式?
问题2:如何求an ?
a2= -4 + 1×3
a3= -4 + 2×3
a4= -4 + 3×3
a1= -4
3
3
3
3
……
a1
d
a1 , a2 , a3 , a4, a5…, an, …
d
d
d
d
观察
归纳
所以
由此得到:
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
问题探究2
由此得到:
(通项公式)
分析2:根据等差数列的定义:
累加法
问题探究2
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,
即知三求一 .
等差数列的通项公式:
知识归纳
解:∵
例题精讲
例1.(1)求等差数列8,5,2,…的第20项;
a20= -49
知三求一
例题精讲
例1.(2)判断-401是不是等差数列–5,-9 ,-13…的项
如果是,是第几项,如果不是,说明理由。
∵
即 -401是数列的第100项。
解:
说明:判断一个数是否为数列的项,只需令通项公式等于这个数,得到关于n的方程。若方程有正整数解,则它就是,否则不是。
知三求一方程思想
1. 求等差数列3,7,11,… …的第4,7,10项;
2. -20是不是等差数列 0,- ,-7, … …中的项;
小试牛刀
解:由等差数列通项公式
解得:
an=a1+(n-1)d
得:
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
例题精讲
例2.
例题精讲
例3.《孙子算经》是我国古代的数学名著,书
中有如下问题:“今五等诸侯,共分橘六
十,人别加三颗,五人各几何?”
6,9,12,15,18
意思为
“有5个人分60个橘子,他们分得的橘子数
成公差为3的等差数列,问5人各得多少橘
子?”
解:
1.已知等差数列{an}的首项a1=2,公差d=3,则数列{an}的通项公式为( )
A.an=3n-1 B.an=2n C.an=2n+3 D.an=3n+2
2.等差数列的第3项是7,第7项是-1,则它的第5项是________
课堂检测
A
3
3.地面到10km高空气温随高度的变化成等差数列:
高度/km 1 2 3 4 …… 9
气温/ 21.5 15 8.5 2 …… ?
-30.5
4.在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
1682,1758,1834,1910,1986,
你能预测出下一次哈雷彗星出现的大致时间吗?
2062
课堂检测
(1)两个定义:等差数列;等差中项
(2)两个公式:
(3)两种方法:归纳法;累加法
(4)两种思想:化归思想;方程思想.
课堂小结
再会!
-4, -1, 2, 5, 8,……
问题探究2
如何求等差数列的通项公式?
问题2:如何求an ?
a2= -4 + 1×3
a3= -4 + 2×3
a4= -4 + 3×3
a1= -4
3
3
3
3
……
a1
d
a1 , a2 , a3 , a4, a5…, an, …
d
d
d
d
观察
归纳
不完全归纳
(通项公式)
由此得到:
……
分析1:
课本作业:(基础题)40页 1,3,4,5题
(探究题)已知等差数列{an}的公差为d
求证:
实践作业:寻找生活中的等差数列,了解数学在生
活中的应用
课后作业
探究:已知等差数列{ }中,公差为d,则 与 (n , m ∈ N*) 有什么关系?
解:由等差数列的通项公式知
①-②
①
②
(这是等差数列通项公式的推广形式 )
小试牛刀
在等差数列{an}中
(1)已知a1=2,d =3,n =10,求an;
(2)已知a1=3,an=21,d =2,求n;
(3)已知d =1,a7=14,求a1;
(4)已知a1=2,a6=12,求d.
an=29
n =10
a1=8
d =2
知三求一方程思想
《张丘建算经》约成书于公元466-485年间,共三卷93题,包括测量、纺织、交换、纳税、冶炼、土木工程、利息等各方面的计算问题。其体例为问答式,条理精密,文词古雅,是中国古代数学史上的杰作,也是世界数学资料库中的一份宝贵的遗产。后世学者北周甄鸾、唐李淳风相继为该书做了注释。特别是唐代,经太史令李淳风注释整理,收入《算经十书》,成为当时算学馆先生的必读书目。《张丘建算经》现传本有92问,比较突出的成就有最大公约数与最小公倍数的计算,各种等差数列问题的解决、某些不定方程问题求解等。
现卷上第22题为“今有女善织,日益功急”即从第二天开始,每一天比前一天多织相同多的布,第一天织5尺,现在一月(按30天算)共织390尺,则从第二天开始,每天比前一天多织几尺布?
拓展延伸
观察可能导致发现,观察将揭示某种规律、模式或定理。
---波利亚
送给同学们的话
学习目标
1、能通过具体实例,发现数列的等差关系,理解等差数列的概念,会用定义判断一个数列是否为等差数列;
2、了解等差数列的通项公式的推导过程及思想,会求等差数列中的公差及通项公式;
3、体会用化归思想与方程思想解决问题.
