5.3.2 函数的极值与最大(小)值1 课件 (共22张PPT)
文档属性
| 名称 | 5.3.2 函数的极值与最大(小)值1 课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 820.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 10:19:14 | ||
图片预览




文档简介
(共22张PPT)
函数的极值(第一课时)
5.3.2 函数的极值与最大(小)值
情境引入
结合苏轼在《题西林壁》中的诗句“横看成岭侧成峰,远近高低各不同”,描述的是庐山的连绵起伏。由此联想庐山的连绵起伏形成好多的“峰点”与“谷点”.这就象数学上要研究的函数的极值.
问题1 观察庐山连绵起伏的图片,思考山势有什么特点?
图 1
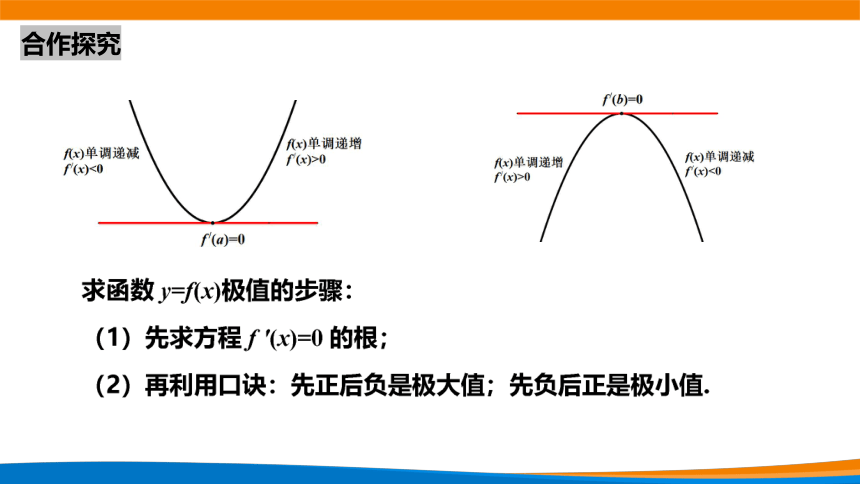
合作探究
图 2 图 3
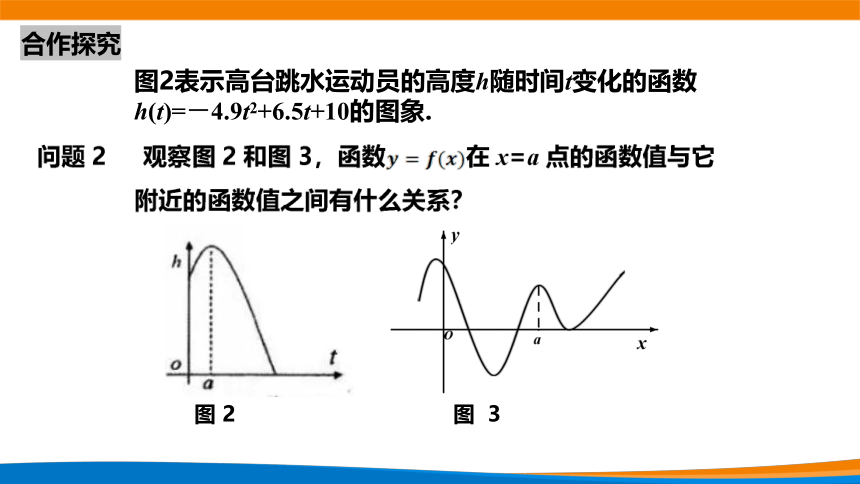
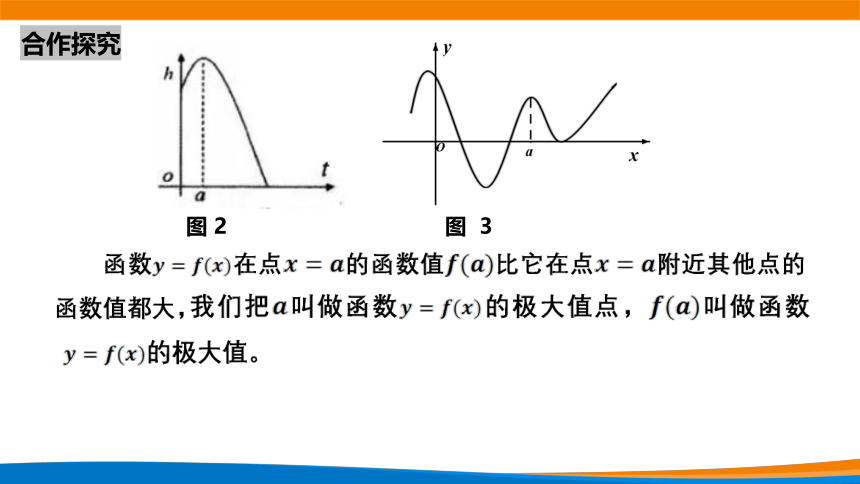
图2表示高台跳水运动员的高度h随时间t变化的函数
h(t)=-4.9t2+6.5t+10的图象.
合作探究
图 2 图 3
合作探究
极小值点、极大值点统称为极值点, 极小值、极大值统称为极值.
合作探究
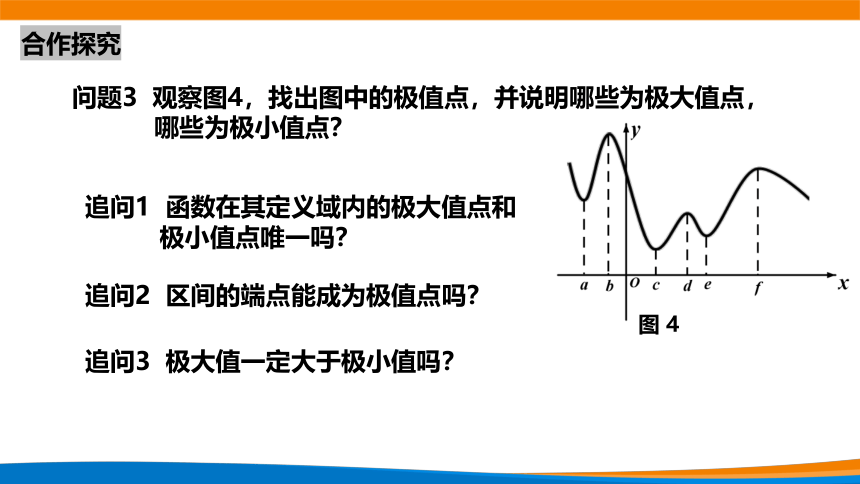
问题3 观察图4,找出图中的极值点,并说明哪些为极大值点,
哪些为极小值点?
追问1 函数在其定义域内的极大值点和
极小值点唯一吗?
追问2 区间的端点能成为极值点吗?
追问3 极大值一定大于极小值吗?
图 4
合作探究
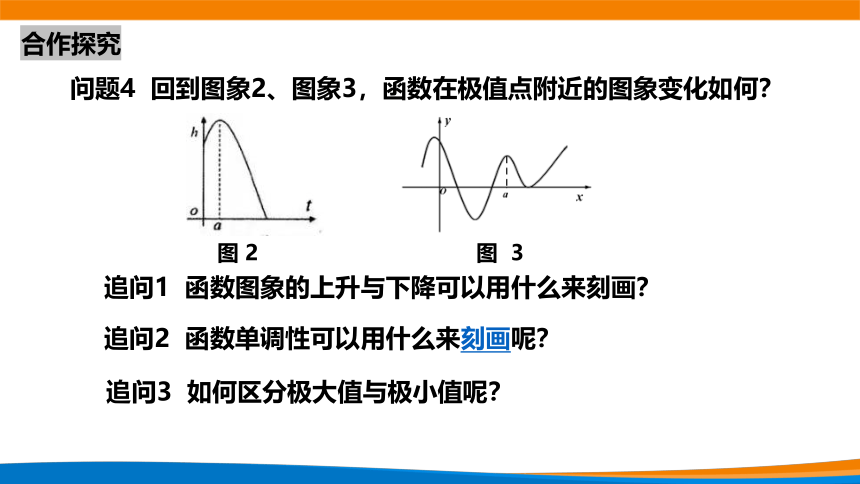
问题4 回到图象2、图象3,函数在极值点附近的图象变化如何?
图 2 图 3
追问1 函数图象的上升与下降可以用什么来刻画?
追问2 函数单调性可以用什么来刻画呢?
追问3 如何区分极大值与极小值呢?
合作探究
学以致用
例1.求函数的极值.
学以致用
x 2
+
+
0
0
单调递增
单调递增
单调递减
学以致用
学以致用
学以致用
追问:导数值为0的点一定是函数的极值点吗?
导数值为0的点不一定是函数的极值点.
函数
时,
时,
在上是增函数,
0不是函数的极值点.
学以致用
追问:导数值为0的点一定是函数的极值点吗?
学以致用
学以致用
学以致用
解:是函数的极值点.
其中,是极大值点, 是极小值点.
学以致用
追问:函数的极大值点和极小值点分别是什么?
解:是函数的极大值点,
是函数的极小值点.
分析:根据极大值点和极小值点的定义进行判断.
课堂小结
的单调性
的正负性
的极值点
的零点
导数的工具性作用
注意判断零点附近
的正负性
数形结合、化归转化
课后作业
课后作业
再会!
函数的极值(第一课时)
5.3.2 函数的极值与最大(小)值
情境引入
结合苏轼在《题西林壁》中的诗句“横看成岭侧成峰,远近高低各不同”,描述的是庐山的连绵起伏。由此联想庐山的连绵起伏形成好多的“峰点”与“谷点”.这就象数学上要研究的函数的极值.
问题1 观察庐山连绵起伏的图片,思考山势有什么特点?
图 1
合作探究
图 2 图 3
图2表示高台跳水运动员的高度h随时间t变化的函数
h(t)=-4.9t2+6.5t+10的图象.
合作探究
图 2 图 3
合作探究
极小值点、极大值点统称为极值点, 极小值、极大值统称为极值.
合作探究
问题3 观察图4,找出图中的极值点,并说明哪些为极大值点,
哪些为极小值点?
追问1 函数在其定义域内的极大值点和
极小值点唯一吗?
追问2 区间的端点能成为极值点吗?
追问3 极大值一定大于极小值吗?
图 4
合作探究
问题4 回到图象2、图象3,函数在极值点附近的图象变化如何?
图 2 图 3
追问1 函数图象的上升与下降可以用什么来刻画?
追问2 函数单调性可以用什么来刻画呢?
追问3 如何区分极大值与极小值呢?
合作探究
学以致用
例1.求函数的极值.
学以致用
x 2
+
+
0
0
单调递增
单调递增
单调递减
学以致用
学以致用
学以致用
追问:导数值为0的点一定是函数的极值点吗?
导数值为0的点不一定是函数的极值点.
函数
时,
时,
在上是增函数,
0不是函数的极值点.
学以致用
追问:导数值为0的点一定是函数的极值点吗?
学以致用
学以致用
学以致用
解:是函数的极值点.
其中,是极大值点, 是极小值点.
学以致用
追问:函数的极大值点和极小值点分别是什么?
解:是函数的极大值点,
是函数的极小值点.
分析:根据极大值点和极小值点的定义进行判断.
课堂小结
的单调性
的正负性
的极值点
的零点
导数的工具性作用
注意判断零点附近
的正负性
数形结合、化归转化
课后作业
课后作业
再会!
