函数的单调性与导数 课件 (共25张PPT)
文档属性
| 名称 | 函数的单调性与导数 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
函数的单调性
与导数
1
创设情境
10米高台跳水
1
创设情境
1
创设情境
活动一:小组讨论,填写下面学习任务单
单调递增
单调递减
>0
<0
单调递增
单调递减
1
创设情境
思考:你能从上述两个图形中发现函数的单调性与函数导数的正负有什么关系吗?
1
创设情境
结论
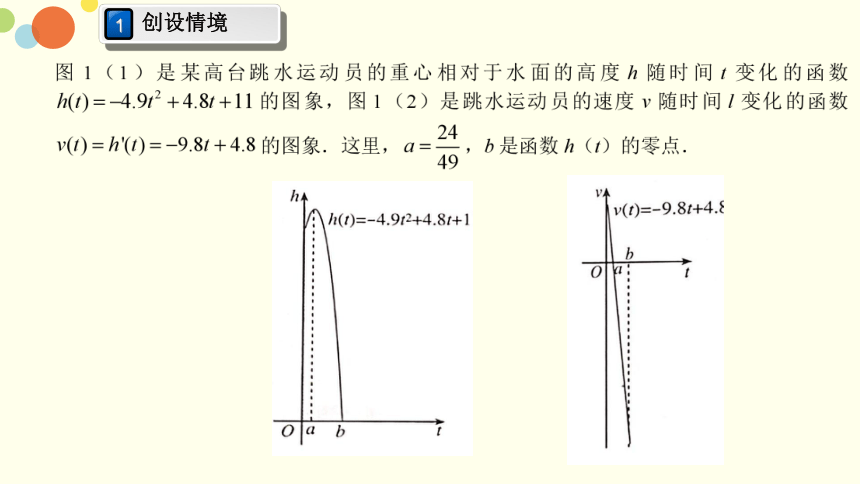
当t∈(0,a)时,h'(t)>0,函数h(t)的图像是“上升”的,函数h(t)在(0,a)内单调递增的;
当t∈(a,b)时,h'(t)<0,函数h(t)的图像是“下降”的,函数h(t)在(a,b)内单调递减的.
活动二:绘制一些函数的图象,验证你的猜想是否成立
2
探究新知
2
探究新知
2
探究新知
a
y
x
0
.
.
.
.
.
.
.
观察函数y=f(x) 的图象:
总结:
在区间(-∞,a)上,切线斜率小于0,即导数小于0,这时函数单调递减;
在区间(a,+∞)上,切线斜率大于0,即导数大于0,这时函数单调递增.
2
探究新知
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
如果在某个区间内恒有f ′(x)=0, 则f(x)为常数.
3
生成概念
4
学以致用
f(x)=x3+3x
O
y
x
4
学以致用
f(x)=x3+3x
O
y
x
4
学以致用
4
学以致用
利用导数讨论函数单调性的步骤:
4
学以致用
4
学以致用
O
1
4
x
y
y=f(x)
4
学以致用
增减有快慢之分图象有陡缓之别;那么这跟导数又有什么关系呢?
思考:观察两种画法,你认为这两个图的区别在哪?
4
学以致用
4
学以致用
4
学以致用
4
学以致用
4
学以致用
思考:由例4可以得到什么结论?
知识层面
学习反思
本节课你学到了什么知识?
你是如何获得这些知识的?
本节课你有什么体会?
5
归纳小结
谢谢聆听!
函数的单调性
与导数
1
创设情境
10米高台跳水
1
创设情境
1
创设情境
活动一:小组讨论,填写下面学习任务单
单调递增
单调递减
>0
<0
单调递增
单调递减
1
创设情境
思考:你能从上述两个图形中发现函数的单调性与函数导数的正负有什么关系吗?
1
创设情境
结论
当t∈(0,a)时,h'(t)>0,函数h(t)的图像是“上升”的,函数h(t)在(0,a)内单调递增的;
当t∈(a,b)时,h'(t)<0,函数h(t)的图像是“下降”的,函数h(t)在(a,b)内单调递减的.
活动二:绘制一些函数的图象,验证你的猜想是否成立
2
探究新知
2
探究新知
2
探究新知
a
y
x
0
.
.
.
.
.
.
.
观察函数y=f(x) 的图象:
总结:
在区间(-∞,a)上,切线斜率小于0,即导数小于0,这时函数单调递减;
在区间(a,+∞)上,切线斜率大于0,即导数大于0,这时函数单调递增.
2
探究新知
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
如果在某个区间内恒有f ′(x)=0, 则f(x)为常数.
3
生成概念
4
学以致用
f(x)=x3+3x
O
y
x
4
学以致用
f(x)=x3+3x
O
y
x
4
学以致用
4
学以致用
利用导数讨论函数单调性的步骤:
4
学以致用
4
学以致用
O
1
4
x
y
y=f(x)
4
学以致用
增减有快慢之分图象有陡缓之别;那么这跟导数又有什么关系呢?
思考:观察两种画法,你认为这两个图的区别在哪?
4
学以致用
4
学以致用
4
学以致用
4
学以致用
4
学以致用
思考:由例4可以得到什么结论?
知识层面
学习反思
本节课你学到了什么知识?
你是如何获得这些知识的?
本节课你有什么体会?
5
归纳小结
谢谢聆听!
