北师大版数学九年级下册 3.5 确定圆的条件 课件(共20张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 3.5 确定圆的条件 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 279.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-04 22:00:58 | ||
图片预览






文档简介
(共20张PPT)
第3章 圆
3.5 确定圆的条件
设置情境,提出问题
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
启发思路,分析问题
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
这个实际问题若从数学角度去观察分析,你认为可转化为什么问题?
启发思路,分析问题
要画一个圆,必须知道什么?
要知道这个圆的圆心和半径.
过一个已知点A如何作圆?圆心在哪里?半径呢?这样的圆可以作多少个?
启发思路,分析问题
过一个已知点A如何作圆?圆心在哪里?半径呢?这样的圆可以作多少个?
经过一点可以作________直线,经过两点可以作________直线.
无数条
一条
那么经过一点能作圆吗?能作几个?经过两点呢?
启发思路,分析问题
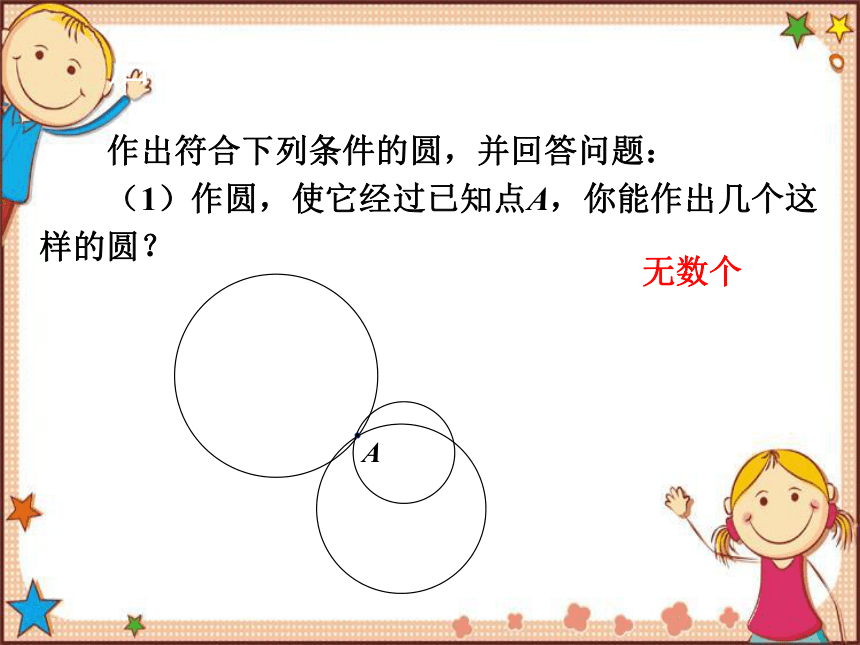
作出符合下列条件的圆,并回答问题:
(1)作圆,使它经过已知点A,你能作出几个这样的圆?
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几个这样的圆?其圆心的位置有什么特点?与线段AB有何关系?为什么?
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一条直线上).你是如何做的?你能作出几个这样的圆?
启发思路,分析问题
作出符合下列条件的圆,并回答问题:
(1)作圆,使它经过已知点A,你能作出几个这样的圆?
A
无数个
启发思路,分析问题
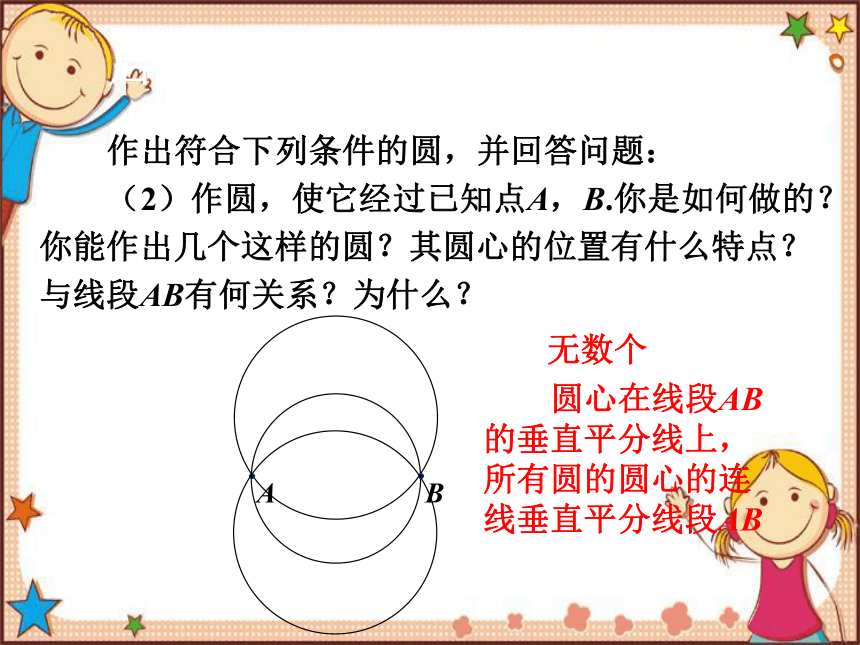
作出符合下列条件的圆,并回答问题:
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几个这样的圆?其圆心的位置有什么特点?与线段AB有何关系?为什么?
A
B
无数个
圆心在线段AB的垂直平分线上,所有圆的圆心的连线垂直平分线段AB
启发思路,分析问题
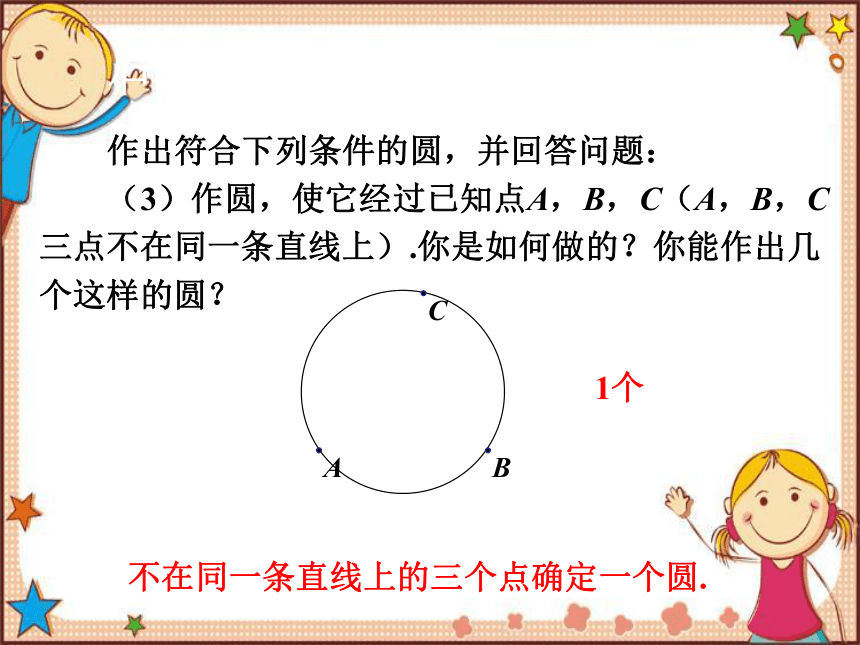
作出符合下列条件的圆,并回答问题:
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一条直线上).你是如何做的?你能作出几个这样的圆?
A
B
C
1个
不在同一条直线上的三个点确定一个圆.
引导解答,解决问题
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
想一想:三角形的外心是否一定在三角形内?
对三角形的形状分类讨论
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
锐角三角形的外心在它的内部;
直角三角形的斜边是它外接圆的直径,外心即为斜边的中点;
钝角三角形的外心在其外部.
强化训练,消化新知
1.如图,⊙O是△ABC的________圆,圆心O是三角形的________心,它是_______________线的交点,到三角形_______________距离相等.
O
A
B
C
外接
外
三边垂直平分
三个顶点
强化训练,消化新知
2.下列命题中正确的有几个?
(1)每个三角形都只有一个外心.
(2)三角形的外心到三角形各边的距离相等.
(3)四边形不一定有外接圆.
(4)三点确定一个圆.
√
×
√
×
解决疑问
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
只需要把这块残片拿到玻璃店即可,因为不在一条直线上的三点确定一个圆.
1.通过本课学习,知道了根据什么条件可以确定一个圆?
任何一个三角形都可以确定一个圆,它称为三角形的外接圆,这个圆心是三角形的外心.它有哪些性质?它一定在三角形的外部吗?
2.过矩形的四个顶点能作圆吗?圆心在哪里?经过不在同一条直线上的任意四点能作圆吗?
师生小结,形成知识体系
1.教材第87~88页习题3.6第1~4题.
2.车间工人要将一个破损的圆盘复原,你有办法吗?
布置作业
谢谢大家!
再见!
第3章 圆
3.5 确定圆的条件
设置情境,提出问题
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
启发思路,分析问题
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
这个实际问题若从数学角度去观察分析,你认为可转化为什么问题?
启发思路,分析问题
要画一个圆,必须知道什么?
要知道这个圆的圆心和半径.
过一个已知点A如何作圆?圆心在哪里?半径呢?这样的圆可以作多少个?
启发思路,分析问题
过一个已知点A如何作圆?圆心在哪里?半径呢?这样的圆可以作多少个?
经过一点可以作________直线,经过两点可以作________直线.
无数条
一条
那么经过一点能作圆吗?能作几个?经过两点呢?
启发思路,分析问题
作出符合下列条件的圆,并回答问题:
(1)作圆,使它经过已知点A,你能作出几个这样的圆?
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几个这样的圆?其圆心的位置有什么特点?与线段AB有何关系?为什么?
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一条直线上).你是如何做的?你能作出几个这样的圆?
启发思路,分析问题
作出符合下列条件的圆,并回答问题:
(1)作圆,使它经过已知点A,你能作出几个这样的圆?
A
无数个
启发思路,分析问题
作出符合下列条件的圆,并回答问题:
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几个这样的圆?其圆心的位置有什么特点?与线段AB有何关系?为什么?
A
B
无数个
圆心在线段AB的垂直平分线上,所有圆的圆心的连线垂直平分线段AB
启发思路,分析问题
作出符合下列条件的圆,并回答问题:
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一条直线上).你是如何做的?你能作出几个这样的圆?
A
B
C
1个
不在同一条直线上的三个点确定一个圆.
引导解答,解决问题
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
想一想:三角形的外心是否一定在三角形内?
对三角形的形状分类讨论
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
想一想:三角形的外心是否一定在三角形内?
A
B
C
引导解答,解决问题
锐角三角形的外心在它的内部;
直角三角形的斜边是它外接圆的直径,外心即为斜边的中点;
钝角三角形的外心在其外部.
强化训练,消化新知
1.如图,⊙O是△ABC的________圆,圆心O是三角形的________心,它是_______________线的交点,到三角形_______________距离相等.
O
A
B
C
外接
外
三边垂直平分
三个顶点
强化训练,消化新知
2.下列命题中正确的有几个?
(1)每个三角形都只有一个外心.
(2)三角形的外心到三角形各边的距离相等.
(3)四边形不一定有外接圆.
(4)三点确定一个圆.
√
×
√
×
解决疑问
小明家有一块已被打碎的圆形玻璃镜子,现欲重新配制一块圆玻璃片,小明准备把碎玻璃片连同这块残片一起拿到玻璃店,这样行吗?你会采用什么方法?
只需要把这块残片拿到玻璃店即可,因为不在一条直线上的三点确定一个圆.
1.通过本课学习,知道了根据什么条件可以确定一个圆?
任何一个三角形都可以确定一个圆,它称为三角形的外接圆,这个圆心是三角形的外心.它有哪些性质?它一定在三角形的外部吗?
2.过矩形的四个顶点能作圆吗?圆心在哪里?经过不在同一条直线上的任意四点能作圆吗?
师生小结,形成知识体系
1.教材第87~88页习题3.6第1~4题.
2.车间工人要将一个破损的圆盘复原,你有办法吗?
布置作业
谢谢大家!
再见!
